C++一本通基础算法：广度优先搜索（BFS）

tip：该算法将会疯狂使用队列，包括各种类型的队列

算法概述：先将起点入队，先向起点相邻的位置检索，如果满足条件，那么将这个位置入队。 然后将起点出队。再将所有与队首相邻且满足条件的位置入队，队首出队，知道队列为空。

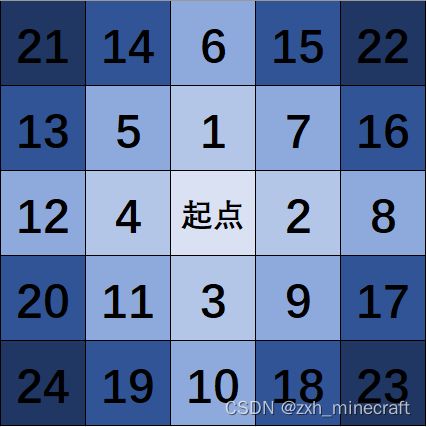
算法图像

 如图所示，从起点检索，将1,2,3,4分别入队，起点出队，现在队列的队首为1，检索1周围的位置，将5,6,7分别入队，1出队，现在队首为2，检索2周围的位置，将8,9入队，……。直到24为队首时，周围不存在任何一个位置可以入队，且24已经为队列中唯一的元素，24出队，此时队列为空，搜索结束。

算法特点：需要用到大量的队列操作，可以解决很多的搜索问题，在求解最短路径问题且两个相邻的位置距离一定时，最先搜索到终点的路径长度就是最短路径。

广度优先搜索代码的一般形式

void bfs (   ) {                     //参数由解题需求决定
	queue  q;                   //类型自定，大概率为结构体
	q.push();                        //起点入队
	                                 //标记当前位置，避免重复访问
	while (q.size()) {               //只要队不为空
		int t = q.front();           //取出队首元素
		q.pop();                     //队首出队
		for ( ; ; ) {                //循环用于检索队首的相邻位置
			int xx , yy;             
			if ( ) {                 //如果这个位置满足条件
				q.push();            //将这个位置入队
				                     //标记当前位置 
			}
		}
	} 
}

 题目链接

信息学奥赛一本通（C++版）在线评测系统 (ssoier.cn)

分析：遍历矩阵，如果发现矩形中某一个元素为细胞，则细胞总数加1，则运用广搜将与这个细胞所相邻的所有细胞（包括这个细胞）都找出来并设置为非细胞元素，继续遍历。

心得：这道题在输入时用的是getchar，不管怎么改最终只能通过一个点，后来发现cin也可以输入单个字符，将getchar换成cin后，就可以通过了。

代码

#include 
#include 
#include 
using namespace std;

const int N = 10100;
int n,m,xy[4][2] = {1,0,0,1,-1,0,0,-1},ans = 0;
char a[N][N];

struct node {
	int x,y;
};

void bfs (int x,int y) {
	queue  q;
	q.push((node) {x,y});
	a[x][y] = '0';
	while (q.size()) {
	//	cout << q.front().x << " " << q.front().y << endl;
		node k = q.front();
		q.pop();
		for (int i = 0;i < 4;i++) {
			int xx = k.x + xy[i][0],yy = k.y + xy[i][1];
			if (xx >= 1 && xx <= n && yy >= 1 && yy <= m && a[xx][yy] != '0') {
			//	cout << xx << " b " << yy << endl;
				a[xx][yy] = '0';
				q.push((node){xx,yy});
			}
		}
	}
}

int main () {
	cin >> n >> m;
	getchar();
	for (int i = 1;i <= n;i++) {
		for (int j = 1;j <= m;j++) {
			cin >> a[i][j];
		//	cout << a[i][j] << endl;
		}
	}
	for (int i = 1;i <= n;i++) {
		for (int j = 1;j <= m;j++) {
			if (a[i][j] != '0') {
		//		cout << i << " " << j << endl;
				bfs(i,j);
				ans++;
			}
		}
	}
	cout << ans << endl;
	return 0;
}

题目链接

信息学奥赛一本通（C++版）在线评测系统 (ssoier.cn)

分析：经典的广搜走迷宫，设置4个偏移量再用广搜模板套即可。同时由于广搜是宽度优先，所以第一个搜索到的解即为最短路径解

心得：没什么好说的，一遍过。

#include 
#include 
#include 
using namespace std;

const int N = 25;
char a[N][N];
bool b[N][N];
int m,n,ans,sx,sy,ex,ey,xy[4][2]{1,0,0,1,-1,0,0,-1};

struct node {
	int x,y,cnt;
};

void bfs (int x,int y) {
//	cout << endl;
	queue  q;
	q.push((node){x,y,0});
	b[x][y] = 1;
	while (q.size()) {
		node t = q.front();
		if (t.x == ex && t.y == ey) {
			ans = t.cnt;
			return;
		}
		q.pop();
		for (int i = 0;i < 4;i++) {
			int xx = t.x + xy[i][0],yy = t.y + xy[i][1];
		//		cout << xx << " " << yy << endl;
			if (xx >= 1 && xx <= m && yy >= 1 && yy <= n && !b[xx][yy] && a[xx][yy] != '#') {
				b[xx][yy] = 1;
				q.push((node){xx,yy,t.cnt + 1});
			}
		}
	}
}

int main () {
	while (cin >> m >> n) {
		if (m == 0 && n == 0) break;
		memset(b,0,sizeof(b));
		ans = 0;
		for (int i = 1;i <= m;i++) {
			for (int j = 1;j <= n;j++) {
				cin >> a[i][j];
				if (a[i][j] == '@') {
					sx = i;
					sy = j;
				}
				if (a[i][j] == '*') {
					ex = i;
					ey = j;
				}
			}
		}
//		cout << sx << " " << sy << endl;
		bfs (sx,sy);
		if (ans == 0) cout << -1 << endl;
		else cout << ans << endl;
	}
	return 0;
}