【你哥电力电子】flyback电路，多路输出分析

FLYBACK电路

2023年7月12日
#elecEngeneer

---

---

又称反激式变换器。广泛应用于高压和离线供电电源，能做到恒功率输出，不需要输出电感，节省体积。升降压变换器：
$$V_o=\frac{N_s}{N_p}\cdot \frac{D}{1-D}{V}_i$$
$D$：占空比，$D\in (0,1)$，电压极性为正。$N_p$ 为原边绕组匝数，$N_s$ 为副边绕组匝数。

---

1. FLYBACK电路的基本原理

FLYBACK电路的工作过程不好理解，这里通过变压器给出解释。耦合电感的同名端由互感磁通的方向决定，从同名端流入的电流产生的互感磁通方向应相同。同时，变压器输入侧从同名端流入电流，输出侧也会从同名端流出电流。往耦合电感中间加入铁芯，可以提高耦合系数，互感几乎和自感相等，即得到了变压器。如果铁芯存在气隙，则由磁路的欧姆定律，磁位降大多集中在气隙部分，也就是气隙部分储存了磁场的能量。

如上图，电感两端电压可以突变，设输入侧加电压，输入侧产生从同名端流入的电流，磁通开始建立，输出边绕组为了抵抗磁通的建立会产生从同名端流出的电流。若设绕组从同名端流入的电流为正，则输入电流与输出电流反相。下面回到反激式变换器：

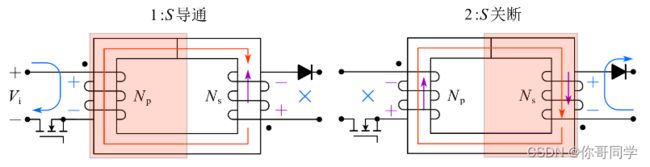
开关S导通时，输入侧原边绕组$N_p$在正向电压$V_i$作用下产生一个增加的正向电流$i_i$，正向电流产生磁场，磁场能量储存在气隙，由楞次定律，副边绕组产生抵御磁场增加的感应电动势（相当于电源），但二极管截住了电流，所以副边没有电流，能量没有传递。开关S关断时，原边绕组强制截流，电流为0，由于磁场不能突变，副边绕组产生抵御磁场减小的感应电动势，原边绕组也一样。此时变压器两端电压的极性与开关导通时相反，二极管导通，磁场能量传递到输出侧。
反激式变换器的能量是分步传递的，开关导通时储存能量，开关关断时传递能量。正激式变换器则在开关导通时传递能量。
反激式变换器与BUCK-BOOST电路很像，其实就是将BUCK-BOOST电路的电感拆开成变压器，并将原副边极性反转。

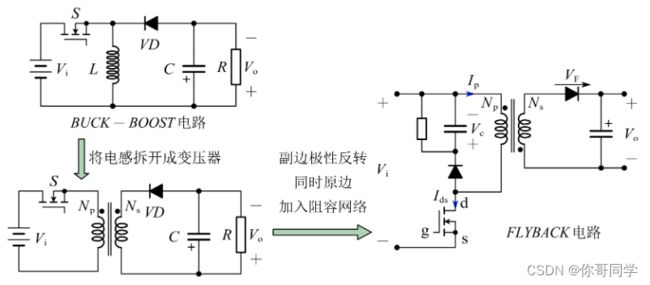
在开关管关断瞬间，原边剩余的电流给MOS管的结电容充电，导致开关管上有较大的尖峰电压，为了减小尖峰电压，原边加入了阻容网络，原边二极管提供了低阻值的通路，同时也阻挡了开关管关断时反射电压在阻容网络上形成回路。

FLYBACK多路输出时的分析

FLYBACK主要考虑的因素有副边二极管的导通压降与导通电阻。二极管导通电阻在重载时（电流大，等效负载电阻小）会分压，导致输出电压降低。在CCM时，由秒伏平衡有：
$$V_{i}D{T}_s=V_{oeqp}(1-D)T_s$$
$V_{oeqp}$ 为原边绕组在开关关断时的反射电压（感应电动势）。
$$V_{oeqp}=\frac{V_{i}D}{1-D}$$
再乘以匝数比可得到开关关断时副边绕组的电压：
$$V_{s(n)}=V_i\frac{D}{1-D}\frac{N_{s(n)}}{N_p}$$
副边绕组的电压减去二极管导通压降 $V_F$，由于有电容支撑，所以得到的居寺和副边的输出电压：
$$V_{o(n)}=V_i\frac{D}{1-D}\frac{N_{s(n)}}{N_p}-V_F$$
再考虑二极管导通电阻的分压，有：
$$V_{o(n)}=V_i\frac{D}{1-D}\frac{N_{s(n)}}{N_p}-V_F-\frac{V_{o(n)}}{R}\cdot \frac{R_F}{1-D}$$
$$V_{o(n)}=\frac{V_{s(n)}-V_F}{1+R_F/[R_{(n)}(1-D)]}$$
需要明确，对于每一路输出绕组而言，再电压上都有相同的关系，仅与原边反射变压与变比有关，变比确定，则占空比决定了副边电压。下面求多路输出下临界模式的占空比，由于电压的关系确定，所以可以从能量的角度得出输入电流：
$$V_i{I}_i=\sum _{i=1}^n(\frac{V_{o(i)}}{R_{(i)}}{)}^2(R_{(i)}+\frac{R_F}{1-D})$$
考虑了二极管导通电阻带来的损耗。而临界模式要求：
$$I_p>\frac{\Delta i_p}{2}=\frac{V_{i}D{T}_s}{2L_p}$$
$$I_p=\frac{I_i}{D}$$
通过联立这几个公式就可以解出占空比的范围。当然，直接手推非常麻烦，而占空比的取值仅在 $0$ 到 $1$ 之间，所以我们通过matlab编程求解。设有 $3$ 路输出，$V_i=300V$，$D=0.6$ ，$L_p=500\mu H$，$V_F=0.9V$，$R_F=0.3\Omega$，$f_{sw}=65000\text{Hz}$，原边绕组 $89$ 匝，副边绕组分别为 $13、19、6$ 匝，对应负载电阻 $7.5、1000、16.7$ 欧姆。

clc; clear
syms N_p N_s1 N_s2 N_s3
syms V_i R_1 R_2 R_3 R_F V_F I_i
syms D T_sw L_p

V_s1 = V_i*D/(1-D)*N_s1/N_p;
V_s2 = V_i*D/(1-D)*N_s2/N_p;
V_s3 = V_i*D/(1-D)*N_s3/N_p;

V_o1 = (V_s1-V_F)/(1+R_F/(R_1*(1-D)));
V_o2 = (V_s2-V_F)/(1+R_F/(R_2*(1-D)));
V_o3 = (V_s3-V_F)/(1+R_F/(R_3*(1-D)));
pretty(V_o1)
eq1 = (V_o1/R_1)^2*(R_1+R_F/(1-D))+(V_o2/R_2)^2*(R_2+R_F/(1-D))+...
    (V_o3/R_3)^2*(R_3+R_F/(1-D))-V_i*I_i;
[I_i] = solve(eq1, I_i);
I_i = simplify(I_i);
pretty(I_i)
I_i = subs(I_i, {N_p, N_s1, N_s2, N_s3, V_F, R_F, V_i}, {89, 13, 19, 6, 0.9, 0.3, 300});
I_i = subs(I_i, {R_1, R_2, R_3}, {7.5, 1000, 16.7}); % 代入数值
I_i = collect(I_i, D);
I_i
I_Lp = I_i/D;
delta_I_Lp = 300*D/500e-6/65000;

cond = I_Lp > delta_I_Lp/2;
for i = 0.001: 0.001: 0.999
    if subs(cond, D, i)
        disp(i)
    end
end

可以解得在 $0<D<0.007$ 与 $0.573<D<1$ 时为连续模式。

---

下链

---