查找算法 - 图文解析二分查找、插值查找、斐波拉契查找算法
查找算法
经典的查找算法有7种:
顺序查找,二分查找,插值查找,斐波那契查找,树表查找,分块查找,哈希查找
其中顺序查找没得说,就是简单的按照顺序从前往后查,一个for循环就解决了
这篇文章将解析二分查找、插值查找、斐波拉契查找,这三种查找算法其实都类似,只是优化了分段的方式
插值查找、斐波拉契查找是二分查找的优化
二分查找
二分查找算法概念
二分查找:顾名思义,要将查找的线性表分成两个线性表
用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功;若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到查找到或查找结束发现表中没有这样的结点
注意:二分查找需要线性表有序
例如:一个数组1,8,10,89,1000,20003,二分查找的步骤:
- 设置左指针left指向1(线性表最左边),右指针right指向20003(线性表最右边),传入查找值,例如1000
- 计算中间值
mid = (left + right) / 2,也就是2,指向10
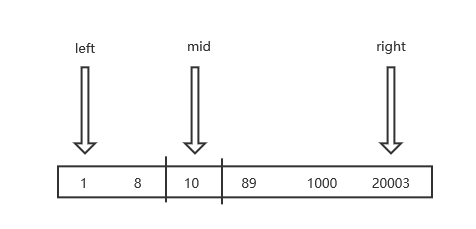
- 将线性表分为左右两段及中间值,判断查找值1000是大于、小于、等于中间值
- 现在大于中间值,即向右查找,递归上面的方法(移动指针)
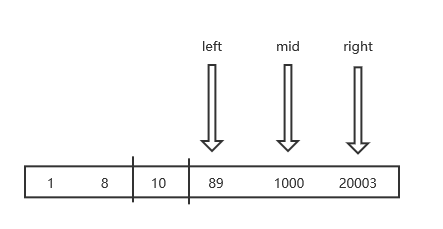
- 继续判断中间值与查找值,现在是等于,即找到了
Java实现二分查找
按照上面的步骤:
public class BinarySearch {
public static void main(String[] args) {
int[] arr = {1,8,10,89,1000,20003};
int index = binarySearch(arr,0,arr.length - 1,1000);
System.out.println("index = "+ index);
}
/**
* @param arr 要查找的数组
* @param left 左指针:指向查找的数组最左边
* @param right 右指针:指向查找的数组的最右边
* @param findVal 要查找的值
* @return 找到就返回下标,否则返回-1
*/
public static int binarySearch(int[] arr,int left,int right,int findVal){
num++;
//当left > right 时,递归了整个数组,没有找到
if (left > right){
return -1;
}
//中间指针
int mid = (left + right) / 2;
int midVal = arr[mid];
//如果找的值大于中间值,向右递归
if (findVal > midVal){
return binarySearch(arr,mid + 1,right,findVal);
}
//小于,向左递归
else if (findVal < midVal){
return binarySearch(arr,left,mid - 1,findVal);
}
else {
return mid;
}
}
}
得到结果:
但实际上还有点可以优化,当有多个相同的数时,被查找只能得到一个数
如:1,8,10,89,1000,1000,1000,20003,查找到第5个数10000就结束了,现在想返回所有数的集合
思路:当查找到要求的数时,先向左右查找,看是否存在相等的数,直到到达数组边界、找到不相等的数为止
public static List binarySearchList(int[] arr, int left, int right, int findVal){
//当left > right 时,递归了整个数组,没有找到
if (left > right){
return new ArrayList();
}
//中间指针
int mid = (left + right) / 2;
int midVal = arr[mid];
//如果找的值大于中间值,向右递归
if (findVal > midVal){
return binarySearchList(arr,mid + 1,right,findVal);
}
//小于,向左递归
else if (findVal < midVal){
return binarySearchList(arr,left,mid - 1,findVal);
}
else {
List<Integer> list = new ArrayList<>();
//当找到值arr[mid]时,判断左右两边是否有相同的值
//mid左
int temp = mid - 1;
while (true){
//当temp为最左边或者arr[temp] 不是要找的值
if (temp < 0 || arr[temp] != findVal){
break;
}
list.add(temp);
temp --;
}
//加入mid
list.add(mid);
//mid右
temp = mid + 1;
while (true){
//当temp为最左边或者arr[temp] 不是要找的值
if (temp > arr.length - 1 || arr[temp] != findVal){
break;
}
list.add(temp);
temp++;
}
return list;
}
}
查询:
public static void main(String[] args) {
int[] arr = {1,8,10,89,1000,1000,1000,20003};
List list = binarySearchList(arr,0,arr.length -1,1000);
System.out.println("list = "+ list);
}
非递归二分查找
前面使用递归实现了二分查找,这里用非递归法(循环)
/**
*
* @param arr 查找数组
* @param targert 待查找的数
* @return 返回对应下标,-1表示没找到
*/
public static int binarySearch(int[] arr,int targert){
int left = 0;
int right = arr.length -1;
while (left <= right){
int mid = (left + right) / 2;
if (arr[mid] == targert){
return mid;
}
//待查找的数在数组左边
else if (arr[mid] > targert){
//右指针移动到中点
right = mid -1;
}
//待查找的数在数组右边
else {
//左指针移动
left = mid + 1;
}
}
return -1;
}
测试:
public static void main(String[] args) {
int[] arr = {1,8,10,89,1000,20003};
int index = binarySearch(arr,1);
System.out.println("查找的数下标为 :"+index);
}
插值查找
插值查找算法的概念
当一个数组很长,且要查找的数在比较前或者比较后的位置,就需要多次二分,如果我们知道该值大概在什么位置就不需要查询多次,类似与字典查找时可以根据索引找到索引a开头的单词
二分查找仅是简单的按照数组的大小进行划分,插值查找是根据查找关键字与查找表中最大最小记录关键字比较后的查找方法
将二分查找的mid改为
mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left])
明显,插值查找也需要数组是有序的
例如:一个大小为100的数组,值对应为1~100
现需要查找1
- 当使用二分查找,mid分别为49,24,11,5,2,0
- 当使用插值查找,mid为0,直接查询到了
mid= 0 + (99-0)*(1-1)/(100-0)=0
Java实现插值查找
插值查找除了mid计算不同,其他都与二分查找相同
package com.company.search;
/**
* 插值查找算法
*/
public class InsertValSearch {
public static void main(String[] args) {
int[] arr = new int[100];
for (int i = 0;i < 100;i++){
arr[i] = i+1;
}
int i = insertValSearch(arr, 0, arr.length - 1, 1);
System.out.println("index = "+i);
}
//插值查找算法
/**
* @param arr 数组
* @param left 左边索引
* @param right 右边索引
* @param findVal 查找值
* @return 找到就返回对应的下标,否则-1
*/
public static int insertValSearch(int[] arr,int left,int right,int findVal){
//退出
if (left > right || findVal < arr[0] || findVal > arr[arr.length-1]){
return -1;
}
//求出mid
int mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);
int midValue = arr[mid];
//如果大于中间值,向右递归
if (findVal > midValue){
return insertValSearch(arr,mid + 1,right,findVal);
}
//如果小于中间值,向左递归
else if (findVal < midValue){
return insertValSearch(arr,left,mid - 1,findVal);
}
else {
return mid;
}
}
}
斐波拉契查找
斐波拉契查找算法的概念
斐波拉契查找算法与黄金比例、斐波拉契数列有关
斐波拉契数列:f(n) = f(n - 1) + f(n - 2),最开始两个数为1的数列,叫斐波拉契数列
10位斐波拉契数列:[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
黄金分割:是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值约为1:0.618或1.618:1,0.618被公认为最具有审美意义的比例数字
斐波拉契数列中,两个相邻的数,小值除大值就会靠近黄金比例,如2/3=0.667,3/5=0.6 … 34/55=0.6181
斐波拉契查找:
-
斐波拉契查找和前两种相似,也是改变mid值,mid位于黄金分割点附近
mid = low + f(k-1) - 1 -
就是根据数组的大小选择斐波拉契数列(如果数组大小不等于数列的值,填充值到大小等于最近的数列值),将数组分割成两个数组,例如数组大小为10,就将原数组填充值为大小13的数组,根据数列划分为5,8大小的数组
-
斐波那契查找也是二分查找的一种提升算法,通过运用黄金比例的概念在数列中选择查找点进行查找,提高查找效率。同样地,斐波那契查找也属于一种有序查找算法
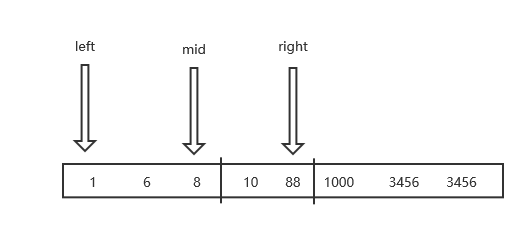
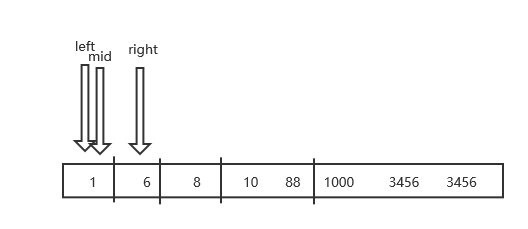
例如:数组1,6,8,10,88,1000,3456,查找1
- 数组大小为7,在最后填充一个值
1,6,8,10,88,1000,3456,3456,数组大小为8,根据数列划分为两个数组:1,6,8,10,88和1000,3456,3456,这个时候k=5
mid = low + f(k-1) - 1 = 0 + f(4) - 1 = 4,arr[mid]=88
- 按照二分查找,判断arr[mid]与查找的值的大小,小于即继续向左查找,
1,6,8,10,88划分为1,6,8和10,88
Java实现斐波拉契查找算法
首先,需要算出斐波拉契数列,然后根据斐波拉契数列划分数组,查找值
package com.company.search;
import java.util.ArrayList;
import java.util.Arrays;
/**
* @author zfk
* 斐波那契查找算法
*/
public class FibonacciSearch {
//斐波拉契数列大小
private static int maxSize = 20;
//查找次数
static int num = 0;
public static void main(String[] args) {
int[] arr = {1,6,8,10,88,1000,3456};
System.out.println("index = "+fibSearch(arr,1));
System.out.println("查找次数:"+num);
}
/**
* @return 返回斐波拉契数列
*/
public static int[] fib(){
int[] f = new int[maxSize];
f[0] = 1;
f[1] = 1;
for (int i = 2;i < maxSize;i++){
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
/**
* @param arr 查找的数组
* @param key 查找的数
* @return 返回对应的下标,没有为-1
*/
//斐波拉契查找算法
public static int fibSearch(int[] arr,int key){
int low = 0;
int high = arr.length - 1;
//斐波拉契要分割的数值的下标
int k = 0;
//存放mid值
int mid = 0;
//获取斐波拉契数列
int[] f = fib();
//获取斐波拉契数列的分割点的下标
while (high > f[k] - 1){
k++;
}
//因为f[k]可能大于数组arr,需要构造一个新的数组
int[] temp = Arrays.copyOf(arr,f[k]);
//补齐temp,可以使用arr数组最后的数填充temp后面的0
for (int i = high + 1;i < temp.length;i++){
temp[i] = arr[high];
}
//找到key
while (low <= high){
num++;
mid = low + f[k-1] -1;
//继续向数组的左边查找
if (key < temp[mid]){
high = mid - 1;
//下一步斐波拉契数列为f[k-1-1]
k--;
}
//向数组的右边找
else if (key > temp[mid]){
low = mid + 1;
//f[k] = f[k-1] + f[k-2] ,后面为f[k-2]相差的位置为2
k -= 2;
}
else {
//找到,返回小的下标
return Math.min(mid,high);
}
}
//没有找到
return -1;
}
}
总结
这里介绍了4中查找算法
当数组无序时,只能用顺序查找从头开始找
当数组有序时,可以选择这3种有序查找:
- 二分查找:根据mid值均分数组,比较arr[mid]与查找值,不相等就继续递归划分查找
- 插值查找:在二分查找的基础上优化,
mid=low+(right-left)*(findVal-arr[left])/(arr[right]-arr[left]),这样划分数组时可以根据查找值与数组最大最小值的比例有效划分数组 - 斐波拉契查找:与上面两种相似,根据斐波拉契数列划分数组
在不同的情况下,二分查找、插值查找、斐波拉契查找效率不同
有7种查找算法,树表查找,分块查找,哈希查找后续实现