Python监督学习（一）

Python监督学习

简介

如果你熟悉机器学习的基础知识，那么肯定知道什么是监督学习。监督学习是指在有标记的样本（labeled samples）上建立机器学习的模型。例如，如果用尺寸、位置等不同参数建立一套模型来评估一栋房子的价格，那么首先需要创建一个数据库，然后为参数打上标记。我们需要告诉算法，什么样的参数（尺寸、位置）对应什么样的价格。有了这些带标记的数据，算法就可以学会如何根据输入的参数计算房价了。

无监督学习与刚才说的恰好相反，它面对的是没有标记的数据。假设需要把一些数据分成不同的组别，但是对分组的条件毫不知情，于是，无监督学习算法就会以最合理的方式将数据集分成确定数量的组别。

建立各种模型时，将使用许多Python程序包，像NumPy、SciPy、scikit-learn、matplotlib等。如果你使用Windows系统，推荐安装兼容SciPy关联程序包的Python发行版，网址为http://www.scipy.org/install.html，这些Python发行版里已经集成了常用的程序包。如果你使用Mac OS X或者Ubuntu系统，安装这些程序包就相当简单了。下面列出来程序包安装和使用文档的链接：

NumPy：http://docs.scipy.org/doc/numpy-1.10.1/user/install.html

SciPy：http://www.scipy.org/install.html

scikit-learn：http://scikit-learn.org/stable/install.html

matplotlib：http://matplotlib.org/1.4.2/users/installing.html

现在，请确保你的计算机已经安装了所有程序包。

数据预处理技术

在真实世界中，经常需要处理大量的原始数据，这些原始数据是机器学习算法无法理解的。为了让机器学习算法理解原始数据，需要对数据进行预处理。

准备工作

来看看Python是如何对数据进行预处理的。首先，用你最喜欢的文本编辑器打开一个扩展名为.py的文件，例如preprocessor.py。然后在文件里加入下面两行代码：

import numpy as np
from sklearn import preprocessing

我们只是加入了两个必要的程序包。接下来创建一些样本数据。向文件中添加下面这行代码：

data = np.array([[3,-1.5,2,-5.4], [0,4,-0.3,2.1], [1,3.3,
-1.9, -4.3]])

现在就可以对数据进行预处理了。

1.2.2　详细步骤
数据可以通过许多技术进行预处理，接下来将介绍一些最常用的预处理技术。

均值移除（Mean removal）

通常我们会把每个特征的平均值移除，以保证特征均值为0（即标准化处理）。这样做可以消除特征彼此间的偏差（bias）。将下面几行代码加入之前打开的Python文件中：

data_standardized = preprocessing.scale(data)
print "\nMean =", data_standardized.mean(axis=0)
print "Std deviation =", data_standardized.std(axis=0)

现在来运行代码。打开命令行工具，然后输入以下命令：

$ python preprocessor.py

命令行工具中将显示以下结果：

Mean = [  5.55111512e-17  -1.11022302e-16  -7.40148683e-17  -7.40148683e-17]
Std deviation = [ 1.  1.  1.  1.]

你会发现特征均值几乎是0，而且标准差为1。

范围缩放（Scaling）

数据点中每个特征的数值范围可能变化很大，因此，有时将特征的数值范围缩放到合理的大小是非常重要的。在Python文件中加入下面几行代码，然后运行程序：

data_scaler = preprocessing.MinMaxScaler(feature_range=(0, 1))
data_scaled = data_scaler.fit_transform(data)
print "\nMin max scaled data =", data_scaled

范围缩放之后，所有数据点的特征数值都位于指定的数值范围内。输出结果如下所示：

Min max scaled data:
[[ 1.            0.            1.            0.        ]
 [ 0.            1.            0.41025641    1.        ]
 [ 0.33333333    0.87272727    0.            0.14666667]]

归一化（Normalization）

数据归一化用于需要对特征向量的值进行调整时，以保证每个特征向量的值都缩放到相同的数值范围。机器学习中最常用的归一化形式就是将特征向量调整为L1范数，使特征向量的数值之和为1。增加下面两行代码到前面的Python文件中：

data_normalized = preprocessing.normalize(data, norm='l1')
print "\nL1 normalized data =", data_normalized

执行Python文件，就可以看到下面的结果：

L1    normalized    data:
[[    0.25210084    -0.12605042    0.16806723    -0.45378151]
 [    0.             0.625        -0.046875       0.328125  ]
 [    0.0952381      0.31428571   -0.18095238    -0.40952381]]

这个方法经常用于确保数据点没有因为特征的基本性质而产生较大差异，即确保数据处于同一数量级，提高不同特征数据的可比性。

二值化（Binarization）

二值化用于将数值特征向量转换为布尔类型向量。增加下面两行代码到前面的Python文件中：

data_binarized = preprocessing.Binarizer(threshold=1.4).transform(data)
print "\nBinarized data =", data_binarized

再次执行Python文件，就可以看到下面的结果：

Binarized data:
[[    1.    0.    1.    0.]
 [    0.    1.    0.    1.]
 [    0.    1.    0.    0.]]

如果事先已经对数据有了一定的了解，就会发现使用这个技术的好处了。

独热编码

通常，需要处理的数值都是稀疏地、散乱地分布在空间中，然而，我们并不需要存储这些大数值，这时就需要使用独热编码（One-Hot Encoding）。可以把独热编码看作是一种收紧（tighten）特征向量的工具。它把特征向量的每个特征与特征的非重复总数相对应，通过one-of-k 的形式对每个值进行编码。特征向量的每个特征值都按照这种方式编码，这样可以更加有效地表示空间。例如，我们需要处理4维向量空间，当给一个特性向量的第n 个特征进行编码时，编码器会遍历每个特征向量的第n 个特征，然后进行非重复计数。如果非重复计数的值是K，那么就把这个特征转换为只有一个值是1其他值都是0的K 维向量。增加下面几行代码到前面的Python文件中：

encoder = preprocessing.OneHotEncoder()
encoder.fit([[0, 2, 1, 12], [1, 3, 5, 3], [2, 3, 2, 12], [1, 2, 4, 3]])
encoded_vector = encoder.transform([[2, 3, 5, 3]]).toarray()
print "\nEncoded vector =", encoded_vector

结果如下所示：

Encoded vector:
[[ 0.  0.  1.  0.  1.  0.  0.  0.  1.  1.  0.]]

在上面的示例中，观察一下每个特征向量的第三个特征，分别是1、5、2、4这4个不重复的值，也就是说独热编码向量的长度是4。如果你需要对5进行编码，那么向量就是[0, 1, 0, 0]。向量中只有一个值是1。第二个元素是1，对应的值是5。

标记编码方法

在监督学习中，经常需要处理各种各样的标记。这些标记可能是数字，也可能是单词。如果标记是数字，那么算法可以直接使用它们，但是，许多情况下，标记都需要以人们可理解的形式存在，因此，人们通常会用单词标记训练数据集。标记编码就是要把单词标记转换成数值形式，让算法懂得如何操作标记。接下来看看如何标记编码。

详细步骤

(1) 新建一个Python文件，然后导入preprocessing程序包：

from sklearn import preprocessing

(2) 这个程序包包含许多数据预处理需要的函数。定义一个标记编码器（label encoder），代码如下所示：

label_encoder = preprocessing.LabelEncoder()

(3) label_encoder对象知道如何理解单词标记。接下来创建一些标记：

input_classes = ['audi', 'ford', 'audi', 'toyota', 'ford', 'bmw']

(4) 现在就可以为这些标记编码了：

label_encoder.fit(input_classes)
print "\nClass mapping:"
for i, item in enumerate(label_encoder.classes_):
    print item, '-->', i

(5) 运行代码，命令行工具中显示下面的结果：

Class mapping:
audi --> 0
bmw --> 1
ford --> 2
toyota --> 3

(6) 就像前面结果显示的那样，单词被转换成从0开始的索引值。现在，如果你遇到一组标记，就可以非常轻松地转换它们了，如下所示：

labels = ['toyota', 'ford', 'audi']
encoded_labels = label_encoder.transform(labels)
print "\nLabels =", labels
print "Encoded labels =", list(encoded_labels)

命令行工具中将显示下面的结果：

Labels = ['toyota', 'ford', 'audi']
Encoded labels = [3, 2, 0]

(7) 这种方式比纯手工进行单词与数字的编码要简单许多。还可以通过数字反转回单词的功能检查结果的正确性：

encoded_labels = [2, 1, 0, 3, 1]
decoded_labels = label_encoder.inverse_transform(encoded_labels)
print "\nEncoded labels =", encoded_labels
print "Decoded labels =", list(decoded_labels)

结果如下所示：

Encoded labels = [2, 1, 0, 3, 1]
Decoded labels = ['ford', 'bmw', 'audi', 'toyota', 'bmw']

可以看到，映射结果是完全正确的。

1.4　创建线性回归器

回归是估计输入数据与连续值输出数据之间关系的过程。数据通常是实数形式的，我们的目标是估计满足输入到输出映射关系的基本函数。让我们从一个简单的示例开始。考虑下面的输入与输出映射关系：

1 → 2

3 → 6

4.3 → 8.6

7.1 → 14.2

如果要你估计输入与输出的关联关系，你可以通过模式匹配轻松地找到结果。我们发现输出结果一直是输入数据的两倍，因此输入与输出的转换公式就是这样：

f(x) = 2x

这是体现输入值与输出值关联关系的一个简单函数。但是，在真实世界中通常都不会这么简单，输入与输出的映射关系函数并不是一眼就可以看出来的。

1.4.1　准备工作
线性回归用输入变量的线性组合来估计基本函数。前面的示例就是一种单输入单输出变量的线性回归。

现在考虑如图1-1所示的情况。

线性回归的目标是提取输入变量与输出变量的关联线性模型，这就要求实际输出与线性方程预测的输出的残差平方和（sum of squares of differences）最小化。这种方法被称为普通最小二乘法（Ordinary Least Squares，OLS）。

你可能觉得用一条曲线对这些点进行拟合效果会更好，但是线性回归不允许这样做。线性回归的主要优点就是方程简单。如果你想用非线性回归，可能会得到更准确的模型，但是拟合速度会慢很多。线性回归模型就像前面那张图里显示的，用一条直线近似数据点的趋势。接下来看看如何用Python建立线性回归模型。

详细步骤

假设你已经创建了数据文件data_singlevar.txt，文件里用逗号分隔符分割字段，第一个字段是输入值，第二个字段是与逗号前面的输入值相对应的输出值。你可以用这个文件作为输入参数。

(1) 创建一个Python文件regressor.py，然后在里面增加下面几行代码：

import sys
import numpy as np
filename = sys.argv[1]
X = []
y = []
with open(filename, 'r') as f:
    for line in f.readlines():
        xt, yt = [float(i) for i in line.split(',')]
        X.append(xt)
        y.append(yt)

把输入数据加载到变量X和y，其中X是数据，y是标记。在代码的for循环体中，我们解析每行数据，用逗号分割字段。然后，把字段转化为浮点数，并分别保存到变量X和y中。

(2) 建立机器学习模型时，需要用一种方法来验证模型，检查模型是否达到一定的满意度（satisfactory level）。为了实现这个方法，把数据分成两组：训练数据集（training dataset）与测试数据集（testing dataset）。训练数据集用来建立模型，测试数据集用来验证模型对未知数据的学习效果。因此，先把数据分成训练数据集与测试数据集：

num_training = int(0.8 * len(X))
num_test = len(X) - num_training

# 训练数据
X_train = np.array(X[:num_training]).reshape((num_training,1))
y_train = np.array(y[:num_training])

# 测试数据
X_test = np.array(X[num_training:]).reshape((num_test,1))
y_test = np.array(y[num_training:])

这里用80%的数据作为训练数据集，其余20%的数据作为测试数据集。

(3) 现在已经准备好训练模型。接下来创建一个回归器对象，代码如下所示：

from sklearn import linear_model

# 创建线性回归对象
linear_regressor = linear_model.LinearRegression()

# 用训练数据集训练模型
linear_regressor.fit(X_train, y_train)

(4) 我们利用训练数据集训练了线性回归器。向fit方法提供输入数据即可训练模型。用下面的代码看看它如何拟合：

import matplotlib.pyplot as plt

y_train_pred = linear_regressor.predict(X_train)
plt.figure()
plt.scatter(X_train, y_train, color='green')
plt.plot(X_train, y_train_pred, color='black', linewidth=4)
plt.title('Training data')
plt.show()

(5) 在命令行工具中执行如下命令：

$ python regressor.py data_singlevar.txt

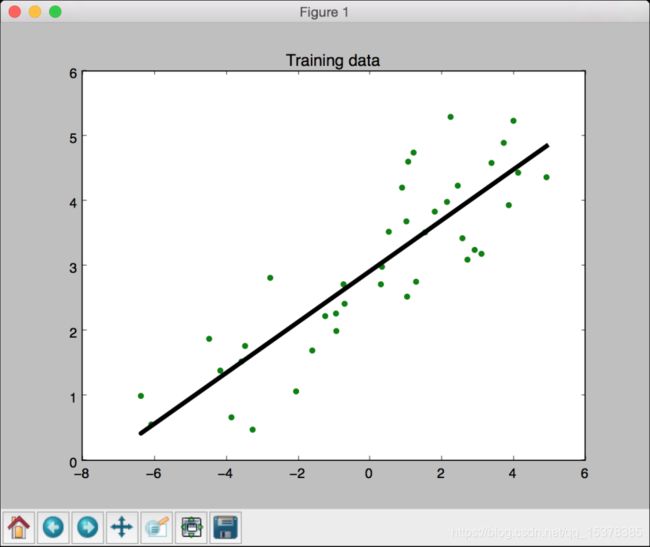
就会看到如图1-2所示的线性回归。

(6) 在前面的代码中，我们用训练的模型预测了训练数据的输出结果，但这并不能说明模型对未知的数据也适用，因为我们只是在训练数据上运行模型。这只能体现模型对训练数据的拟合效果。从图1-2中可以看到，模型训练的效果很好。

(7) 接下来用模型对测试数据集进行预测，然后画出来看看，代码如下所示：

y_test_pred = linear_regressor.predict(X_test)

plt.scatter(X_test, y_test, color='green')
plt.plot(X_test, y_test_pred, color='black', linewidth=4)
plt.title('Test data')
plt.show()

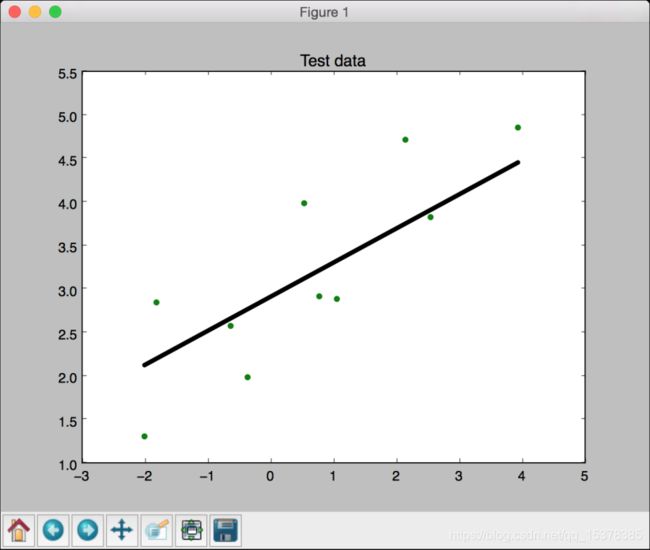
运行代码，可以看到如图1-3所示的线性回归。

推荐参考学习书籍：Python机器学习经典实例