数据结构 - 顺序表基本操作
目录
前言：
接口实现
顺序表基本操作
顺序表初始化（SeqListInit）
检查空间进行增容（SeqListCheckCapacity）
顺序表打印（SeqListPrint）
销毁（SeqListDestroy）
1、尾插（SeqListPushBack）
2、尾删（SeqListPopBack）
3、头插（SeqListPushFront）
4、头删（SeqListPopFront）
5、查找位置（SeqListFind）
6、在指定的下标位置插入（SeqListInsert）
7、删除指定位置的数据（SeqListErase）
代码封装优化
完整代码：
SeqList.h：头文件以及函数申明
SeqList.c：接口实现
OJ练习：
前言：
线性表
线性表 （ linear list ） 是 n 个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结 构，常见的线性表：顺序表、链表、栈、队列、字符串...
线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物 理上存储时，通常以数组和链式结构的形式存储。
顺序表
顺序表是用一段 物理地址连续 的存储单元依次存储数据元素的线性结构，一般情况下采用数组存储。在数组
上完成数据的增删查改。
顺序表一般可以分为：
1. 静态顺序表：使用定长数组存储元素 。
#define N 7
typedef int SLDataType
typedef struct SeqList {
SLDataType array[N]; //定长数组
size_t size; //有效数据的个数
} SeqList;
2. 动态顺序表：使用动态开辟的数组存储。
typedef int SLDataType
typedef struct SeqList {
SLDataType* array; //指向动态开辟的数组
size_t size; //有效数据的个数
size_t capacity; //容量空间的大小
} SeqList;
接口实现
静态顺序表只适用于确定知道需要存多少数据的场景。静态顺序表的定长数组导致 N 定大了，空间开多了浪 费，开少了不够用。所以现实中基本都是使用动态顺序表，根据需要动态的分配空间大小，所以下面我们实 现动态顺序表。
为了方便后续修改数据类型，我们可以使用 typedef 定义一个新的数据类型，这里我们把它取名为 SLDataType为了让定义的结构体使用时更方便，我们同样可以使用 typedef 将其定义为 SeqList（此时 SeqList = struct SeqList，后续在使用时可以更加方便）。
typedef int SLDataType;
// 顺序表的动态存储
typedef struct SeqList
{
SLDataType* array; // 指向动态开辟的数组
size_t size ; // 有效数据个数
size_t capicity ; // 容量空间的大小
}SeqList;顺序表的所以基本操作：
// 基本增删查改接口
// 顺序表初始化
void SeqListInit(SeqList* psl, size_t capacity);
// 检查空间，如果满了，进行增容
void SeqListCheckCapacity(SeqList* psl);
// 顺序表尾插
void SeqListPushBack(SeqList* psl, SLDataType x);
// 顺序表尾删
void SeqListPopBack(SeqList* psl);
// 顺序表头插
void SeqListPushFront(SeqList* psl, SLDataType x);
// 顺序表头删
void SeqListPopFront(SeqList* psl);
// 顺序表查找
int SeqListFind(SeqList* psl, SLDataType x);
// 顺序表在pos位置插入x
void SeqListInsert(SeqList* psl, size_t pos, SLDataType x);
// 顺序表删除pos位置的值
void SeqListErase(SeqList* psl, size_t pos);
// 顺序表销毁
void SeqListDestory(SeqList* psl);
// 顺序表打印
void SeqListPrint(SeqList* psl);顺序表基本操作
前情提要：assert()函数
#include "assert.h" void assert( int expression );
assert 的作用是现计算表达式 expression ，如果其值为假（即为0）或者为NULL，那么将直接报错。（断言(assert)的用法 | 菜鸟教程 (runoob.com)）
下文中 assert(psl);用于防止错误并方便Debug，因为assert会精准的报出错误位置；
顺序表初始化（SeqListInit）
void SeqListInit(SeqList* psl)
{
assert(psl);
psl->a = NULL;
psl->size = 0; //有效数据个数
psl->capacity = 0; //数组实际能存数据的空间容量是多大
}检查空间进行增容（SeqListCheckCapacity）
size_t等价于unsigned int
void SeqListCheckCapacity(SeqList* psl)
{
assert(psl);
// 如果满了，我们要扩容
if (psl->size == psl->capacity)
{
size_t newCapacity = psl->capacity == 0 ? 4 : psl->capacity * 2;
SLDataType* tmp = realloc(psl->a, sizeof(SLDataType) * newCapacity);
if (tmp == NULL)
{
printf("realloc fail\n");//扩容失败，直接退出
exit(-1);
}
else
{
psl->a = tmp;
psl->capacity = newCapacity;
}
}
}- 这里巧妙地使用三目操作符：int new_capacity = psl->capacity == 0 ? 4 : psl->capacity*2 ， 如果 capacity 为 0 （第一次使用大小是0），就把4赋值给它；如果不为0，就把 capacity 的值翻一倍（x2）。
- 你想一次扩容多少就扩容多少，乘2只是一个比较折中的扩容容量方案。
顺序表打印（SeqListPrint）
void SeqListPrint(SeqList* psl)
{
assert(psl);
for (int i = 0; i < psl->size; ++i)
{
printf("%d ", psl->a[i]);
}
printf("\n");
}
因为是单纯的打印，所以只需要把顺序表传过去就行。
销毁（SeqListDestroy）
因为是动态开辟的，所以如果空间不用我们就需要销毁掉。如果不销毁会存在内存泄漏的风险，所以与之对应的我们写一个销毁的接口函数。
void SeqListDestroy(SeqList* psl)
{
assert(psl);
free(psl->a);
psl->a = NULL;
psl->capacity = psl->size = 0;
}1、尾插（SeqListPushBack）
void SeqListPushBack(SeqList* psl, SLDataType x)
{
assert(psl);
SeqListCheckCapacity(psl);//查看是否要扩容
psl->a[psl->size] = x;
psl->size++;
}
2、尾删（SeqListPopBack）
void SeqListPopBack(SeqList* psl)
{
assert(psl);
//psl->a[psl->size - 1] = 0;
if (psl->size > 0)
{
psl->size--;
}
}
对于尾删，其实只要让最后一个元素访问不到就行，即size--即可。
3、头插（SeqListPushFront）
void SeqListPushFront(SeqList* psl, SLDataType x)
{
assert(psl);
SeqListCheckCapacity(psl);
// 挪动数据，腾出头部空间
int end = psl->size - 1;
while (end >= 0)
{
psl->a[end + 1] = psl->a[end];
--end;
}
psl->a[0] = x;
psl->size++;
}
4、头删（SeqListPopFront）
void SeqListPopFront(SeqList* psl)
{
assert(psl);
// 挪动数据覆盖删除
if (psl->size > 0)
{
int begin = 1;
while (begin < psl->size)
{
psl->a[begin - 1] = psl->a[begin];
++begin;
}
--psl->size; //相当于让指针指向第二个元素
}
}
5、查找位置（SeqListFind）
int SeqListFind(SeqList* psl, SLDataType x)
{
assert(psl);
for (int i = 0; i < psl->size; ++i)
{
if (psl->a[i] == x)
{
return i;
}
}
return -1;
}6、在指定的下标位置插入（SeqListInsert）
void SeqListInsert(SeqList* psl, size_t pos, SLDataType x)
{
// 暴力检查
assert(psl);
// 温和检查
if (pos > psl->size)
{
printf("pos 越界：%d\n", pos);
return;
}
SeqListCheckCapacity(psl);
size_t end = psl->size;
while (end > pos)
{
psl->a[end] = psl->a[end - 1];
--end;
}
psl->a[pos] = x;
psl->size++;
}
7、删除指定位置的数据（SeqListErase）
void SeqListErase(SeqList* psl, size_t pos)
{
assert(psl);
assert(pos < psl->size);
size_t begin = pos + 1;
while (begin < psl->size)
{
psl->a[begin - 1] = psl->a[begin];
++begin;
}
psl->size--;
}
此时，我们发现代码有许多共同点；比如头插、尾插不就是SeqListInsert在下标为0和下标为size（）时插入吗？同理：头删、尾删也可以用SeqListErase代替
代码封装优化
void SeqListPushBack(SeqList* psl, SLDataType x)
{
assert(psl);
SeqListInsert(psl, psl->size, x);
}
void SeqListPopBack(SeqList* psl)
{
assert(psl);
SeqListErase(psl, psl->size - 1);
}
void SeqListPushFront(SeqList* psl, SLDataType x)
{
assert(psl);
SeqListInsert(psl, 0, x);
}
void SeqListPopFront(SeqList* psl)
{
assert(psl);
SeqListErase(psl, 0);
}完整代码：
SeqList.h：头文件以及函数申明
#pragma once//为了避免同一个头文件被包含多次我们可以使用 #pragma once
#include
#include
#include
// 要求：存储的数据从0开始，依次连续存储
// 静态的顺序表
// 问题：开小了，不够用。开大了，存在浪费。
//#define N 10000
//struct SeqList
//{
// int a[N];
// int size; // 记录存储了多少个数据
//};
typedef int SLDataType;
// 动态的顺序表
typedef struct SeqList
{
SLDataType* a;
int size; // 存储数据个数
int capacity; // 存储空间大小
}SL, SeqList;
void SeqListPrint(SeqList* psl);
//void SLInit(SeqList* psl);
void SeqListInit(SeqList* psl);
void SeqListDestroy(SeqList* psl);
void SeqListCheckCapacity(SeqList* psl);
// 时间复杂度是O(1)
void SeqListPushBack(SeqList* psl, SLDataType x);
void SeqListPopBack(SeqList* psl);
// 时间复杂度是O(N)
void SeqListPushFront(SeqList* psl, SLDataType x);
void SeqListPopFront(SeqList* psl);
// 在pos位置插入x
void SeqListInsert(SeqList* psl, size_t pos, SLDataType x);
// 删除pos位置的数据
void SeqListErase(SeqList* psl, size_t pos);
// 顺序表查找
int SeqListFind(SeqList* psl, SLDataType x);
SeqList.c：接口实现
#include "SeqList.h"
void SeqListPrint(SeqList* psl)
{
assert(psl);
for (int i = 0; i < psl->size; ++i)
{
printf("%d ", psl->a[i]);
}
printf("\n");
}
void SeqListInit(SeqList* psl)
{
assert(psl);
psl->a = NULL;
psl->size = 0;
psl->capacity = 0;
}
void SeqListDestroy(SeqList* psl)
{
assert(psl);
free(psl->a);
psl->a = NULL;
psl->capacity = psl->size = 0;
}
void SeqListCheckCapacity(SeqList* psl)
{
assert(psl);
// 如果满了，我们要扩容
if (psl->size == psl->capacity)
{
size_t newCapacity = psl->capacity == 0 ? 4 : psl->capacity * 2;
SLDataType* tmp = realloc(psl->a, sizeof(SLDataType) * newCapacity);
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
else
{
psl->a = tmp;
psl->capacity = newCapacity;
}
}
}
void SeqListPushBack(SeqList* psl, SLDataType x)
{
assert(psl);
SeqListInsert(psl, psl->size, x);
}
void SeqListPopBack(SeqList* psl)
{
assert(psl);
SeqListErase(psl, psl->size - 1);
}
void SeqListPushFront(SeqList* psl, SLDataType x)
{
assert(psl);
SeqListInsert(psl, 0, x);
}
void SeqListPopFront(SeqList* psl)
{
assert(psl);
SeqListErase(psl, 0);
}
// 在pos位置插入x
void SeqListInsert(SeqList* psl, size_t pos, SLDataType x)
{
// 暴力检查
assert(psl);
// 温和检查
if (pos > psl->size)
{
printf("pos 越界：%d\n", pos);
return;
//exit(-1);
}
// 暴力检查
//assert(pos <= psl->size);
SeqListCheckCapacity(psl);
size_t end = psl->size;
while (end > pos)
{
psl->a[end] = psl->a[end - 1];
--end;
}
psl->a[pos] = x;
psl->size++;
}
// 删除pos位置的数据
void SeqListErase(SeqList* psl, size_t pos)
{
assert(psl);
assert(pos < psl->size);
size_t begin = pos + 1;
while (begin < psl->size)
{
psl->a[begin - 1] = psl->a[begin];
++begin;
}
psl->size--;
}
int SeqListFind(SeqList* psl, SLDataType x)
{
assert(psl);
for (int i = 0; i < psl->size; ++i)
{
if (psl->a[i] == x)
{
return i;
}
}
return -1;
}笔记篇：参考资料->比特科技
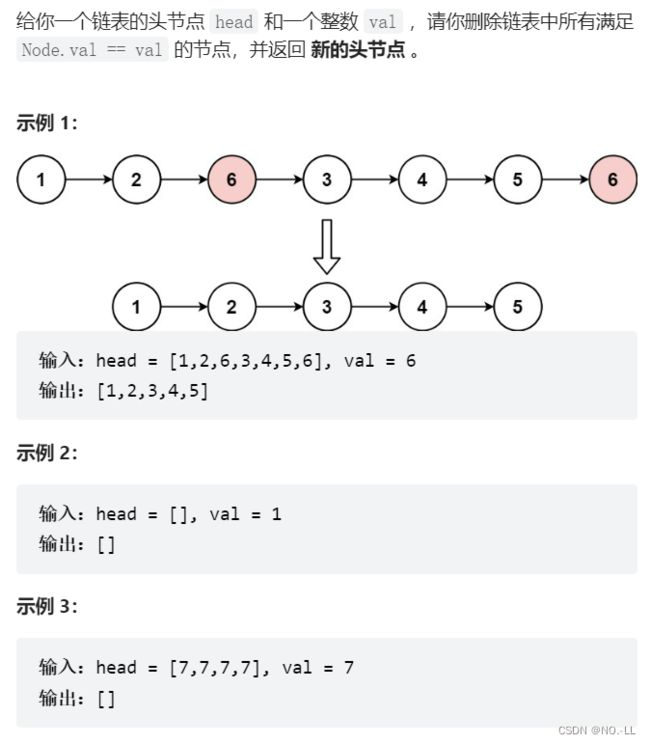
OJ练习：
链表的结构图：
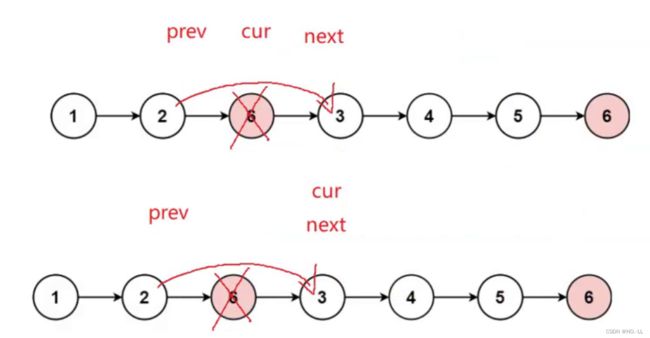
203. 移除链表元素
思路：
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* removeElements(struct ListNode* head, int val){
struct ListNode*prve=NULL;
struct ListNode*cur=head;
while(cur){ //遍历整个数组
if(cur->val!=val){ //如果不是，则共同前进一步
prve=cur;
cur=cur->next;
}
else{ //如果是，则如图所示
struct ListNode*next=cur->next;
if(prve==NULL){ //头删情况，因为头删时没有prve->next
free(cur);
head=next;
cur=head;
}
else{
free(cur);
prve->next=next;
cur=next;
}
}
}
return head;
}206. 反转链表
思路：直接把链表的指向反转即可
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
struct ListNode*newHead=NULL;
struct ListNode*cur=head;
while(cur){
struct ListNode*next=cur->next;
cur->next=newHead; //将“箭头”反转
newHead=cur;
cur=next;
}
return newHead;
}
};/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head==NULL)
return NULL;
struct ListNode*n1,*n2,*n3;
n1=NULL;
n2=head;
n3=n2->next;
while(n2){
n2->next=n1;
n1=n2;
n2=n3;
if(n3) //作图可知，最后一个n3=NULL，无n3->next
n3=n3->next;
}
return n1;
}
};C++写法
方法一：迭代
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* p=nullptr;
ListNode* curr=head;
while(curr)
{
ListNode* next=curr->next;
curr->next=p;
p=curr;
curr=next;
}
return p;
}
};方法二：递归
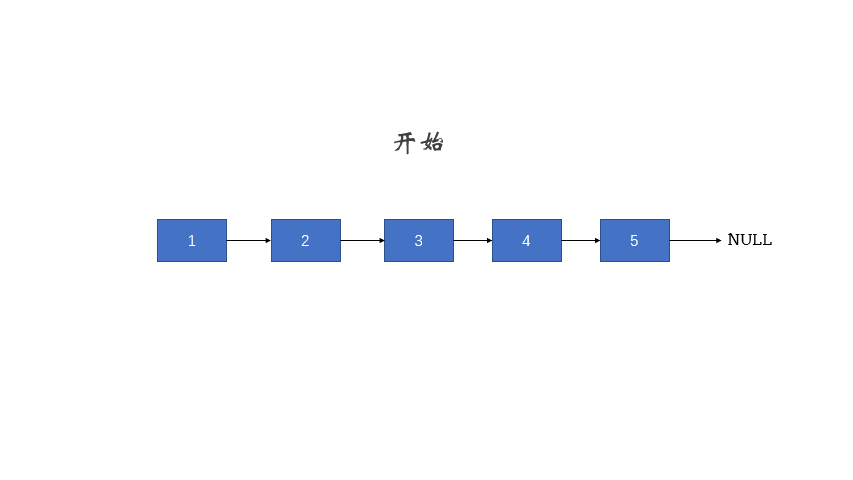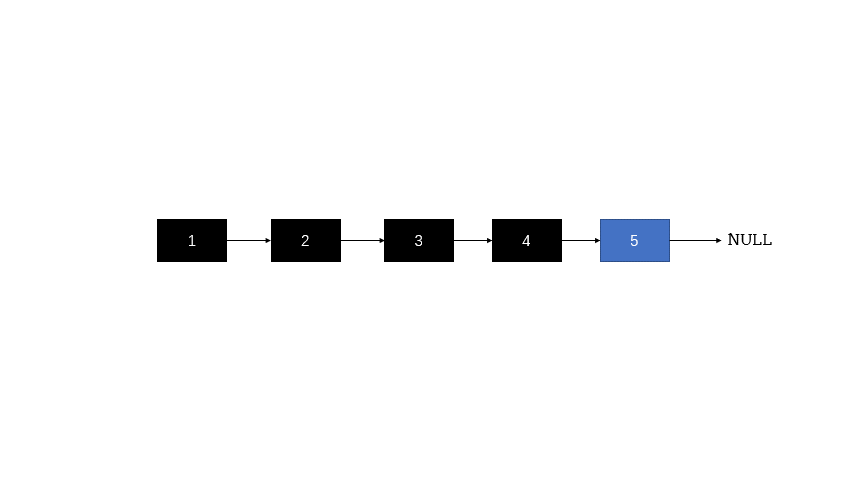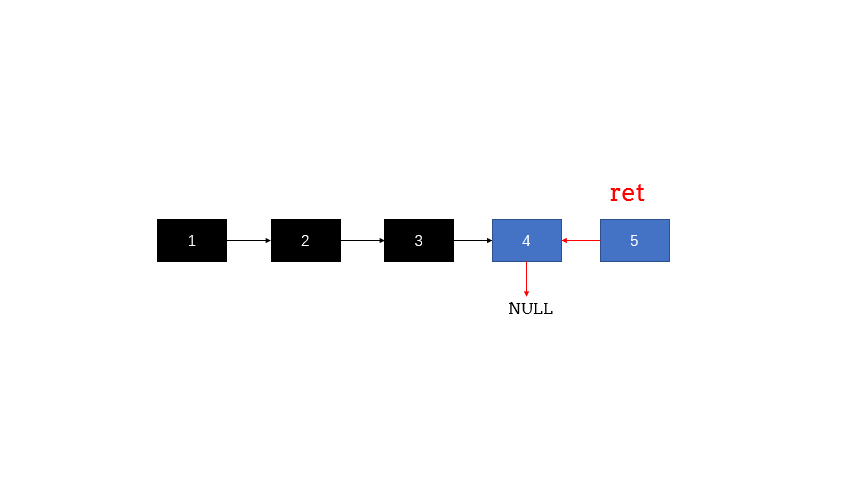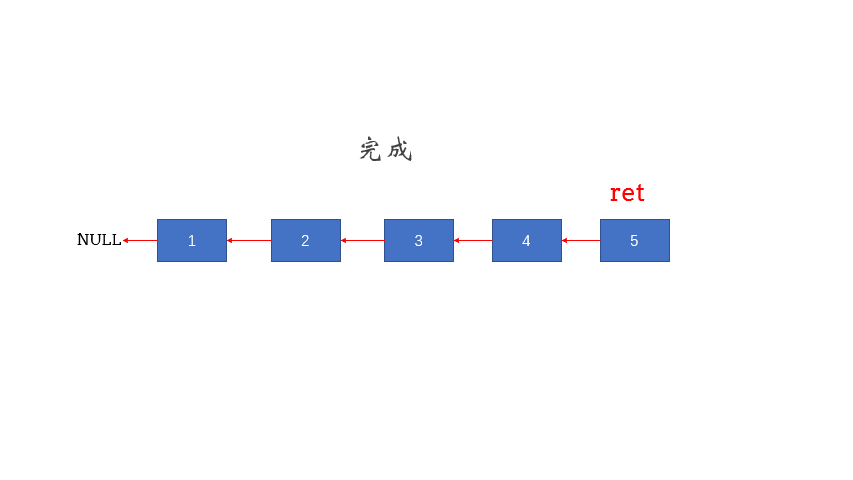
- 使用递归函数，一直递归到链表的最后一个结点，该结点就是反转后的头结点，记作 retret .
- 此后，每次函数在返回的过程中，让当前结点的下一个结点的 nextnext 指针指向当前节点。
- 同时让当前结点的 nextnext 指针指向 NULLNULL ，从而实现从链表尾部开始的局部反转
- 当递归函数全部出栈后，链表反转完成。
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(!head||!head->next)
return head;
ListNode* ret=reverseList(head->next);
head->next->next=head;
head->next=NULL;
return ret;
}
};26. 删除有序数组中的重复项 - 力扣（LeetCode）
经典快慢指针！！
class Solution {
public:
int removeDuplicates(vector& nums) {
int n=nums.size();
int slow=1,fast=1;
while(fast