C++进阶——AVL树
文章目录
-
-
-
- C++进阶——AVL树
- AVL树的概念
- AVL树的实现
-
- AVL树节点的定义
- AVL树的四个默认成员函数
-
- 构造函数
- 拷贝构造
- 析构函数
- 赋值运算符重载
- AVL树的插入
-
- 插入的步骤
- 平衡因子的调节
- 旋转处理(父节点的平衡因子违法平衡树的性质)
- 代码实现
- []运算符的重载
- AVL树的查找
- AVL树的打印
- 验证是否为AVL树
- AVL树代码实现
-
-
C++进阶——AVL树
AVL树的概念
在前面的文章中我们学习了二叉搜索树,但是二叉搜索树虽然可以缩短查找的效率,但是 如果数据有序或者接近有序的情况下二叉搜索树会退化成单支树,查找元素相当于在顺序表中搜索元素,效率低下。
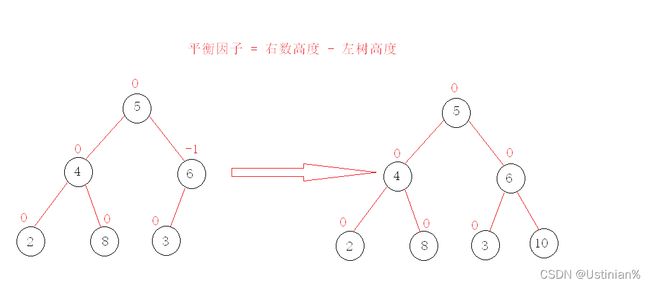
因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整), 即可降低树的高度,从而减少平均搜索长度。
一棵AVL树具有以下性质:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
如果一棵二叉搜索树的高度是平衡的,那么它就是AVL树。如果该二叉搜索树中有n个节点,其搜索时间复杂度可以达到O(log2N)
AVL树的实现
AVL树节点的定义
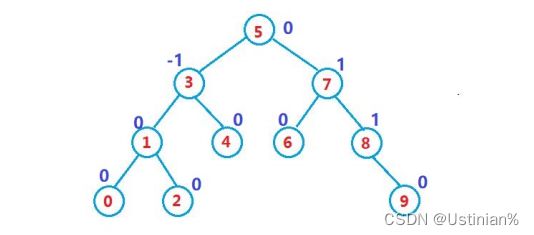
我们这里的节点采用了三叉链的形式,节点中存放了该节点的平衡因子以及该元素的数据。
template<class K, class V>
struct AVLTreeNode
{
//三叉链
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
int _bf;//平衡因子
pair<K, V> _kv;
//构造函数
AVLTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _bf(0)
, _kv(kv)
{}
};
AVL树的四个默认成员函数
构造函数
//构造函数
AVLTree()
:_root(nullptr)
{}
拷贝构造
这里的拷贝构造和二叉搜索树的拷贝构造的实现类似,实现一个Copy函数然后去调用Copy函数进行拷贝构造
Node* _Copy(Node* root)
{
if (root == nullptr)
{
return nullptr;
}
Node* CopyNode = new Node(root->_kv);
//将当前节点的平衡因子赋给CopyNode
CopyNode->_bf = root->_bf;
//更新CopyNode的父节点
Node* Parent = nullptr;
if (root->_parent)
{
Parent = new Node(root->_parent->_kv);
}
CopyNode->_parent = Parent;
//递归调用
CopyNode->_left = _Copy(root->_left);
CopyNode->_right = _Copy(root->_right);
return CopyNode;
}
//拷贝构造
AVLTree(const AVLTree<K, V>& temp)
{
_root = _Copy(temp._root);
}
析构函数
我们这里析构函数需要将从根节点到叶子节点的每个节点都释放掉,否则就会有内存泄漏的风险。因此我们这里通过实现一个Destory函数然后调用Destory函数来帮助我们去析构
void _Destory(Node* root)
{
//如果遇到空结点就返回
if (root == nullptr)
{
return;
}
//采用后续遍历的方式删除结点
_Destory(root->_left);
_Destory(root->_right);
delete root;
}
//析构函数
~AVLTree()
{
_Destory(_root);
_root = nullptr;
}
赋值运算符重载
我们这里的赋值运算符重载采用现代写法,还是老样子这里就是我们之前讲的送外卖的例子。
//赋值运算符重载
//s1 = s3
//现代写法
AVLTree<K, V>& operator=(AVLTree<K, V> temp)
{
swap(_root, temp._root);
return *this;
}
AVL树的插入
插入的步骤
AVL树就是在二叉搜素树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么AVL的插入过程可以分为两步:
第一步: 我们需要按照二叉搜索树的方式插入新节点,前面的文章讲过二叉搜索树如何插入新节点,因此这一步对于大家来说问题不大。
第二步: 插入完新节点后,调节节点的平衡因子。这一步是AVL树的重点也是难点所在,我们要想真正知道AVL树是如何插入的,就必须学会如何调节平衡因子。
平衡因子的调节
一个节点的平衡因子是否更新,取决于,他的左右子树的高度是否变化,因此插入一个节点后,这个节点的祖先节点的平衡因子可能需要更新。因此下面我们来说一下祖先节点的平衡因子是如何更新的。
-
首先我们需要判断一下插入的节点是父亲节点的左孩子还是右孩子,如果是父亲节点的左孩子,父节点的平衡因子-1,如果是父节点的右孩子,父节点的平衡因子+1;
-
当我们更新完父亲节点的平衡因子后,此时父节点的平衡因子会有以下的几种情况:
- 当前父节点的平衡因子为0,这说明插入节点之前,父节点的平衡因子为1或者-1,插入后被更新成0,此时表示我们这棵树已经是一棵平衡树了,不需要再向上更新平衡因子了。
- 如果父节点的平衡因子等于1或者-1,说明插入节点之前,父节点的平衡因子为0,插入后被更新成1或者-1,对于上层的节点有影响,因此我们需要继续向上迭代更新祖先节点的平衡因子。
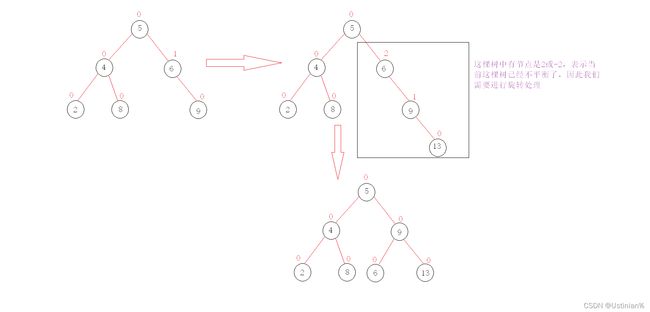
- 如果父节点的平衡因子等于2或者-2,说明插入节点之前,父节点的平衡因子为1或者-1,插入后被更新成了2或-2;此时该父节点的平衡因子违反了平衡树的性质,因此我们需要对它进行旋转处理。
旋转处理(父节点的平衡因子违法平衡树的性质)
我们这里对于旋转处理又分为了以下的四种情况:
-
左单旋
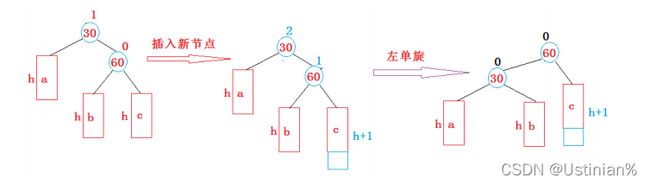
新节点插入到较高右子树的右侧,导致我们的右子树被拉高违反了平衡树的性质。
我们先来看一下左单旋的抽象图:
看完了抽象图之后我们再来看两个左单选的具象图
具象图一:
具象图二:
看完抽象图和具象图之后我们就可以找到左单旋的规律:
将subR的左孩子(subRL)去做parent的右孩子,然后再让parent去做subR的左孩子,更新他们三者之间的链接关系,最后将parent与subR的平衡因子修改为0.
左单旋代码实现:
//左单旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
//将subRL链接到parent的右边
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
//提前记录parent节点的父节点
Node* grandfather = parent->_parent;
//将parent节点链接到subR的左边
subR->_left = parent;
parent->_parent = subR;
//我们这颗树有可能是一个独立的树,也有可能不是因此需要判断一下
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (grandfather->_left == parent)
{
grandfather->_left = subR;
}
else
{
grandfather->_right = subR;
}
//更新subR的父节点
subR->_parent = grandfather;
}
//旋转完毕
//更新平衡因子
subR->_bf = parent->_bf = 0;
}
-
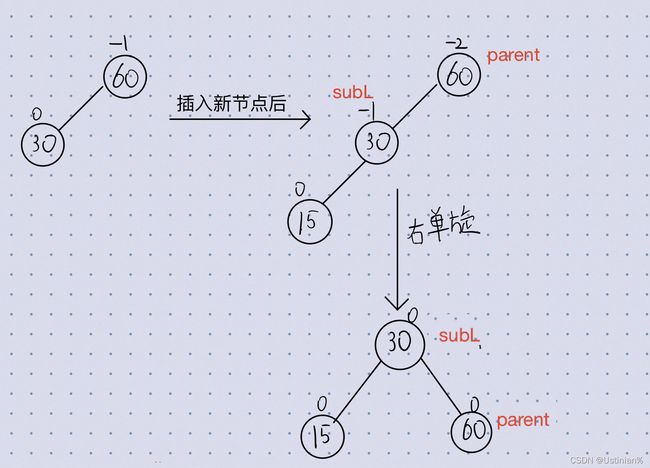
右单旋
新节点插入到较高左子树的左侧,导致我们的左子树被拉高违反了平衡树的性质。
我们先来看一下右单旋的抽象图:
看完了抽象图之后我们再来看两个右单选的具象图
具象图一:
具象图二:
通过观察抽象图和具象图我们也可以找到右单旋有如下规律:
将subL的右孩子(subLR)去做parent的左孩子,然后再让parent去做subL的右孩子,更新三者之间的链接关系,最后将parent与subL的平衡因子修改成0
右单旋实现代码:
//右单旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
//将subLR链到parent的左边
parent->_left = subLR;
//如果subLR不为空,则将subLR的父节点指向parent
if (subLR)
{
subLR->_parent = parent;
}
//提前记录当前parent的父节点
Node* grandfather = parent->_parent;
//让parent节点链接到subL的右边
subL->_right = parent;
parent->_parent = subL;
//我们这棵树有可能是独立的一棵树,也有可能是一棵子树,因此我们需要判断一下
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
//我们先来判断一下parent是grandfather的左孩子还是右孩子
//再来链接subL与grandfather
if (grandfather->_left == parent)
{
grandfather->_left = subL;
}
else
{
grandfather->_right = subL;
}
subL->_parent = grandfather;
}
//旋转完毕
//更新平衡因子
subL->_bf = parent->_bf = 0;
}
-
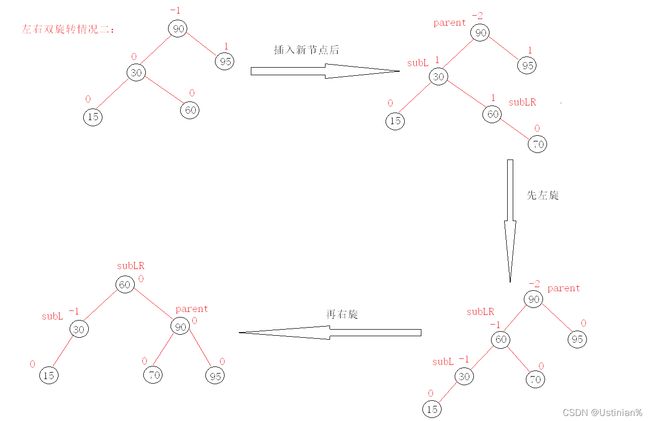
左右双旋
新节点插入较高左子树的右侧—左右:先左单旋再右单旋
我们先来看一下左右双旋的抽象图
看完了抽象图我想和大家说一下其实如果左右双旋如果细分的话它有三种情况,并且左右双旋它也是有它的规律的,我们再来观察一下对应三种情况的具象图并且找一下规律吧。
具象图一:
具象图二:
具象图三:
看完了抽象图以及这三张具象图,不知道大家找到了左右双旋的规律没呢?如果没找到就由我来告诉大家吧
我们通过这些图片可以发现一个规律:
双旋它是一个折线,而单选就是一条直线,左右双旋的本质是让subLR去做根节点,然后将subLR的右孩子给parent做parent的左孩子,将它的左孩子给subL做subL的右孩子。将subLR的右孩子给parent之后parent的平衡因子会变成0,但是subL的平衡因子就会变成-1,同样的将subLR的左孩子给subL之后subL的平衡因子会变成0,但是parent的平衡因子会变成1.
左右双旋代码实现:
//左右双旋
void RotateLR(Node* parent)
{
//提前记录这两个结点以及subLR的bf值
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
//更新双旋后的平衡因子
//如果subLR的bf为1,证明新节点插入在subLR的右边
//最后旋转完subLR是根节点,subLR的右树会给parent做左树
//subLR的左树会给subL做右树
if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
subLR = 0;
}
//如果subLR的bf为-1,证明新节点插入在subLR的左边
else if (bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
subLR = 0;
}
//如果subLR的bf为0,证明新节点就是subLR
else if (bf == 0)
{
parent->_bf = 0;
subL->_bf = 0;
subLR = 0;
}
//如果走到这里说明旋转的时候出问题了,需要去检查一下
else
{
assert(false);
}
}
-
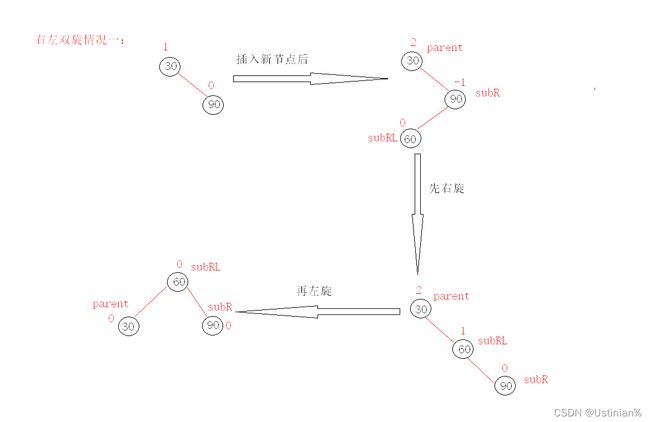
右左双旋
新节点插入较高右子树的左侧—右左:先右单旋再左单旋
我们先来看一下右左双旋的抽象图吧
看完了抽象图我想和大家说一下其实如果右左双旋如果细分的话也有三种情况,并且右左双旋它也是有它的规律的,我们再来观察一下对应三种情况的具象图并且找一下规律吧。
具象图一:
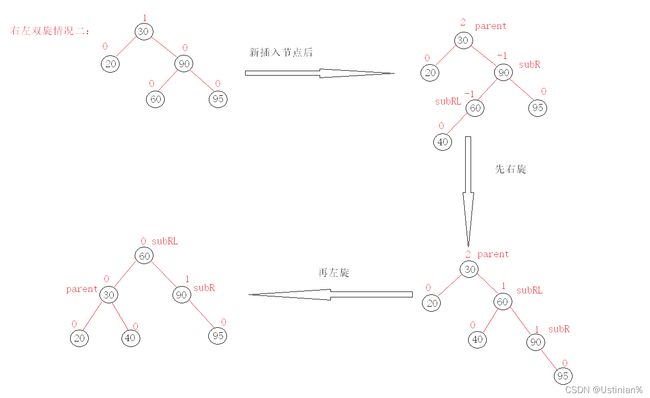
具象图二:
具象图三:
看完了抽象图以及这三张具象图,不知道大家找到了右左双旋的规律没呢?如果没找到就由我来告诉大家吧!!!
我们通过这些图片可以发现一个规律:
双旋它是一个折线,而单选就是一条直线,右左双旋的本质是让subRL去做根节点,然后将subRL的右孩子给subR做subR的左孩子,将它的左孩子给parent做parent的右孩子。将subLR的右孩子给subR之后subR的平衡因子会变成0,但是parent的平衡因子就会变成-1,同样的将subLR的左孩子给parent之后parent的平衡因子会变成0,但是subR的平衡因子会变成1.
右左双旋代码实现:
//右左双旋
void RotateRL(Node* parent)
{
//提前记录这两个结点以及subRL的bf值
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
//双旋转后调节平衡因子
//右左双旋的本质是将subRL的左孩子给parent做右子树
//将subRL的右孩子给subR做左子树
//如果subRL的bf为1,证明新节点插入在subLR的右边
if (bf == 1)
{
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
//如果subRL的bf为-1,证明新节点插入在subLR的左边
else if (bf == -1)
{
parent->_bf = 0;
subR->_bf = 1;
subRL->_bf = 0;
}
//如果subRL的bf为0,证明新节点就是subRL
else if (bf == 0)
{
parent->_bf = 0;
subR->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
代码实现
//插入
pair<Node*, bool> Insert(const pair<K, V>& kv)
{
//如果当前AVL树是一颗空树
if (_root == nullptr)
{
_root = new Node(kv);
return make_pair(_root, true);
}
Node* parent = _root;
Node* cur = _root;
//先找到要插入的地方
while (cur)
{
//如果当前结点的值比插入的值要小
//就去当前结点的右树找插入的地方
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
//如果当前结点的值比插入的值要大
//就去当前结点的左数找插入的地方
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
//如果发现AVL里面有相等值
//返回false
else
{
return make_pair(cur, false);
}
}
//循环结束,cur走到要插入的地方
cur = new Node(kv);
//因为经过下面调整平衡因子之后,cur有可能会改变
//因此我们提前记录一下
Node* newnode = cur;
//判断一下cur的first比parent的值大还是小
//如果大就插入在parent的右边
//反之插入到parent的左边
//我们这里是三叉链
//我们还需要把cur的parent指向parent
if (parent->_kv.first > cur->_kv.first)
{
parent->_left = cur;
cur->_parent = parent;
}
else
{
parent->_right = cur;
cur->_parent = parent;
}
//一个节点的平衡因子是否更新,取决于,他的左右子树的高度是否变化
//插入一个节点,这个节点的祖先节点的平衡因子可能需要更新
//更新平衡因子
while (parent)
{
//1.新增节点在parent的右边,parent->bf++;
if (cur == parent->_right)
{
parent->_bf++;
}
//2.新增节点在parent的左边,parent->bf--;
else
{
parent->_bf--;
}
//平衡因子为0,停止更新
if (parent->_bf == 0)
{
break;
}
//如果parent的平衡因子等于1 or - 1,继续往上更新
else if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = parent->_parent;
}
//如果parent的平衡因子等于2 or -2,已经出现不平衡,需要旋转处理
else if (parent->_bf == 2 || parent->_bf == -2)
{
if (parent->_bf == -2)
{
//右单旋
//if (parent->_left->_bf == -1)
if (cur->_bf == -1)
{
RotateR(parent);
}
//左右单旋
//cur->_bf == 1
else
{
RotateLR(parent);
}
}
//parent->_bf == 2
else
{
//左单旋
//if (parent->_right->_bf == 1)
if (cur->_bf == 1)
{
RotateL(parent);
}
//右左单旋
//cur->_bf == -1
else
{
RotateRL(parent);
}
}
//调整后变成了平衡树,bf为0,不需要调整了
break;
}
//如果平衡因子不是上面的那些,那么就证明我们的平衡因子出错误了需要去检查一下
else
{
assert(false);
}
}
return make_pair(newnode, true);
}
[]运算符的重载
上面我们实现了AVL树的Insert之后,我们就可以来实现以下[]运算符的重载了
我们实现[]运算符是为了让AVL可以向数组那样去访问或者修改元素
这里的Insert插入会返回一个pair类,pair类中的first类型存放的是当前节点的指针,pair的second类型存放的是一个bool值如果插入成功bool值为true,反之为false
返回的pair类我们用ret去接收,如果插入成功,ret的first会存放当前节点的指针,second就是true,如果插入失败了ret的first会存放当前节点的指针,second就是false。
因此不管最后插入成功与否我们只需要返回当前节点指针中kv(也是一个pair)的第二个类型即second即可。
//[]重载
V& operator[](const K& key)
{
pair<Node*, bool> ret = Insert(make_pair(key, V()));
return ret.first->_kv.second;
}
注:这里的pair是一个类模板,make_pair是一个函数模板,我们在make_pairt中给数据,它就会根据这两个数据自己去推导然后生成对应类型的pair类
AVL树的查找
AVL树的查找和二叉搜索树的代码基本一致,我们这里不做过多的介绍(具体二叉搜索树中有讲)
//查找
Node* find(const K& key)
{
if (_root == nullptr)
{
return nullptr;
}
Node* cur = _root;
while (cur)
{
//如果当前结点的key值大于要查找的key
//往左树去查找
if (cur->_kv.first < key)
{
cur = cur->_left;
}
//往右树中去查找
else if (cur->_kv.first > key)
{
cur = cur->_right
}
//找到了
else
{
return cur;
}
}
return nullptr;
}
AVL树的打印
因为AVL树它也是一棵二叉搜索树,因此我们想打印这颗AVL树只需要采用中序遍历的方式去打印就可以得到这棵树中所有元素按照从小到大排序的结果。
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}
//中序遍历
void InOrder()
{
_InOrder(_root);
}
验证是否为AVL树
我们上面写了那么多代码,但是我们怎么知道我们这颗树到底是不是AVL树呢?
因此我们就需要去写一个函数来判断以下当前AVL树是否为AVL树才行
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
- 验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
- 验证其为平衡树
- 每个节点子树高度差的绝对值不超过1
- 节点的平衡因子是否计算正确(右树高度-子树高度是否等于当前节点的平衡因子)
代码实现
//求当前这节点的高度
int Height(Node* root)
{
if (root == nullptr)
{
return 0;
}
//左子树的高度
int leftHeight = Height(root->_left);
//右子树的高度
int rightHeight = Height(root->_right);
//当前结点的高度等于
//左子树与右子树中高度最大的那个 在+1
return max(leftHeight, rightHeight) + 1;
}
bool _IsBalance(Node* root)
{
//如果是空树,我们认为它是平衡的
if (root)
{
return true;
}
int leftHeight = Height(root->_left);
int rightHeight = Height(root->_right);
//如果右树高度减去左树高度不等于当前节点的平衡因子
//我们这颗树则不是平衡的
if (rightHeight - leftHeight != root->_bf)
{
cout << "平衡因子异常:" << root->_kv.first << endl;
return false;
}
//平衡树的右数高度减去左树高度应小于2
//并将当前节点的左子树与右子树都要是平衡树
//这棵树才算是平衡树
return abs(rightHeight - leftHeight) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
//判断是否为AVL树
bool IsAVLTree()
{
return _IsBalance(_root);
}
实例演示:
void TestAVLTree()
{
//int a[] = { 1, 3, 5, 7, 6 };
//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
AVLTree<int, int> t;
for (auto e : a)
{
t.Insert(make_pair(e, e));
cout << "插入" << e << "->" << "是否为AVLTree" <<":"<< t.IsAVLTree() << endl;
}
t.InOrder();
}
运行结果:
AVL树代码实现
#include以上就是AVL树的所有内容了,对于AVL树这块如果大家想弄清楚一定要多画图多敲敲代码。如果觉得作者的文章还不错的话,可以三连支持一下作者。