机器学习笔记(1) 逻辑回归
机器学习笔记(1) 逻辑回归
0.前言介绍
逻辑回归,是一种二元分类算法 ,其主体思想还是继承了线性回归。逻辑回归与之后的神经网络有着千丝万缕的联系,经常被用来当神经元激活算法讲,所以吴恩达教授的deep learning也是从逻辑回归开始入手,其重要性不容小觑。
相信大家在高中都与线性回归有所纠缠,那逻辑回归用大白话讲,就是把线性回归的结果做一个分段。我们知道线性回归最后的结果是一个连续的量,是一个数值,我们如何把一个回归算法用到分类中呢,最简单的办法就是设定阈值,高于阈值的算作一类,低于阈值算作另一类,这就是逻辑回归的基础思想,即把连续的量打散,变成离散的类别。
好了,就像我们之前说过的,要学习一个算法,从三方面入手:算法结构,代价函数,更新策略。
1.算法结构
首先是算法结构。我们知道线性回归的结构是 y = W x + b y=Wx+b y=Wx+b ,即一般线性表达式。然而在逻辑回归中,我们的输出值只有两个,就是1和0,因为逻辑回归是一个二分类问题,所以结果只有两个类别。所以我们要把本来定义在 R R R上的 y y y放缩到区间 [ 0 , 1 ] [0,1] [0,1]上,这样,我们的因变量就可以看作是描述分类的一个概率值,也就是说,因变量越接近0,那么原物品属于0所代表的类别的概率就越大,反之亦然。
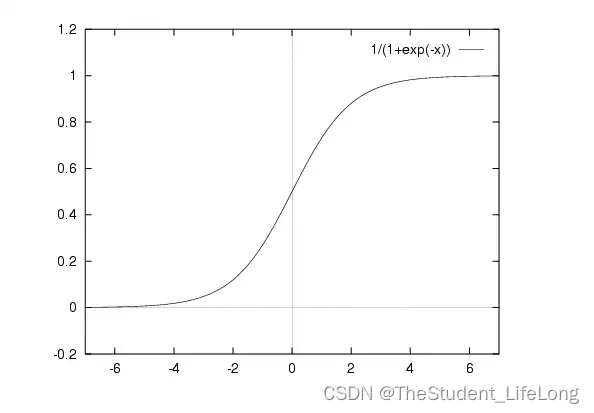
那么如何进行放缩呢,我们引入机器学习领域的重要函数:sigmoid函数。其表达式为:
s i g m o i d ( x ) = 1 1 + e − x sigmoid(x) = \frac {1}{1+e^{-x}} sigmoid(x)=1+e−x1
其图像如下图:
图1.1
我们可以观察到,任何实数域自变量都被映射到了 [ 0 , 1 ] [0,1] [0,1]区间上,现在我们可以写出逻辑回归的表达式:
y ^ = σ ( W x + b ) \hat{y} = \sigma(Wx+b) y^=σ(Wx+b)
其中 σ 函数即为 s i g m o i d 函数 \sigma函数即为sigmoid函数 σ函数即为sigmoid函数,整个式子就是把线性回归的表达式做一次sigmoid映射,最后得出的 y ^ \hat{y} y^即为预测结果。
2.代价函数
Cost function,意即代价函数,也有教材翻译作成本函数,表示我们的预测值与真实值的差距。一般的线性回归中,我们使用方差的形式来度量整个差距,所以高中求解线性回归的方法也叫作最小二乘法,一般如下表示:
J ( W , b ) = 1 m ∑ 0 n ( y i ^ − y i ) 2 J(W,b)=\frac{1}{m}\sum_0^n(\hat{y_i}-y_i)^2 J(W,b)=m1∑0n(yi^−yi)2
这里,我们还需要明确一个概念,以防读者在阅读其他教材时产生歧义。Loss function,也称为error function,翻译过来叫损失函数,它与代价函数有什么区别呢?损失函数表示一个样本点上的预测偏差,代价函数表示整个样本集的预测偏差,例如,上述的方差代价函数,写作损失函数为:
L o s s ( y ^ , y ) = ( y ^ − y ) 2 Loss(\hat{y},y) = (\hat{y}-y)^2 Loss(y^,y)=(y^−y)2
当然有些国内教材也不区分以上概念,读者了解即可。
言归正传,然而,我们的逻辑回归并不采取以上代价函数,因为这会产生凸优化问题,这一块的知识涉及大量数学原理,我们不展开讲,这里我们只大概阐释一下原因,读者有兴趣可以自行查阅其他文献。凸优化,通俗来说是找到使代价函数最小的参数的过程,我们机器学习领域一般使用梯度下降法来求解最优参数,也就是根据导数找极值点。方差型代价函数的图像一般是这样的:
图1.2
由图可得,该函数有非常多的极值点,算法难以找到最小的点,所以这就叫凸优化问题。那么如何解决呢,科学家们提出了另一种代价函数用于逻辑回归算法,一般认为该函数图像为标准凸函数,表示如下:
J ( W , b ) = − 1 m ∑ 0 n [ y i l n y i ^ + ( 1 − y i ) l n ( 1 − y i ^ ) ] J(W,b)=-\frac{1}{m}\sum_0^n[y_iln\hat{y_i}+(1-y_i)ln(1-\hat{y_i})] J(W,b)=−m1∑0n[yilnyi^+(1−yi)ln(1−yi^)]
也就是说
L o s s ( y ^ , y ) = y l n y ^ + ( 1 − y ) l n ( 1 − y ^ ) Loss(\hat{y},y)=yln\hat{y}+(1-y)ln(1-\hat{y}) Loss(y^,y)=ylny^+(1−y)ln(1−y^)
读者肯定会问了,这是怎么推导出来的呢?我们粗略讲解一下。
不妨设 y ^ \hat{y} y^为y等于1的概率,为什么可以这么设?因为我们知道y只有两个取值,1或0,那么
当y=1时, P ( y ) = y ^ P(y)=\hat{y} P(y)=y^
当y=0时, P ( y ) = 1 − y ^ P(y)=1-\hat{y} P(y)=1−y^
这里读者可以把 P ( y ) P(y) P(y)看作预测正确的概率,专业一点称作最大似然值估计,我们希望这个概率尽可能地大,这是好理解的,因为y取1时,我们希望 y ^ \hat{y} y^尽可能地大,反之亦然。这个分段函数还是太复杂,我们把它整合到一个式子里,也就是:
P ( y ) = y ^ y ( 1 − y ^ ) ( 1 − y ) P(y)=\hat{y}^y(1-\hat{y})^{(1-y)} P(y)=y^y(1−y^)(1−y)
读者可自行验证,上式与之前的分段函数是等价的。
然后我们对这个概率函数取对数,就得到了损失函数的相反数:
y l n y ^ + ( 1 − y ) l n ( 1 − y ^ ) yln\hat{y}+(1-y)ln(1-\hat{y}) ylny^+(1−y)ln(1−y^)
为什么说是相反数,因为我们希望代价函数尽可能地小,这时概率P应该尽可能地大,所以两者是负相关的,所以我们在式子之前加一个负号,再求平均数,就得到了之前给出的代价函数式子。
3.更新策略
这里的更新策略就是我们之前讲过的梯度下降法,这一块内容我不打算讲的太详细,因为笔者认定读者们都掌握了求导的基本法则,并且对复合函数的链式法则也能熟练运用。
我先介绍一下更新的思路,我们求得代价函数的值之后,求各个参数的偏导数,也就是分别以各个参数为自变量求导,求得导数后,用原参数值减去对应偏导数与学习率的乘积,得到新的参数值。学习率是什么东西,读者不必纠结,后面的笔记会详细解释,这里读者只要知道学习率是一个介于0和1的小数即可。
以逻辑回归为例,写一下更新策略的过程:
首先求导:
d J d σ = − y y ^ + 1 − y 1 − y ^ \frac{dJ}{d\sigma}=-\frac{y}{\hat{y}}+\frac{1-y}{1-\hat{y}} dσdJ=−y^y+1−y^1−y
如果忘记上式字母都是什么意思可以翻到前面复习一下,这实际就是sigmoid函数的导数。
然后:
d z = d J d ( W x + b ) = y ^ − y dz=\frac{dJ}{d(Wx+b)}=\hat{y}-y dz=d(Wx+b)dJ=y^−y
d J d W = x d z \frac{dJ}{dW}=xdz dWdJ=xdz
d J d b = d z \frac{dJ}{db}=dz dbdJ=dz
然后进行更新:
W = W − α d J d W W=W-\alpha \frac{dJ}{dW} W=W−αdWdJ
b = b − α d J d b b=b-\alpha \frac{dJ}{db} b=b−αdbdJ
更新完毕!现在你获得了新的参数,但现在我们并不一定找到了最优解,我们需要重复以上过程很多次,也就是计算预测值->更新参数->计算预测值->更新参数…直到最后我们求得的导数,也就是梯度,小于某一阈值,说明代价函数渐渐趋于平缓,那么我们可能已经找到最优解了。
4.最后
恭喜你!看完了本篇笔记,相信对很多初次接触机器学习的人来说,还是会感觉懵懵的,但是没关系,坚持就是胜利!这里我推荐吴恩达教授的机器学习和深度学习系列课程作为入门,推荐《机器学习的数学》(雷明著)和《机器学习的数学原理和算法实践》(大威编著)作为参考书。我们一起加油!!!
相关电子书资源,欢迎关注笔者微信公众号:白日梦手帐
参考资料
1.《机器学习》(周志华)
2.《机器学习的数学》(雷明)
3.《机器学习的数学原理和算法实践》(大威)
4.《deep learning》(吴恩达)
5.《machine learning》(吴恩达)