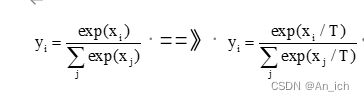训练和部署之间的区别-模型压缩

神经网络训练

神经网络训练的本质就是找到一个f(x),只不过是一个参数量很大的f(x)

那么神经网络训练和部署之间的区别就是减少参数量

为什么要减少参数量

1.大模型不方便进行部署，网络的推断速度比较慢

2.对于移动端等设备也没有这么强的算力

3.对于网络训练的结果，也就是网络训练中学习到的知识和网络参数量两者的关系不是线性的，知识和参数量之间的关系更趋向于一个log函数

怎样减少参数量

1.减小参数的精度

例如将参数的64位精度减小为32位

2.参数的clustering

这一步就等同于参数的池化

3.对参数进行Huffman Coding

所谓Huffman Codiing（哈夫曼编码）就是对参数依据出现的概率进行编码，出现频率高的用短编码，出现频率低的用长编码

Huffman Coding

例如aaaasssdffg

一种特殊的二叉树，每次先将出现频率最低的两个元素进行合并

先合并d,g，然后根据出现的频率依次为f,s,a

d:1110

g:1111

f:110

同理可推出剩下的元素编码

4.模型的剪枝

剪枝的思想：

剔除不必要的参数而不会对模型的效果产生较大的影响

步骤：

首先剔除掉不必要的参数，其次对模型进行重新训练（retrain）来恢复模型性能

方法：

1.单个权重（weight）剪枝：

        对损失函数增加惩罚项（L1,L2范数）让权重的值减小，再通过设置阈值的方法去除掉小于阈值的参数

2.单个神经元（neuro）剪枝：

        通过APP统计多次输出为0的神经元进行去除

一般情况下使用对单个神经元进行剪枝：因为对单个权重进行剔除后会导致特征矩阵的形状发生变化，要保持形状不变需要进行补零操作，而剔除单个神经元相当于进行dropout

为什么不直接进行训练小模型？

为什么要对大模型训练进行剪枝操作后再对小模型进行retrain，而不是选择直接对小模型进行训练？两者的训练结果一样吗？

首先两者的训练结果是不一样的。

为什么会不一样呢？

一种是经过大模型训练后剪枝的小模型进行retrain（a方法）

一种是直接对小模型进行训练（b方法）

区别在于对小模型进行训练的初始化参数不一样，a方法使用大模型训练后找到的最优参数，使用最优参数初始化重新训练得到的结果，具有和大模型相似的性能。b方法重新进行初始化，训练结果很糟糕。

所以两者的区别在于是否有大模型去圈定参数的范围，可以理解为a方法已经大致确定函数用到的参数了，留下的都是有用参数，b方法从头开始训练参数。

对单个神经元剪枝和dropout的区别是什么？

1.对单个神经元进行剪枝是训练后的操作，dropout是训练过程中的操作

2.对单个神经元的剪枝是经过挑选的，多次输出为0的神经元，而dropout是在训练过程中随机对神经元进行剔除。

5.模型结构重构

1.将较大的矩阵进行分解转化为较小的几个矩阵

2.利用CNN进行降维

这个方法没怎么看懂，以后再看看

6.知识蒸馏（KD）

Distilling the Knowledge

这种方法就是有一个老师模型（teacher-model）还有一个学生模型（student-model）

适合分类问题，也就是说神经网络的最后一层为softmax

老师模型(t-model):进行原始模型的训练

学生模型(s-model):进行精简模型的训练

这个t-model是比较复杂的模型，s-model为比较简单的模型

对模型是什么网络没有要求，总之一个复杂一个简单。

简单s-model模型去学习复杂t-model模型的softmax的概率分布，以此将t-model的泛化能力转移到s-model

为什么学习softmax的概率分布就能获得复杂模型的泛化能力呢？

因为softmax输出的是每一个类别的概率：[0.9(猫)，0.05（狗），0.05（人）]，是一种soft-target其中包含大量的信息。这个特性不同于one-hot这种hard-target，每一种编码就代表一种类别，比如[1,0,0]就是代表猫

one-hot        hard-target        [1,     0,      0]

KD                soft-target        [0.9,0.05,0.05]

在理解s-model怎么获得t-model的概率分布之前先了解一个超参数

知识蒸馏-温度T

 

 温度T:
原始的softmax就是T=1时的特殊情况

温度T越高，softmax上各个值得分布就越平均

不管温度T怎么样，soft-target都有忽略掉小的P所携带信息得倾向

温度T的作用是啥：

温度T其实就是用来软化标签的。所谓硬标签指的是one hot向量，这样的标签里面只有一个信息，就是这个分类是A而不是B。但teacher网络的预测并不是one hot向量而是一个概率值，如果这个概率中有类似这样的[0.6, 0.3, 0.05, 0.05]那么说明这个图片的分类是第0类但与第1类更接近，与第2和第3类并不接近。这就是软标签的概念，为了给网络提供更多的信息。但一个训练好的网络，它对于很多物体的分类是很确定的，它的输出大部分都会是[0.98, 0.01, 0.006, 0.0004] 这样的，这样的标签更接近硬标签。而温度T加在这样的标签上，就会使teacher的标签没有那么硬，让置信度高的降低一些，低的升高一些，将刚才的输出对应转化为[0.7, 0.2, 0.12, 0.08]这样的(只是举例，数值没有仔细计算)，从而提供更多的信息给student。从另一个角度讲，加入了温度T的teacher是一个弱化了的teacher，避免teacher过强导致学习学不进去。
另外蒸馏的过程中需要对T逐渐降温，最终的使T=1，p=q的时候没有loss。如果一直保持较高的温度是不能得到好的结果的。

Hinton论文知识蒸馏里面的温度T到底是干什么用的？ - 奇思的回答 - 知乎 https://www.zhihu.com/question/286722210/answer/2210154752/

困了，明天再写

2023-6-18 23：22

okey，继续

s-model怎么获得t-model的概率分布

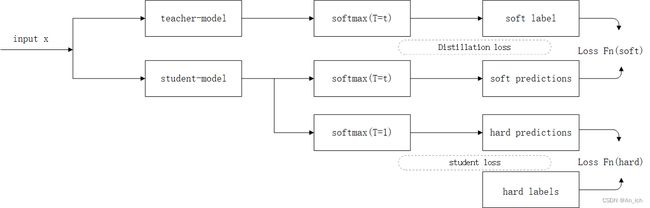
1.由teacher-model得到t-soft labels（p）

2.由student-model得到s-soft lables（q）

3.由t-soft labels和s-soft lables得到交叉熵损失函数（loss-soft）

4.在student-model，在T=1时得到hard prediction（h）

5.将hard prediction和真实分类（g）得到交叉熵损失函数（loss-hard）

 6.将loss-soft和loss-hard加权相加得到最终的loss

 为什么损失函数要选择交叉熵呢

这是一个老生长谈的问题，为啥分类问题里面会用到交叉熵损失，而不用平方损失呢？ 既然sigmoid输出的是概率值，难道用这个概率值与真实的label0或者1求平方损失，然后更新参数不可以吗？

对loss值求偏导就可以很好的解释这个问题

对MSE求偏导：

对cross-entropy求偏导：

 对于梯度更新的公式：

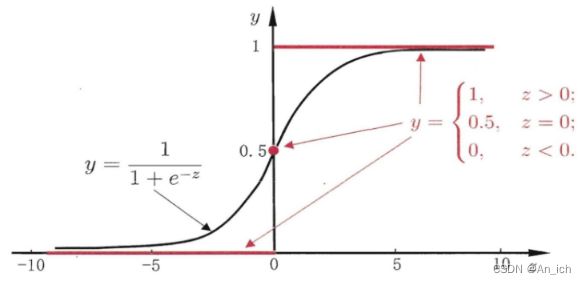
 再结合sigmoid图像可以得到：

当MSE求偏导后剩下的是sigmoid的导数，他在预测的输出结果比较大时，对参数的更新是很小的

 而使用cross-entropy求导后剩下的是sigmoid函数，可以保证对于参数的更新

 (8条消息) 【超详细公式推导】关于交叉熵损失函数（Cross-entropy）和 平方损失（MSE）的区别_交叉熵损失函数 exp_苏学算法的博客-CSDN博客

(8条消息) 为什么均方差（MSE）不适合分类问题？交叉熵（cross-entropy）不适合回归问题？_交叉熵和mse可以一起使用吗_this_is_part_of_life的博客-CSDN博客

多提一嘴准确率和召回率的区别：

准确率：你认为是对的所有样本中有多少个是真正正确的

召回率：在样本中一共有多少个是正确的你召回了多少