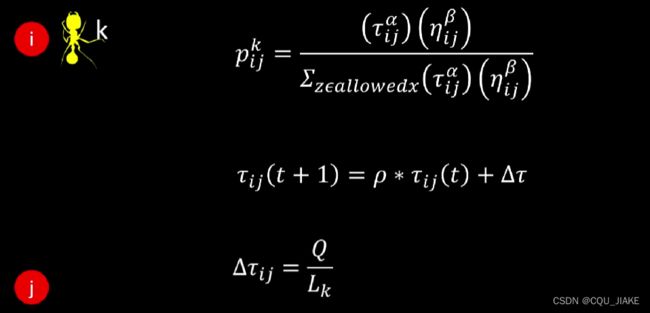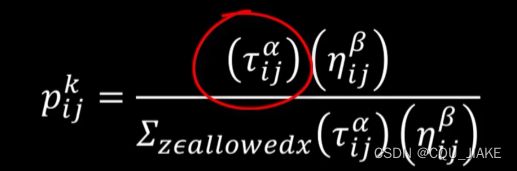1.23聚类算法（kmeans(初始随机选k，迭代收敛）,DBSCAN（dij选点），MEANSHIFT（质心收敛），AGENS(最小生成树）），蚁群算法（参数理解、过程理解、伪代码、代码）
聚类算法
聚类结果不变
K-means
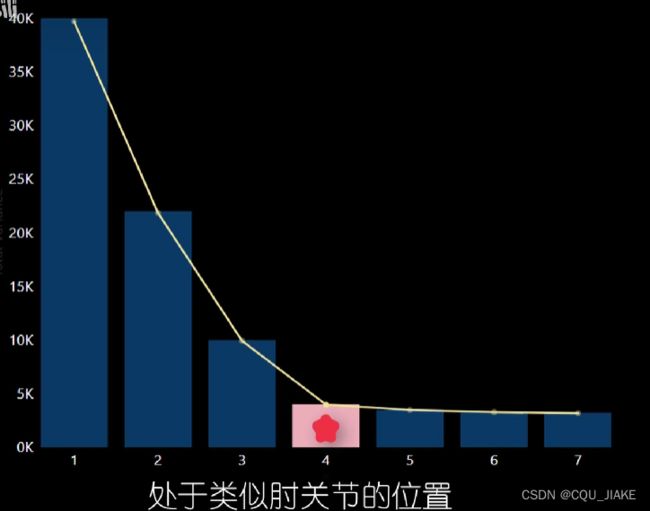
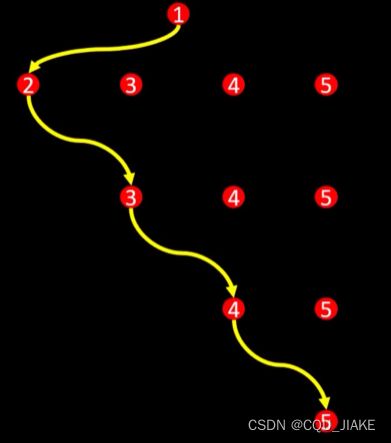
K值是事先确定好的，是要划分的聚类的数量；初始时随机选择k个点，然后逐渐选择离他最近的点，不断锁定最近的，最后计算方差和；这个是轮流的
这个就类似于模拟退火的思想
当前聚类下的方差和，也称为簇内方差（within-cluster variance），是一种度量聚类质量的指标。它衡量了簇内数据点与各自簇中心的差异程度。方差和越小，表示簇内的数据点越紧密聚集在一起。
计算当前聚类下的方差和的一种常见方法是使用平方欧氏距离（squared Euclidean distance）。具体计算步骤如下：
1. 对于每个簇，计算该簇内所有数据点与簇中心的平方欧氏距离。
2. 将每个簇内所有数据点与簇中心的平方欧氏距离求和。
3. 将所有簇的平方欧氏距离之和作为当前聚类下的方差和。
简化的计算公式如下：
方差和 = Σ(Σ(欧氏距离^2))
其中，Σ表示求和操作，欧氏距离^2表示欧氏距离的平方。
需要注意的是，方差和的计算可能因聚类算法而异，所以在具体应用中，请参考所使用的聚类算法的文档或相关资料，了解更准确的计算方法。
要确定K值，采用肘方法
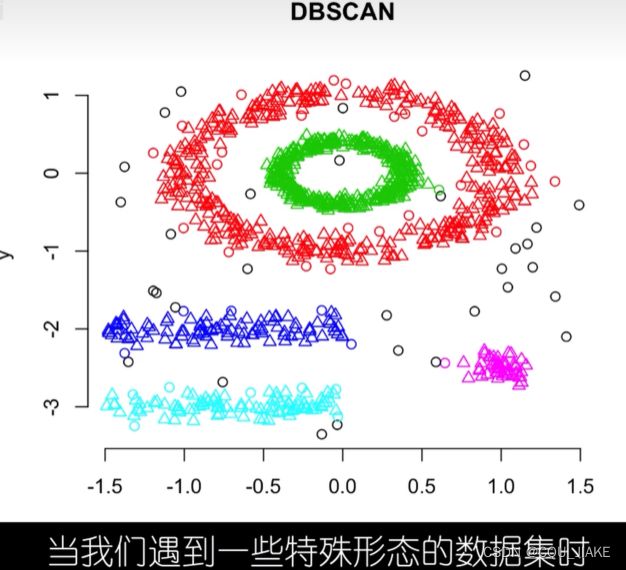
DBSCAN
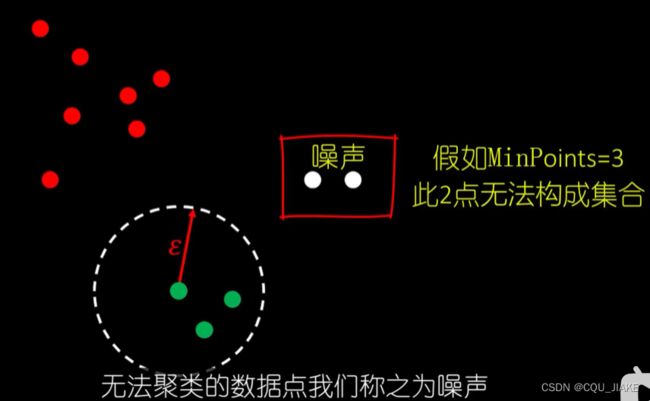
带噪声的聚类
两个参数
一个是距离参数，一个是最少点数；就是先从某点（随机点）出现，然后以这个点为圆心向周围辐射，辐射大小是距离参数，之后再以确定的点去确定其他点，就是dij的一个过程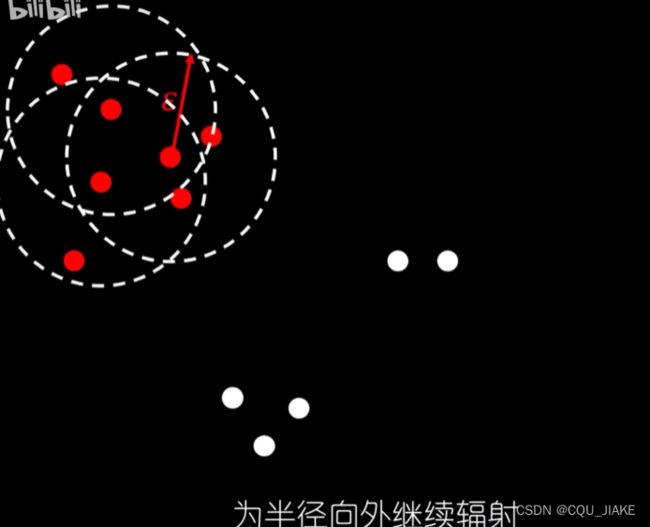
MEANSHIFT均值漂移算法 
先选一个半径为r的分析区域， 计算质心，然后以质心为圆心再计算，迭代一定次数后最终趋向于最终最密集的地方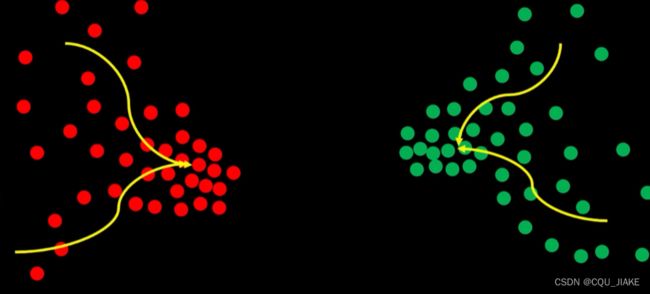
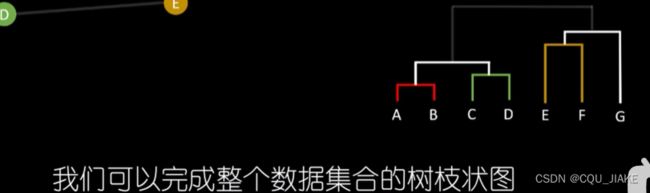
AGNES集聚分层聚类算法
能保证最近的两点归于同一组
纵坐标为对应的聚类距离临界值
就是相当于最小生成树的p算法，只不过在相连的时候，如果边的权值大于聚类距离临界值了，就不练了，就作为新的聚类连通图。重复这个过程直到所有点
最优路径问题，蚁群ACO
三个参数，阿尔法，β，挥发系数ρ值
当阿尔法为0时，弗洛蒙浓度不起作用，完全根据城市距离做选择 
当β为0时，完全依据弗洛蒙浓度做判断
再回顾
Tao为弗洛蒙浓度
总路程越短，Δtao就会越大
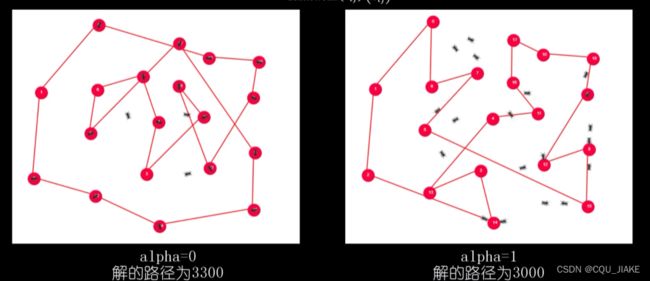
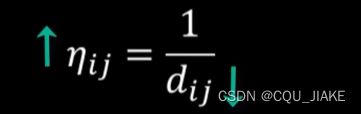两城市距离越小，η值越大，就是说依据图自身的特点，即每一点上的局部最优解，如果阿尔法等于1，就是完全依据每一步的最优解
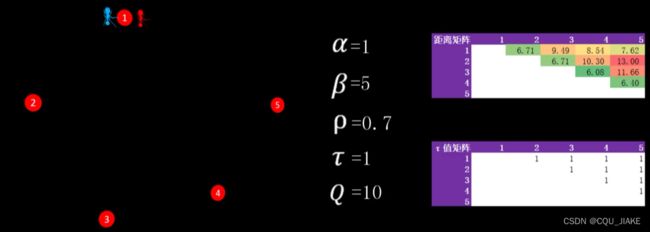
参数汇总理解
阿尔法是弗洛蒙浓度的控制系数（对上个最优全局做控制），
β是距离的控制（针对局部最优），
ρ是挥发系数（同样控制上个全局最优对下次搜索的影响程度，即继承上次的多少弗洛蒙浓度），Q同样是控制上个全局对下次的影响（即下次在上次继承的一部分基础上，又多了多少，Q来控制这个），
tao就是初始的弗洛蒙初值
就是说α控制上次对这次的影响，α越大，则影响越大，越容易形成路径依赖，越不容易找到潜在的可能最优解，就会使后来每次都越来越走一样相同的最开始走的路，即所谓快速收敛；
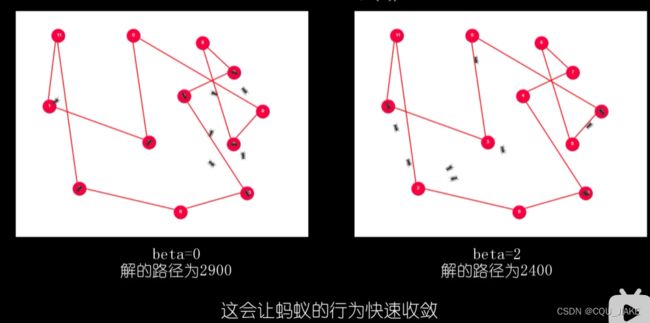
β是控制每次路径长短对本次的影响，β越大，则越倾向于局部最优，蚂蚁就越短视，越容易倾向于走更短的路径，也越不容易找到潜在的可能的最优解，即每次都会犯同样的短视错误。
过程理解
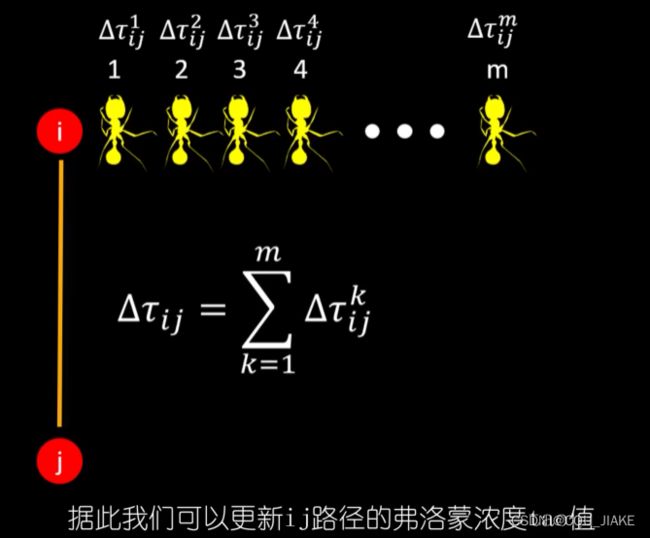
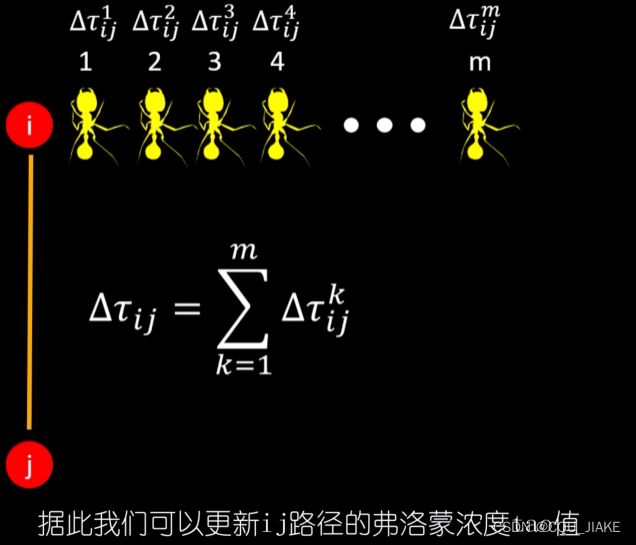
初始时，就是各个路的弗洛蒙浓度都是一样的，然后一开始就是遵循局部最优，路径短的有更大概率会被选上，有好多蚂蚁走好多不同的路径，然后在下一轮迭代中，依据每只蚂蚁走的总路径长度，在其所走过的路径上增加弗洛蒙浓度，由于是最后走完后计算的，所以会体现出这个走的路的全局的一个性质，全局路径越短，增加的弗洛蒙越多，全局路径越长，增加的就越少，在下次迭代走的概率就会相对减少；然后在下次迭代中，之前走的路径里弗洛蒙浓度越大，说明沿这条路走的整体路径会越小，相对于其他弗洛蒙浓度小的路径而言，被走的概率会越大；但也会考虑到在这个路径基础上的，其他稍短路，所以就是一个概率的东西，经过多次迭代找到最好的
代码、伪代码
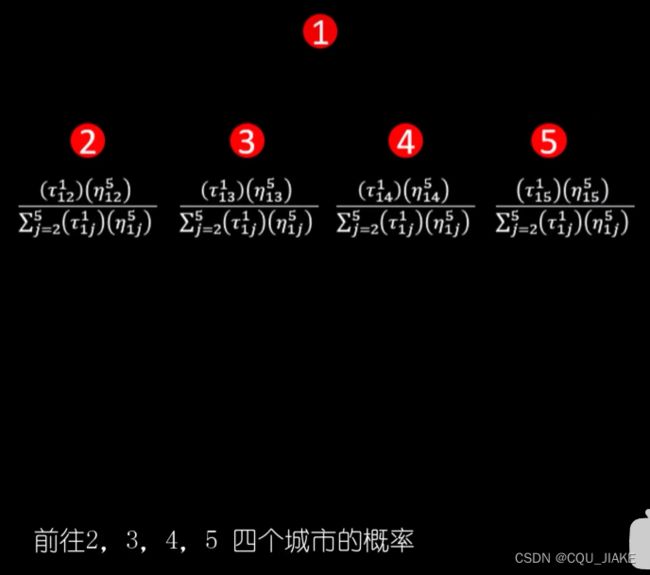
就是预设迭代n次，然后每次都有m个蚂蚁，然后每个蚂蚁在其此时各自的起点上，依据概率公式，去选择下一个终点，并加在它的路径长度上；
最后蚂蚁都走完了，就依据蚂蚁走的路径去更新弗洛蒙矩阵，并判断、保留最短路径
这个弗洛蒙矩阵的作用主要就体现在每次蚂蚁的下一个路径选择上
import numpy as np
class AntColonyOptimization:#蚂蚁类定义
def __init__(self, num_ants, num_iterations, pheromone_decay, alpha, beta):#构造函数
self.num_ants = num_ants#蚂蚁数量、列表
self.num_iterations = num_iterations#迭代次数
self.pheromone_decay = pheromone_decay#衰减系数ρ
self.alpha = alpha#弗洛蒙控制系数，全局控制系数，越大越容易形成路径依赖
self.beta = beta#图自身特点控制系数
def optimize(self, distance_matrix):
num_cities = distance_matrix.shape[0]#可选城市矩阵
self.pheromone_matrix = np.ones((num_cities, num_cities))#弗洛蒙矩阵
best_path = None
best_distance = np.inf
for iteration in range(self.num_iterations):#迭代完，循环里每次都是一次迭代
ant_paths = self.construct_ant_paths(distance_matrix)#构建、获取每次迭代里，m只蚂蚁走的路径，就是蚂蚁群的路径矩阵
self.update_pheromone_matrix(ant_paths)#在所有蚂蚁走完后，依据其所走的路径，更新弗洛蒙矩阵，主要是加上新增的弗洛蒙浓度
current_best_path, current_best_distance = self.get_best_solution(ant_paths, distance_matrix)#获取这次迭代中所有蚂蚁走出来的最好路径总长与最好路径
if current_best_distance < best_distance:#获取更新最优
best_path = current_best_path
best_distance = current_best_distance
self.pheromone_matrix = (1 - self.pheromone_decay) * self.pheromone_matrix#更新弗洛蒙矩阵，是进行挥发衰减
return best_path, best_distance#最后返回迭代完成后的最短路与最短路径
def construct_ant_paths(self, distance_matrix):
num_cities = distance_matrix.shape[0]
ant_paths = []
for ant in range(self.num_ants):#这个是让每只蚂蚁都完成一次路径，是一个循环语句，每次循环内部是对一只蚂蚁进行操作
visited_cities = []
current_city = np.random.randint(num_cities)#开始起点随机，不影响最终结果的最短
visited_cities.append(current_city)
while len(visited_cities) < num_cities:#循环，直到走完所有城市
next_city = self.select_next_city(visited_cities, distance_matrix)#依据弗洛蒙矩阵与距离矩阵与以遍历的，综合考量，随机选择下一个城市走
visited_cities.append(next_city)#加入已遍历城市，下次不再遍历
current_city = next_city#更新当前城市
ant_paths.append(visited_cities)#这个蚂蚁走完后，在本次迭代中加入它所走的路径
return ant_paths#最后返回本次迭代中所有蚂蚁走的路径
def select_next_city(self, visited_cities, distance_matrix):#每个蚂蚁在其各自起点的基础上，概率选择下一个终点
num_cities = distance_matrix.shape[0]
current_city = visited_cities[-1]#获取访问城市的最后一个元素，即此时的起点
unvisited_cities = [city for city in range(num_cities) if city not in visited_cities]
probabilities = []
for city in unvisited_cities:#遍历还没访问过的城市，获取访问这些城市的概率
pheromone = self.pheromone_matrix[current_city, city]#得到到这个城市路径上的弗洛蒙浓度
distance = distance_matrix[current_city, city]#得到到这个城市的距离
probability = pheromone**self.alpha * (1/distance)**self.beta#计算得到到这个城市的概率
probabilities.append(probability)#加入到这个城市的概率进列表里
probabilities = np.array(probabilities)
probabilities /= np.sum(probabilities)#归一化
next_city = np.random.choice(unvisited_cities, p=probabilities)#随机选择一个城市，依据概率矩阵
return next_city#返回最后选择的城市
def update_pheromone_matrix(self, ant_paths):
num_cities = self.pheromone_matrix.shape[0]
for ant_path in ant_paths:#遍历蚂蚁群的每只蚂蚁所走过的路径
for i in range(num_cities - 1):#得到这个蚂蚁路径上的城市
current_city = ant_path[i]
next_city = ant_path[i + 1]#联通这个蚂蚁所选择的路径
self.pheromone_matrix[current_city, next_city] += 1#弗洛蒙增量，增加1
def get_best_solution(self, ant_paths, distance_matrix):
best_path = None
best_distance = np.inf
for path in ant_paths:#得到蚂蚁群的每只蚂蚁走的路径
distance = self.calculate_path_distance(path, distance_matrix)#计算这只蚂蚁路径的长度
if distance < best_distance:
best_path = path
best_distance = distance
return best_path, best_distance
def calculate_path_distance(self, path, distance_matrix):
distance = 0
for i in range(len(path) - 1):
current_city = path[i]
next_city = path[i + 1]
distance += distance_matrix[current_city, next_city]
return distance
# 示例用法
distance_matrix = np.array([[0, 2, 9, 10],
[2, 0, 6, 4],
[9, 6, 0, 8],
[10, 4, 8, 0]])
aco = AntColonyOptimization(num_ants=10, num_iterations=100, pheromone_decay=0.1, alpha=1, beta=1)
best_path, best_distance = aco.optimize(distance_matrix)
print("Best path:", best_path)
print("Best distance:", best_distance)
`current_city = visited_cities[-1]` 的意思是将`visited_cities`列表中的最后一个元素赋值给`current_city`变量。在蚁群算法中，`visited_cities`列表记录了蚂蚁已经访问的城市序列。
`[-1]` 是Python中用于索引列表的特殊语法，表示访问列表的最后一个元素。通过`visited_cities[-1]`，我们可以获取列表中最后一个访问的城市，然后将其赋值给`current_city`变量。
在蚁群算法的选择下一个城市的过程中，`current_city`表示当前蚂蚁所在的城市，根据信息素和启发式规则选择下一个要访问的城市。
就是说是获取当下的起点
`num_cities = distance_matrix.shape[0]` 的意思是获取`distance_matrix`矩阵的形状，并将其第一个维度的大小赋值给`num_cities`变量。在这种情况下，`distance_matrix`是一个二维矩阵，表示城市之间的距离或成本。
`shape`是NumPy库中的一个属性，可以用于获取数组或矩阵的形状。对于二维矩阵来说，`shape`返回一个包含两个维度大小的元组，第一个维度表示矩阵的行数，第二个维度表示矩阵的列数。
通过`distance_matrix.shape[0]`，我们可以获取矩阵的行数，也即城市的数量，然后将其赋值给`num_cities`变量。这是因为在蚁群算法中，我们需要知道要访问的城市数量，以便在算法中进行遍历和处理。
import numpy as np
import matplotlib.pyplot as plt
def visualize_ant_path(path):
# 创建一个空白图表
fig, ax = plt.subplots()
# 循环遍历路径中的每一步
for i in range(len(path) - 1):
# 当前位置和下一步的位置
current_pos = path[i]
next_pos = path[i + 1]
# 在图表中绘制线段表示蚂蚁的路径
ax.plot([current_pos[0], next_pos[0]], [current_pos[1], next_pos[1]], 'b-')
# 标记当前位置
ax.plot(current_pos[0], current_pos[1], 'ro')
# 更新图表
plt.pause(0.1)
# 最后一步的位置，绘制为绿色
ax.plot(path[-1][0], path[-1][1], 'go')
# 显示图表
plt.show()
class AntColonyOptimization:#蚂蚁类定义
def __init__(self, num_ants, num_iterations, pheromone_decay, alpha, beta):#构造函数
self.num_ants = num_ants#蚂蚁数量、列表
self.num_iterations = num_iterations#迭代次数
self.pheromone_decay = pheromone_decay#衰减系数ρ
self.alpha = alpha#弗洛蒙控制系数，全局控制系数，越大越容易形成路径依赖
self.beta = beta#图自身特点控制系数
def optimize(self, distance_matrix):
num_cities = distance_matrix.shape[0]#可选城市矩阵
self.pheromone_matrix = np.ones((num_cities, num_cities))#弗洛蒙矩阵
best_path = None
best_distance = np.inf
best_distance_progress = [] # 用于存储每次迭代后的最佳距离
for iteration in range(self.num_iterations):#迭代完，循环里每次都是一次迭代
ant_paths = self.construct_ant_paths(distance_matrix)#构建、获取每次迭代里，m只蚂蚁走的路径，就是蚂蚁群的路径矩阵
self.update_pheromone_matrix(ant_paths)#在所有蚂蚁走完后，依据其所走的路径，更新弗洛蒙矩阵，主要是加上新增的弗洛蒙浓度
current_best_path, current_best_distance = self.get_best_solution(ant_paths, distance_matrix)#获取这次迭代中所有蚂蚁走出来的最好路径总长与最好路径
if current_best_distance < best_distance:#获取更新最优
best_path = current_best_path
best_distance = current_best_distance
best_distance_progress.append(best_distance) # 将每次迭代完后的路径加入到此次迭代更新完后的最好记录里
self.pheromone_matrix = (1 - self.pheromone_decay) * self.pheromone_matrix#更新弗洛蒙矩阵，是进行挥发衰减
plt.plot(range(self.num_iterations), best_distance_progress)
plt.xlabel('Iteration')
plt.ylabel('Best Distance')
plt.title('Ant Colony Optimization Progress')
plt.show()
return best_path, best_distance#最后返回迭代完成后的最短路与最短路径
def construct_ant_paths(self, distance_matrix):
num_cities = distance_matrix.shape[0]
ant_paths = []
for ant in range(self.num_ants):#这个是让每只蚂蚁都完成一次路径，是一个循环语句，每次循环内部是对一只蚂蚁进行操作
visited_cities = []
current_city = np.random.randint(num_cities)#开始起点随机，不影响最终结果的最短
visited_cities.append(current_city)
while len(visited_cities) < num_cities:#循环，直到走完所有城市
next_city = self.select_next_city(visited_cities, distance_matrix)#依据弗洛蒙矩阵与距离矩阵与以遍历的，综合考量，随机选择下一个城市走
visited_cities.append(next_city)#加入已遍历城市，下次不再遍历
current_city = next_city#更新当前城市
ant_paths.append(visited_cities)#这个蚂蚁走完后，在本次迭代中加入它所走的路径
return ant_paths#最后返回本次迭代中所有蚂蚁走的路径
def select_next_city(self, visited_cities, distance_matrix):#每个蚂蚁在其各自起点的基础上，概率选择下一个终点
num_cities = distance_matrix.shape[0]
current_city = visited_cities[-1]#获取访问城市的最后一个元素，即此时的起点
unvisited_cities = [city for city in range(num_cities) if city not in visited_cities]
probabilities = []
for city in unvisited_cities:#遍历还没访问过的城市，获取访问这些城市的概率
pheromone = self.pheromone_matrix[current_city, city]#得到到这个城市路径上的弗洛蒙浓度
distance = distance_matrix[current_city, city]#得到到这个城市的距离
probability = pheromone**self.alpha * (1/distance)**self.beta#计算得到到这个城市的概率
probabilities.append(probability)#加入到这个城市的概率进列表里
probabilities = np.array(probabilities)
probabilities /= np.sum(probabilities)#归一化
next_city = np.random.choice(unvisited_cities, p=probabilities)#随机选择一个城市，依据概率矩阵
return next_city#返回最后选择的城市
def update_pheromone_matrix(self, ant_paths):
num_cities = self.pheromone_matrix.shape[0]
for ant_path in ant_paths:#遍历蚂蚁群的每只蚂蚁所走过的路径
for i in range(num_cities - 1):#得到这个蚂蚁路径上的城市
current_city = ant_path[i]
next_city = ant_path[i + 1]#联通这个蚂蚁所选择的路径
self.pheromone_matrix[current_city, next_city] += 1#弗洛蒙增量，增加1
def get_best_solution(self, ant_paths, distance_matrix):
best_path = None
best_distance = np.inf
for path in ant_paths:#得到蚂蚁群的每只蚂蚁走的路径
distance = self.calculate_path_distance(path, distance_matrix)#计算这只蚂蚁路径的长度
if distance < best_distance:
best_path = path
best_distance = distance
return best_path, best_distance
def calculate_path_distance(self, path, distance_matrix):
distance = 0
for i in range(len(path) - 1):
current_city = path[i]
next_city = path[i + 1]
distance += distance_matrix[current_city, next_city]
return distance
# 示例用法
distance_matrix = np.array([[0, 2, 9, 10],
[2, 0, 6, 4],
[9, 6, 0, 8],
[10, 4, 8, 0]])
aco = AntColonyOptimization(num_ants=10, num_iterations=100, pheromone_decay=0.1, alpha=1, beta=1)
best_path, best_distance = aco.optimize(distance_matrix)
visualize_ant_path(best_path)
print("Best path:", best_path)
print("Best distance:", best_distance)