算法训练|动态规划之背包问题复习

背包问题分类：（主要分为两类）

一：01背包：给一个数组或者容器，容器中的数据只能使用一次，问装满背包的最大价值为多少。

二：完全背包：给一个数组或者容器，容器中的数据可无限使用，问装满背包的最大价值为多少。

不一定是问装满背包的最大价值是多少，这只是一个通用的说法

01背包：

01背包又分为两种方法：二维数组和一维数组。（动态规划数组用dp表示，重量数组为weight，很多题目物品重量同时也是物品的价值）

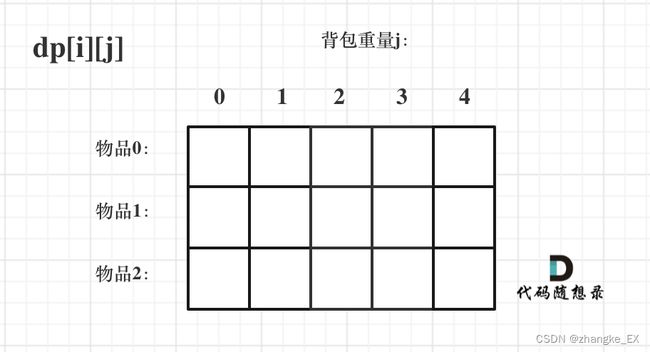
二维数组：1、dp[i][j]表示当从下标0-i的物品里面任意取，放进容量为j的背包，的最大价值。那么此时有两个方向可以推出dp[i][j]：

（1）：当不放物品i时，此时dp[i][j] = dp[i - 1][j]，即不放物品i时，背包容量为j的最大价值。

（2）：当放物品i时，此时dp[i][j] = dp[i - 1][j - weight[i]] + weight[i]，即放入物品i时，背包容量还剩j - weight[i]且此时就要从0 - i-1下标中找物品放入以及要加上i的价值。

即

dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - weight[i]] + weight[i]])

2、初始化：

（图源自代码随想录网站）

初始化一般要看情况初始化，例如当背包重量为j时则不论放什么物品都放不下所以都是0，另一方面由状态转移方程可以看出来dp[i][j]由上方以及左上方推出，所以初始化第一行和第一列即可。

3、遍历顺序：在01背包中，先遍历物品亦或是先遍历背包都是可以的。

一维数组：1、一维数组由二维数组推导而来，实质是对二维数组的压缩，

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]，即

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

（摘取自代码随想录）

2、初始化：一维数组的初始化要视情况而定且要和dp数组的定义吻合，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0。

3、遍历顺序：一维数组的遍历则只能先遍历物品再遍历背包且背包要倒序遍历，原因：若背包进行正序遍历则会导致物品被多次使用导致结果不正确，只能先遍历物品因为递推公式里，需要先得到一轮的dp[j]，那就只能让j循环在里面，要不然怎么先得到dp[j]的数据呢

---

题目例子，以下题目均是01背包在不同层面上的应用，都要分析然后回归到01问题上面来。

416. 分割等和子集 - 力扣（LeetCode）

此题分析：要使两个子集中的元素和相等，则只要求出总和再假设背包容量为总和的一半，再利用背包问题求解即可。此题中每个物品的价值即为物品的重量，设总和的一半为target，则若dp[target]  = target（dp数组含义：背包容量为target的最大价值为dp[target]）的话则满足题意要求这里即也是问能不能把背包装满若装满了则有前面等式。

1049. 最后一块石头的重量 II - 力扣（LeetCode）

此题分析：需要返回石头的最小重量，则可将数组分成两半，当两半中的元素和越接近时，最终剩下的石头重量则为最小，则此题与“分割等和子集”问题相差不大，区别在此题dp[target]不一定装满。