【算法】观光（求次短路，Dijkstra）

题目

“您的个人假期”旅行社组织了一次比荷卢经济联盟的巴士之旅。

比荷卢经济联盟有很多公交线路。

每天公共汽车都会从一座城市开往另一座城市。

沿途汽车可能会在一些城市（零或更多）停靠。

旅行社计划旅途从 S 城市出发，到 F 城市结束。

由于不同旅客的景点偏好不同，所以为了迎合更多旅客，旅行社将为客户提供多种不同线路。

游客可以选择的行进路线有所限制，要么满足所选路线总路程为 S 到 F 的最小路程，要么满足所选路线总路程仅比最小路程多一个单位长度。

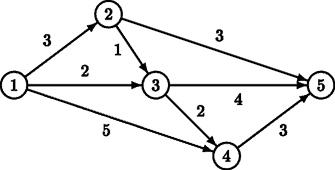
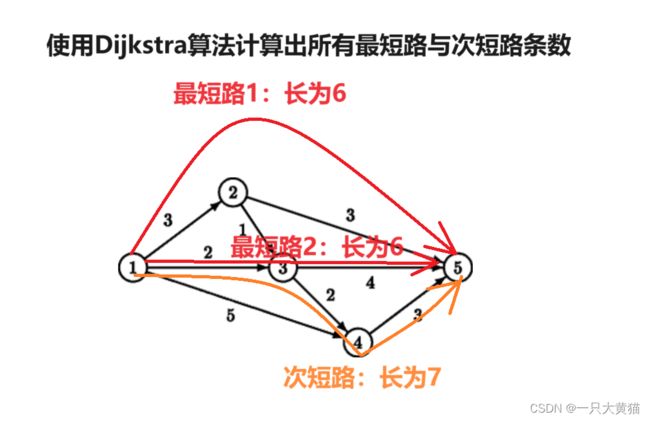
如上图所示，如果 S=1，F=5，则这里有两条最短路线 1→2→5,1→3→5，长度为 6；有一条比最短路程多一个单位长度的路线 1→3→4→5，长度为 7。

现在给定比荷卢经济联盟的公交路线图以及两个城市 S 和 F，请你求出旅行社最多可以为旅客提供多少种不同的满足限制条件的线路。

输入格式

第一行包含整数 T，表示共有 T 组测试数据。

每组数据第一行包含两个整数 N 和 M，分别表示总城市数量和道路数量。

接下来 M 行，每行包含三个整数 A,B,L，表示有一条线路从城市 A 通往城市 B，长度为 L。

需注意，线路是 单向的，存在从 A 到 B 的线路不代表一定存在从 B 到 A 的线路，另外从城市 A 到城市 B 可能存在多个不同的线路。

接下来一行，包含两个整数 S 和 F，数据保证 S 和 F 不同，并且 S、F 之间至少存在一条线路。

输出格式

每组数据输出一个结果，每个结果占一行。

数据保证结果不超过 1e9。

数据范围

2≤N≤1000
1≤M≤10000
1≤L≤1000
1≤A,B,S,F≤N

输入样例：

2
5 8
1 2 3
1 3 2
1 4 5
2 3 1
2 5 3
3 4 2
3 5 4
4 5 3
1 5
5 6
2 3 1
3 2 1
3 1 10
4 5 2
5 2 7
5 2 7
4 1

输出样例：

3
2

思路

使用Dijkstra算法保留最短路径与次短路经。 

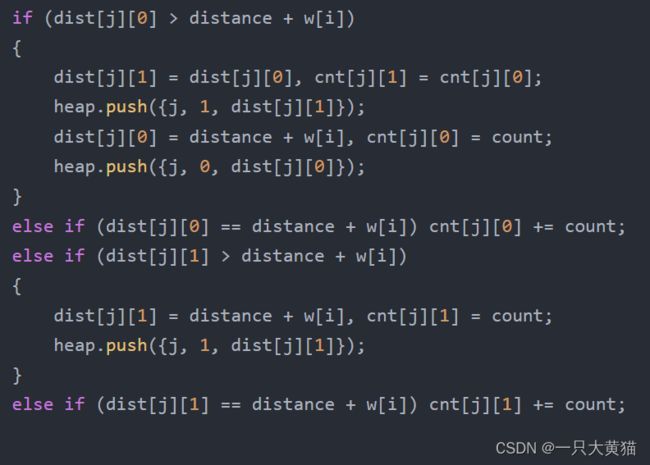
如果发现比当前最短路径还要短的路径，则当前最短路径变为次短路经。代码如下：

代码中dist[N][2]中dist[ i ][0]保留点 i 到起点的最短路径，dist[ i ][1]保留点 i 到起点的次短路径。

cnt[N][2]中cnt[ i ][0]保留点 i 到起点最短路径条数，cnt[ i ][1]保留点 i 到起点的次短路径条数。

代码

#include
using namespace std;
const int N = 1010, M = 20010;

struct Ver
{
    int id, type, dist;
    bool operator> (const Ver &W) const
    {
        return dist > W.dist;// 按照dist排序
    }
};

int n, m, S, T;
int h[N], e[M], w[M], ne[M], idx;
int dist[N][2], cnt[N][2];
bool st[N][2];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra()
{
    memset(st, 0, sizeof st);// 将st数组初始化为false
    memset(dist, 0x3f, sizeof dist);// 将dist数组初始化为正无穷
    memset(cnt, 0, sizeof cnt);// 将cnt数组初始化为0

    dist[S][0] = 0, cnt[S][0] = 1;// dist[][0]代表最小距离，dist[][1]代表次小距离
    priority_queue, greater> heap;// 建立小根堆
    heap.push({S, 0, 0});

    while (heap.size())
    {
        Ver t = heap.top();
        heap.pop();

        int ver = t.id, type = t.type, distance = t.dist, count = cnt[ver][type];
        if (st[ver][type]) continue;
        st[ver][type] = true;

        for (int i = h[ver]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dist[j][0] > distance + w[i])
            {
                dist[j][1] = dist[j][0], cnt[j][1] = cnt[j][0];
                heap.push({j, 1, dist[j][1]});
                dist[j][0] = distance + w[i], cnt[j][0] = count;
                heap.push({j, 0, dist[j][0]});
            }
            else if (dist[j][0] == distance + w[i]) cnt[j][0] += count;
            else if (dist[j][1] > distance + w[i])
            {
                dist[j][1] = distance + w[i], cnt[j][1] = count;
                heap.push({j, 1, dist[j][1]});
            }
            else if (dist[j][1] == distance + w[i]) cnt[j][1] += count;
        }
    }

    int res = cnt[T][0];
    if (dist[T][0] + 1 == dist[T][1]) res += cnt[T][1];

    return res;
}

int main()
{
    int cases;// 数据组数
    scanf("%d", &cases);
    while (cases -- )
    {
        scanf("%d%d", &n, &m);// n个点，m条边
        memset(h, -1, sizeof h);
        idx = 0;

        while (m -- )// 输入m条边
        {
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            add(a, b, c);// 建立有向边
        }
        scanf("%d%d", &S, &T);// 输入起点s，终点t

        printf("%d\n", dijkstra());// 输出答案
    }

    return 0;
}

难度：中等

时/空限制：1s / 64MB

来源：《算法竞赛进阶指南》

算法标签 图论最短路单源次短路及其条数

题目来自：383. 观光 - AcWing题库