m基于CNN卷积神经网络的IBDFE单载波频域均衡算法

1.算法描述

   单载波频域均衡(SC-FDE)是解决符号间干扰(ISI)问题的一项重要技术。相比于单载波时域均衡(SC-TDE)技术和正交频分复用(OFDM)技术,SC-FDE技术具有复杂度低、峰均功率比小的优点。但是,SC-FDE技术中,均衡算法的性能与复杂度存在制约关系,传统均衡算法无法在二者之间取得较好的折衷。       



   在单载波频域均衡系统中，线性均衡算法虽然简单易行，但是其抑制噪声干扰和符号间干扰的能力有限，因此需要引入非线性的反馈和迭代机制以进一步提升系统性能。迭代块判决反馈均衡（Iterative Block Decision Feed-back Equalization ，IBDFE）就是一种行之有效的非线性算法，但其缺点是计算复杂度高。传统的IBDFE算法结构如下：

   从结构可知，IBDFE由前馈滤波器和反馈滤波器构成，其中C和B表示前馈滤波器和反馈滤波器的系数。从现有的文献和资料上看，目前该结构在计算过程中，每一次迭代均需要进行系数的估计，从而增加了系统实现复杂度。针对问题，目前主要的研究成果例如LC-IBDFE等，其通过将判决信号中的误差与期望信号分离，从而降低了复杂度。但是类似LC-IBDFE的改进思路，其是基于每次迭代的误比特率相同且很小的假设的，实际中这种情况很难满足条件。另外就是在IBDFE中，出现信道严重衰落的时候，会导致过高的相关因子的估计，从而导致误差的扩散。针对这个问题，现有成果主要有联合信道估计和信道均衡的联合均衡算法。但是这样算法的复杂度又进一步增加。     



  我们这里做一个简单的改进：

    将CNN训练后的网络权值Wcnn和信道H相乘，将相乘后的结果用于BK的更新和补偿。由于Bk和Wk是相关的，所以这里直接将CNN用于控制WK即可。从而获得最后的结果。



    在单载波频域均衡系统中，线性均衡算法虽然简单易行，但是其抑制噪声干扰和符号间干扰的能力有限，因此需要引入非线性的反馈和迭代机制以进一步提升系统性能。迭代块判决反馈均衡（Iterative Block Decision Feed-back Equalization ，IBDFE）就是一种行之有效的非线性算法，但其缺点是计算复杂度高。



   卷积神经网络默认输入是图像，可以让我们把特定的性质编码入网络结构，使是我们的前馈函数更加有效率，并减少了大量参数。卷积神经网络是一种带有卷积结构的深度神经网络，卷积结构可以减少深层网络占用的内存量，其三个关键的操作，其一是局部感受野，其二是权值共享，其三是pooling层，有效的减少了网络的参数个数，缓解了模型的过拟合问题。



   卷积神经网络是一种多层的监督学习神经网络，隐含层的卷积层和池采样层是实现卷积神经网络特征提取功能的核心模块。该网络模型通过采用梯度下降法最小化损失函数对网络中的权重参数逐层反向调节，通过频繁的迭代训练提高网络的精度。卷积神经网络的低隐层是由卷积层和最大池采样层交替组成，高层是全连接层对应传统多层感知器的隐含层和逻辑回归分类器。第一个全连接层的输入是由卷积层和子采样层进行特征提取得到的特征图像。最后一层输出层是一个分类器，可以采用逻辑回归，Softmax回归甚至是支持向量机对输入图像进行分类。

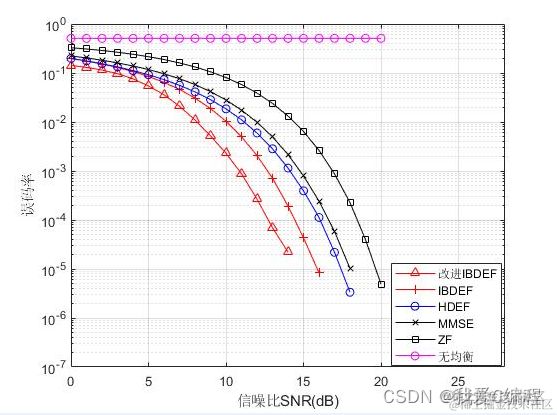
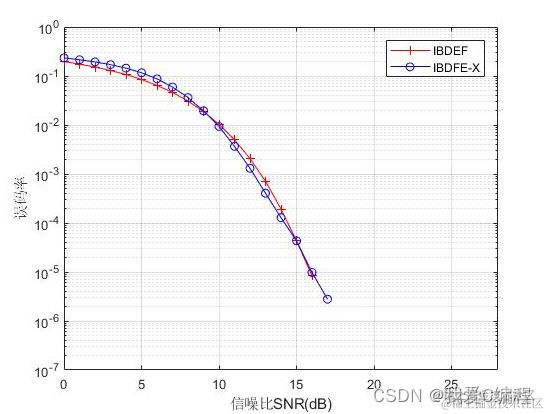
2.仿真效果预览

matlab2022a仿真结果如下：

3.MATLAB核心程序

`%信道模型`

`Channel  = rayleighchan(Ts,Fd,tau,pdb);`

`%FFT变换`

`H_channel0 = ``fft``(Channel.PathGains./``sqrt``(``sum``((``abs``(Channel.PathGains)).^2)),Blk_size+Chu_size+Chu_size);`

` ` 

`%CHU序列`

`Chuseq = ``zeros``(1,Chu_size);`

`for` `k = 0:Chu_size-1`

`    ``tmps(k+1) = ``pi``*k^2./Chu_size;`

`end`

`I      = ``cos``(tmps);`

`Q      = ``sin``(tmps);`

`Chuseq = I+``sqrt``(-1)*Q;`

`%误码率`

`%turbo参数`

`Mss    = 295;`

`for` `n = 1:``length``(SNR)`

`    ``ErrMMSE = 0;`

`    ``for` `k = 1:NFrame`

`        ``[n,k]`

`        ``rng(k);`

`        ``%随机`

`        ``Tdin       = ``rand``(1,Mss)>0.5;`

`        ``%利用turbo的交织器，构建TB-DEF,三路输出`

`        ``output     = [func_turbo_code(Tdin)];`

`        ``output     = ``reshape``(output, 1, []);`

`        ``seridata1  = [output,0,0];`

`        ` 

`        ``%调制`

`        ``Data       = modulation(seridata1,Modsel);`

`        ``Tx         = [Chuseq,Data,Chuseq];`

`        ``Channel0   = Channel.PathGains./``sqrt``(``sum``((``abs``(Channel.PathGains)).^2));`

`        ``Rx1        = ``filter``(Channel0,1,Tx);          `

`        ``Rx2        = awgn(Rx1,SNR(n),``'measured'``);`

`        ``Rx3        = Rx2;``%(Chu_size+1:Chu_size+Blk_size);  `

`        ``H_channel  = H_channel0;    `

`        ``%频域均衡`

`        ``Y          = ``fft``(Rx3,Blk_size+Chu_size+Chu_size);      `

`        ``Wk         = ``conj``(H_channel)./(H_channel.*``conj``(H_channel)+10^(-SNR(n)/10));`

`        ``Zk         = Y.*Wk;`

`        ``Qk         = ``zeros``(``size``(Zk));`

`        ``Bk         = (Blk_size-Chu_size)*(``abs``(H_channel).^2+10^(-SNR(n)/10))./(``sum``(``abs``(H_channel).^2+10^(-SNR(n)/10)))-1;`

`        ``P          = 5;`

`        ``%调用CNN神经网络的输出权值`

`        ``load` `CNNmodel.mat`

`        ``Iter       = 5;`

`        ``for` `iter = 1:Iter`

`            ``Wk = ``conj``(H_channel)./(H_channel.*``conj``(H_channel)+10^(-SNR(n)/10)/P).*(1+Bk); `

`            ``Zk         = Y.*Wk;`

`            ``Uk         = Zk-Qk;`

`            ``RxMMSE0    = ``ifft``(Uk,Blk_size+Chu_size+Chu_size);   `

`            ``xn         = ``sign``(``real``(RxMMSE0))+``sqrt``(-1)*``sign``(``imag``(RxMMSE0));`

`            ``%去UW`

`            ``RxMMSE1    = xn(Chu_size+1:Blk_size);`

`            ``%进行判决`

`            ``RxMMSE     = demodulation(RxMMSE1,Modsel);  `

`            ``Tdecode    = ``round``(func_turbo_decode(2*RxMMSE(1:``end``-2)-1));`

`            ``tmps       = Tdecode;`

`            ` 

`            ``XK         = ``fft``([tmps,Chuseq],``length``(RxMMSE1));`

`            ``%调用CNN深度学习神经网络，计算Bk值`

`            ``Bk0        =([H_channel.*``conj``(H_channel)]+10^(-SNR(n)/10)/P)/(``mean``(([H_channel.*``conj``(H_channel)]+10^(-SNR(n)/10)/P)))/(Blk_size)-1;`

`            ``Bk         = func_CNN(H_channel,Bk0,cnn);`

`            ``Qk         = [XK,``ones``(1,192)].*Bk;`

`        ``end`

`        ``CrrMMSE    = ``find``((Tdin-Tdecode) == 0);`

`        ``ErrMMSE    = ErrMMSE+(Mss-``length``(CrrMMSE));`

`    ``end`

`    ``%统计误码率`

`    ``errors(n) = ErrMMSE/(Mss*NFrame*Modsel);`

`end`

最后

为了帮助大家更好的学习人工智能，这里给大家准备了一份人工智能入门/进阶学习资料，里面的内容都是适合学习的笔记和资料，不懂编程也能听懂、看懂，所有资料朋友们如果有需要全套人工智能入门+进阶学习资源包，可以在评论区或扫.码领取哦）~

在线教程

• 麻省理工学院人工智能视频教程 – 麻省理工人工智能课程
• 人工智能入门 – 人工智能基础学习。Peter Norvig举办的课程
• EdX 人工智能 – 此课程讲授人工智能计算机系统设计的基本概念和技术。
• 人工智能中的计划 – 计划是人工智能系统的基础部分之一。在这个课程中，你将会学习到让机器人执行一系列动作所需要的基本算法。
• 机器人人工智能 – 这个课程将会教授你实现人工智能的基本方法，包括：概率推算，计划和搜索，本地化，跟踪和控制，全部都是围绕有关机器人设计。
• 机器学习 – 有指导和无指导情况下的基本机器学习算法
• 机器学习中的神经网络 – 智能神经网络上的算法和实践经验
• 斯坦福统计学习

有需要的小伙伴，可以点击下方链接免费领取或者V扫描下方二维码免费领取
​

人工智能书籍

• OpenCV（中文版）.(布拉德斯基等)
• OpenCV+3计算机视觉++Python语言实现+第二版
• OpenCV3编程入门 毛星云编著
• 数字图像处理_第三版
• 人工智能:一种现代的方法
• 深度学习面试宝典
• 深度学习之PyTorch物体检测实战
• 吴恩达DeepLearning.ai中文版笔记
• 计算机视觉中的多视图几何
• PyTorch-官方推荐教程-英文版
• 《神经网络与深度学习》(邱锡鹏-20191121)
• …
  
  有需要的小伙伴，可以点击下方链接免费领取或者V扫描下方二维码免费领取
  ​

第一阶段：零基础入门（3-6个月）

新手应首先通过少而精的学习，看到全景图，建立大局观。 通过完成小实验，建立信心，才能避免“从入门到放弃”的尴尬。因此，第一阶段只推荐4本最必要的书（而且这些书到了第二、三阶段也能继续用），入门以后，在后续学习中再“哪里不会补哪里”即可。

第二阶段：基础进阶（3-6个月）

熟读《机器学习算法的数学解析与Python实现》并动手实践后，你已经对机器学习有了基本的了解，不再是小白了。这时可以开始触类旁通，学习热门技术，加强实践水平。在深入学习的同时，也可以探索自己感兴趣的方向，为求职面试打好基础。

第三阶段：工作应用

这一阶段你已经不再需要引导，只需要一些推荐书目。如果你从入门时就确认了未来的工作方向，可以在第二阶段就提前阅读相关入门书籍（对应“商业落地五大方向”中的前两本），然后再“哪里不会补哪里”。

有需要的小伙伴，可以点击下方链接免费领取或者V扫描下方二维码免费领取
​