ID3决策树算法及其Python实现

一、决策树算法

决策树是一种基于树结构来进行决策的分类算法，我们希望从给定的训练数据集学得一个模型（即决策树），用该模型对新样本分类。决策树可以非常直观展现分类的过程和结果，一旦模型构建成功，对新样本的分类效率也相当高。
最经典的决策树算法有ID3、C4.5、CART，其中ID3算法是最早被提出的，它可以处理离散属性样本的分类，C4.5和CART算法则可以处理更加复杂的分类问题，本文重点介绍ID3算法。

基础理论

1. 纯度（purity）
   对于一个分支结点，如果该结点所包含的样本都属于同一类，那么它的纯度为1，而我们总是希望纯度越高越好，也就是尽可能多的样本属于同一类别。那么如何衡量“纯度”呢？由此引入“信息熵”的概念。

2. 信息熵（information entropy）
   假定当前样本集合D中第k类样本所占的比例为pk（k=1,2,…,|y|），则D的信息熵定义为：
   Ent(D) = -∑k=1 pk·log2 pk（约定若p=0，则log2 p=0）
   显然，Ent(D)值越小，D的纯度越高。因为0<=pk<= 1,故log2 pk<=0，Ent(D)>=0. 极限情况下，考虑D中样本同属于同一类，则此时的Ent(D)值为0（取到最小值）。当D中样本都分别属于不同类别时，Ent(D)取到最大值log2 |y|.

3. 信息增益（information gain）
   假定离散属性a有V个可能的取值{a1,a2,…,aV}. 若使用a对样本集D进行分类，则会产生V个分支结点，记Dv为第v个分支结点包含的D中所有在属性a上取值为av的样本。不同分支结点样本数不同，我们给予分支结点不同的权重：|Dv|/|D|, 该权重赋予样本数较多的分支结点更大的影响、由此，用属性a对样本集D进行划分所获得的信息增益定义为：

   Gain(D,a) = Ent(D)-∑v=1 |Dv|/|D|·Ent(Dv)

其中，Ent(D)是数据集D划分前的信息熵，∑v=1 |Dv|/|D|·Ent(Dv)可以表示为划分后的信息熵。“前-后”的结果表明了本次划分所获得的信息熵减少量，也就是纯度的提升度。显然，Gain(D,a) 越大，获得的纯度提升越大，此次划分的效果越好。

4. 增益率(gain ratio)
   基于信息增益的最优属性划分原则——信息增益准则，对可取值数据较多的属性有所偏好。C4.5算法使用增益率替代信息增益来选择最优划分属性，增益率定义为：

   Gain_ratio(D,a) = Gain(D,a)/IV(a)

其中

          IV(a) = -∑v=1 |Dv|/|D|·log2 |Dv|/|D|

称为属性a的固有值。属性a的可能取值数目越多（即V越大），则IV(a)的值通常会越大。这在一定程度上消除了对可取值数据较多的属性的偏好。

事实上，增益率准则对可取值数目较少的属性有所偏好，C4.5算法并不是直接使用增益率准则，而是先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

5. 基尼指数(Gini index)
   CART决策树算法使用基尼指数来选择划分属性，基尼指数定义为：

          Gini(D) = ∑k=1 ∑k'≠1 pk·pk' = 1- ∑k=1  pk·pk
   

   可以这样理解基尼指数：从数据集D中随机抽取两个样本，其类别标记不一致的概率。Gini(D)越小，纯度越高。

   属性a的基尼指数定义：

         Gain_index(D,a) = ∑v=1 |Dv|/|D|·Gini(Dv)
   

   使用基尼指数选择最优划分属性，即选择使得划分后基尼指数最小的属性作为最优划分属性。

决策树的学习过程

一棵决策树的生成过程主要分为以下3个部分:

特征选择：特征选择是指从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准，如何选择特征有着很多不同量化评估标准标准，从而衍生出不同的决策树算法。

决策树生成： 根据选择的特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止生长。 树结构来说，递归结构是最容易理解的方式。

剪枝：决策树容易过拟合，一般来需要剪枝，缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。

在讲解特征选择前，我们先了解一些概念。

决策树节点的不纯度（impurity）

ID3算法

ID3算法是最早提出的一种决策树算法，ID3算法的核心是在决策树各个节点上应用信息增益准则来选择特征，递归的构建决策树。具体方法是：从根节点开始，对节点计算所有可能的特征的信息增益，选择信息增益最大的特征作为节点的特征，由该特征的不同取值建立子节点：再对子节点递归的调用以上方法，构建决策树：直到所有的特征信息增益均很小或没有特征可以选择为止。
决策树是根据信息增益来进行特征选择的，信息增益定义为

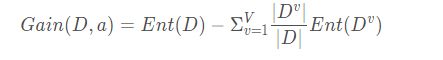
其中D为总的样本，a为属性，v为在属性a中的v类样本，信息增益越大，表明该属性对分类的相关性越大。Ent()表示信息熵（entropy），公式如下：

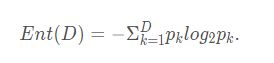
k表示在样本D中的第k类样本，pk表示第k类样本所占样本总体的概率。类比于现实中的熵，可以理解为，信息熵越小，表明纯度越高。

二、实现针对西瓜数据集的ID3算法

watermalon.txt文件

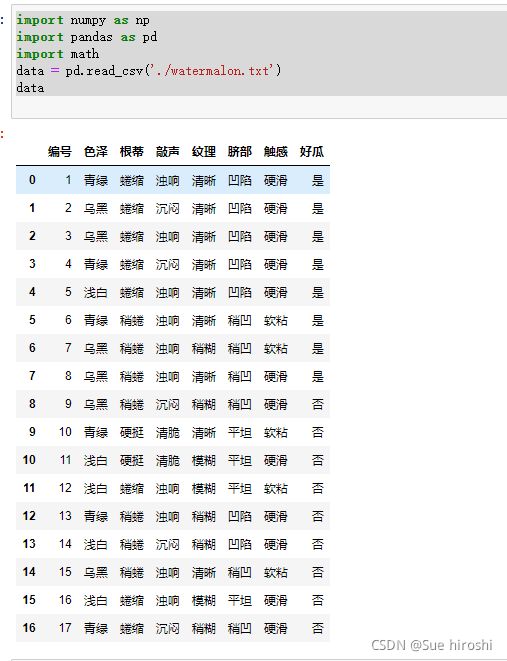
实现代码

import numpy as np
import pandas as pd
import math
data = pd.read_csv('./watermalon.txt')
data

def info(x,y):
    if x != y and x != 0:
        # 计算当前情况的熵
        return -(x/y)*math.log2(x/y) - ((y-x)/y)*math.log2((y-x)/y)
    if x == y or x == 0:
        # 纯度最大，熵值为0
        return 0
        info_D = info(8,17)
        info_D

# 计算每种情况的熵
seze_black_entropy = -(4/6)*math.log2(4/6)-(2/6)*math.log2(2/6)
seze_green_entropy = -(3/6)*math.log2(3/6)*2
seze_white_entropy = -(1/5)*math.log2(1/5)-(4/5)*math.log2(4/5)

# 计算色泽特征色信息熵
seze_entropy = (6/17)*seze_black_entropy+(6/17)*seze_green_entropy+(5/17)*seze_white_entropy
print(seze_entropy)
# 计算信息增益
info_D - seze_entropy

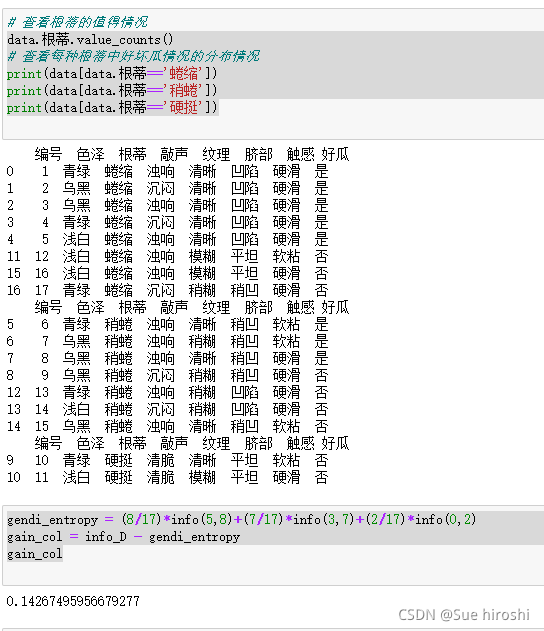
data.根蒂.value_counts()
# 查看每种根蒂中好坏瓜情况的分布情况
print(data[data.根蒂=='蜷缩'])
print(data[data.根蒂=='稍蜷'])
print(data[data.根蒂=='硬挺'])

gendi_entropy = (8/17)*info(5,8)+(7/17)*info(3,7)+(2/17)*info(0,2)
gain_col = info_D - gendi_entropy
gain_col

data.敲声.value_counts()
# 查看每种敲声中好坏瓜情况的分布情况
print(data[data.敲声=='浊响'])
print(data[data.敲声=='沉闷'])
print(data[data.敲声=='清脆'])
qiaosheng_entropy = (10/17)*info(6,10)+(5/17)*info(2,5)+(2/17)*info(0,2)
info_gain = info_D - qiaosheng_entropy
info_gain

data.纹理.value_counts()
# 查看每种纹理中好坏瓜情况的分布情况
print(data[data.纹理=="清晰"])
print(data[data.纹理=="稍糊"])
print(data[data.纹理=="模糊"])
wenli_entropy = (9/17)*info(7,9)+(5/17)*info(1,5)+(3/17)*info(0,3)
info_gain = info_D - wenli_entropy
info_gain

data.脐部.value_counts()
# 查看每种脐部中好坏瓜情况的分布情况
print(data[data.脐部=="凹陷"])
print(data[data.脐部=="稍凹"])
print(data[data.脐部=="平坦"])
qidai_entropy = (7/17)*info(5,7)