机器学习-白板推导系列(六)(2) - 约束优化问题
6. 约束优化问题
6.1 弱对偶性证明
6.1.1 概述
- 约束优化问题
约束优化问题的 原 问 题 ( P r i m a l P r o b l e m ) \color{red}原问题(Primal Problem) 原问题(PrimalProblem)的一般形式如下:
{ m i n x f ( x ) , x ∈ R p s . t . m i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , M s . t . n j ( x ) = 0 , j = 1 , 2 , ⋯ , N (6.1.1) \left\{\begin{matrix} \underset{x}{min}\; f(x),x\in \mathbb{R}^{p}\\ s.t.\; m_{i}(x)\leq 0,i=1,2,\cdots ,M\\ s.t.\; n_{j}(x)=0,j=1,2,\cdots ,N \end{matrix}\right.\tag{6.1.1} ⎩⎨⎧xminf(x),x∈Rps.t.mi(x)≤0,i=1,2,⋯,Ms.t.nj(x)=0,j=1,2,⋯,N(6.1.1)
求解约束优化问题需要用到拉格朗日乘子法,定义拉格朗日函数:
L ( x , λ , η ) = f ( x ) + ∑ i = 1 M λ i m i ( x ) + ∑ j = 1 N η j n j ( x ) (6.1.2) L(x,\lambda ,\eta )=f(x)+\sum_{i=1}^{M}\lambda _{i}m_{i}(x)+\sum_{j=1}^{N}\eta _{j}n_{j}(x)\tag{6.1.2} L(x,λ,η)=f(x)+i=1∑Mλimi(x)+j=1∑Nηjnj(x)(6.1.2)
其中 λ , η \lambda ,\eta λ,η分别是 M 维 M维 M维、 N 维 N维 N维向量。 - 无约束优化问题
把原问题转化为无优化问题,这两个优化问题具有同样的解:
{ m i n x m a x λ , η L ( x , λ , η ) s . t . λ i ≥ 0 (6.1.3) \color{red}\left\{\begin{matrix} \underset{x}{min}\; \underset{\lambda ,\eta }{max}\; L(x,\lambda ,\eta )\\ s.t.\; \lambda _{i}\geq 0 \end{matrix}\right.\tag{6.1.3} {xminλ,ηmaxL(x,λ,η)s.t.λi≥0(6.1.3)证明:以不等式约束为例
- 如果 x x x违反了约束 m i ( x ) ≤ 0 m_{i}(x)\leq 0 mi(x)≤0,即 m i ( x ) > 0 m_{i}(x)>0 mi(x)>0,由于 λ i ≥ 0 \lambda _{i}\geq 0 λi≥0, m a x λ L = ∞ \underset{\lambda }{max}\; L=\infty λmaxL=∞。
- 如果 x x x符合约束 m i ( x ) ≤ 0 m_{i}(x)\leq 0 mi(x)≤0,由于 λ i ≥ 0 \lambda _{i}\geq 0 λi≥0, m a x λ L ≠ ∞ ( 此 时 λ i = 0 ) \underset{\lambda }{max}\; L\neq \infty (此时\lambda _{i}=0) λmaxL=∞(此时λi=0).
因此 m i n x m a x λ L = m i n x { m a x λ L ⏟ x 符 合 约 束 , ∞ ⏟ x 不 符 合 约 束 } \underset{x}{min}\; \underset{\lambda }{max}\; L=\underset{x}{min}\left \{\underset{x符合约束}{\underbrace{\underset{\lambda }{max}\; L}},\underset{x不符合约束}{\underbrace{\infty }}\right \} xminλmaxL=xmin⎩⎪⎪⎨⎪⎪⎧x符合约束 λmaxL,x不符合约束 ∞⎭⎪⎪⎬⎪⎪⎫
6.1.2 对偶问题
- 对偶问题
公式(6.1.3)原问题的对偶问题为
{ m a x λ , η m i n x L ( x , λ , η ) s . t . λ i ≥ 0 (6.1.4) \color{red}\left\{\begin{matrix} \underset{\lambda ,\eta }{max}\; \underset{x}{min}\;L(x,\lambda ,\eta )\\ s.t.\; \lambda _{i}\geq 0 \end{matrix}\right.\tag{6.1.4} {λ,ηmaxxminL(x,λ,η)s.t.λi≥0(6.1.4)
可以看到 原 问 题 是 关 于 x 的 函 数 , 对 偶 问 题 是 关 于 λ , η 的 函 数 \color{blue}原问题是关于x的函数,对偶问题是关于\lambda ,\eta的函数 原问题是关于x的函数,对偶问题是关于λ,η的函数。 - 弱对偶问题
弱对偶问题有如下定理:
m a x λ , η m i n x L ( x , λ , η ) ≤ m i n x m a x λ , η L ( x , λ , η ) (6.1.5) \color{red}\underset{\lambda ,\eta }{max}\; \underset{x}{min}\;L(x,\lambda ,\eta )\leq \underset{x}{min}\;\underset{\lambda ,\eta }{max}\;L(x,\lambda ,\eta )\tag{6.1.5} λ,ηmaxxminL(x,λ,η)≤xminλ,ηmaxL(x,λ,η)(6.1.5)
弱对偶性可以理解为: 对 偶 问 题 ≤ 原 问 题 \color{blue}对偶问题 \leq 原问题 对偶问题≤原问题。我们假设:令 对 偶 问 题 ( d u a l ) 为 d , 原 问 题 ( p r i m a l ) 为 p \color{blue}对偶问题(dual)为d,原问题(primal)为p 对偶问题(dual)为d,原问题(primal)为p;则我们要证明: d ≤ p \color{blue}d\le p d≤p,即: m a x λ , η m i n x L ( x , λ , η ) ≤ m i n x m a x λ , η L ( x , λ , η ) \color{blue}\underset{\lambda,\eta}{max}\ \underset{x}{min} \ L(x, \lambda,\eta) \le \underset{x}{min} \ \underset{\lambda,\eta}{max} \ L(x, \lambda,\eta) λ,ηmax xmin L(x,λ,η)≤xmin λ,ηmax L(x,λ,η)
可以从机器学习-白板推导系列(六)(1)中:凤头和鸡头的角度理解,也可以从以下证明理解:
证明:- L ( x , λ , η ) ≤ m a x λ , η L ( x , λ , η ) L(x, \lambda,\eta) \le\underset{\lambda,\eta}{max} \ L(x, \lambda,\eta) L(x,λ,η)≤λ,ηmax L(x,λ,η)(原来的肯定小于最大的);
- m i n x L ( x , λ , η ) ≤ L ( x , λ , η ) \underset{x}{min} \ L(x, \lambda,\eta) \le \ L(x, \lambda,\eta) xmin L(x,λ,η)≤ L(x,λ,η)(最小的肯定小于原来的);
- 因此 m i n x L ( x , λ , η ) ≤ L ( x , λ , η ) ≤ m a x λ , η L ( x , λ , η ) \underset{x}{min} \ L(x, \lambda,\eta) \le \ L(x, \lambda,\eta) \le\underset{\lambda,\eta}{max} \ L(x, \lambda,\eta) xmin L(x,λ,η)≤ L(x,λ,η)≤λ,ηmax L(x,λ,η);
- 则可写出:
m i n x L ( x , λ , η ) ⏟ A ( λ , η ) ≤ L ( x , λ , η ) ≤ m a x λ , η L ( x , λ , η ) ⏟ B ( x ) ⇒ A ( λ , η ) ≤ B ( x ) ⇒ A ( λ , η ) ≤ m i n B ( x ) ⇒ m a x A ( λ , η ) ≤ m i n B ( x ) ⇒ m a x λ , η m i n x L ( x , λ , η ) ≤ L ( x , λ , η ) ≤ m i n x m a x λ , η L ( x , λ , η ) \underset{A(\lambda ,\eta )}{\underbrace{\underset{x}{min}\;L(x,\lambda ,\eta )}}\leq L(x,\lambda ,\eta )\leq \underset{B(x)}{ \underbrace{\underset{\lambda ,\eta }{max}L(x,\lambda ,\eta )}}\\ \Rightarrow A(\lambda ,\eta )\leq B(x)\\ \Rightarrow A(\lambda ,\eta )\leq min\; B(x)\\ \Rightarrow max\; A(\lambda ,\eta )\leq min\; B(x)\\ \Rightarrow \underset{\lambda ,\eta }{max}\;\underset{x}{min}\;L(x,\lambda ,\eta )\leq L(x,\lambda ,\eta )\leq \underset{x}{min}\;\underset{\lambda ,\eta }{max}\; L(x,\lambda ,\eta ) A(λ,η) xminL(x,λ,η)≤L(x,λ,η)≤B(x) λ,ηmaxL(x,λ,η)⇒A(λ,η)≤B(x)⇒A(λ,η)≤minB(x)⇒maxA(λ,η)≤minB(x)⇒λ,ηmaxxminL(x,λ,η)≤L(x,λ,η)≤xminλ,ηmaxL(x,λ,η)
6.2 对偶关系的几何解释
6.2.1 概述
- 问题概述
假设约束优化问题是:
{ m i n x f ( x ) , x ∈ R p s . t . m ( x ) ≤ 0 (6.2.1) \left\{\begin{matrix} \underset{x}{min}\; f(x),x\in \mathbb{R}^{p}\\ s.t.\; m(x)\leq 0 \end{matrix}\right.\tag{6.2.1} {xminf(x),x∈Rps.t.m(x)≤0(6.2.1)
其 定 义 域 D 定义域D 定义域D为 d o m f ∩ d o m m (6.2.2) dom\; f\cap dom\; m\tag{6.2.2} domf∩domm(6.2.2)
对于上述约束优化问题,可以写出它的拉格朗日函数:
L ( x , λ ) = f ( x ) + λ m ( x ) , λ ≥ 0 L(x,\lambda )=f(x)+\lambda m(x),\lambda \geq 0 L(x,λ)=f(x)+λm(x),λ≥0
其对偶问题为: max λ min x L ( x , λ ) (6.2.3) \underset {\lambda}{\max} \underset {x}{\min} \ L(x, \lambda)\tag{6.2.3} λmaxxmin L(x,λ)(6.2.3) - 问题简化
- 令 p ∗ p^* p∗ 为原问题: p ∗ = m i n f ( x ) p^{*}=min\; f(x) p∗=minf(x)
- 令 d ∗ d^* d∗ 为对偶问题: d ∗ = m a x λ m i n x L ( x , λ ) d^{*}=\underset{\lambda }{max}\; \underset{x}{min}\; L(x,\lambda ) d∗=λmaxxminL(x,λ)
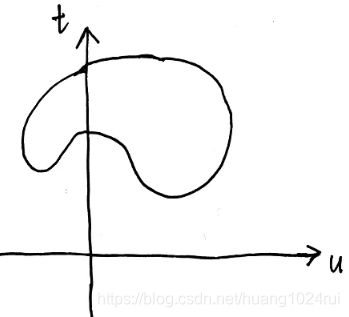
- 定义集合 G G G: G = { ( m ( x ) , f ( x ) ) ∣ x ∈ D } = { ( u , t ) ∣ x ∈ D } (6.2.4) G=\left \{(m(x),f(x))|x\in D\right \}\\ =\left \{(u,t)|x\in D\right \}\tag{6.2.4} G={(m(x),f(x))∣x∈D}={(u,t)∣x∈D}(6.2.4)
集合G在二维坐标系下表示的空间假设为下图:
6.2.2 对偶关系
- 将 p ∗ p^* p∗和 d ∗ d^* d∗ 用集合表示
- 令 i n f inf inf表示求集合的下确界,则
p ∗ = min f ( x ) = min t = inf { t ∣ ( u , t ) ∈ G , u ≤ 0 } (6.2.5) \color{blue}p^*=\min f(x) = \min t=\inf\{t|(u,t)\in G, u\le 0\}\tag{6.2.5} p∗=minf(x)=mint=inf{t∣(u,t)∈G,u≤0}(6.2.5)
d ∗ = max λ min x L ( x , λ ) = max λ min x ( t + λ u ) = max λ inf { t + λ u ∣ ( u , t ) ∈ G } d^* = \underset {\lambda}{\max} \underset {x}{\min} \ L(x, \lambda) =\underset {\lambda}{\max} \underset {x}{\min}\ (t+\lambda u) =\underset {\lambda}{\max} \ \inf \{ t+\lambda u|(u,t)\in G\} d∗=λmaxxmin L(x,λ)=λmaxxmin (t+λu)=λmax inf{t+λu∣(u,t)∈G}
令 g ( λ ) = inf { t + λ u ∣ ( u , t ) ∈ G } g(\lambda)=\inf \{ t+\lambda u|(u,t)\in G\} g(λ)=inf{t+λu∣(u,t)∈G},因此:
d ∗ = max λ g ( λ ) (6.2.6) \color{blue}d^*=\underset {\lambda}{\max} \ g(\lambda)\tag{6.2.6} d∗=λmax g(λ)(6.2.6)
- 令 i n f inf inf表示求集合的下确界,则
- 弱对偶关系证明
将 p ∗ p^* p∗和 d ∗ d^* d∗ 用几何表示- p ∗ p^* p∗在图中可以表示为:
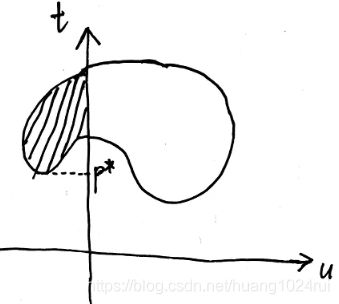
- d ∗ d^* d∗的表示
t + λ u = b t+\lambda u=b t+λu=b表示以 − λ ( λ ≥ 0 ) -\lambda(\lambda\ \ge 0) −λ(λ ≥0)为斜率, 以 b b b为截距的直线,则: - 因此从图中可以看出 p ∗ > d ∗ p^*>d^* p∗>d∗:
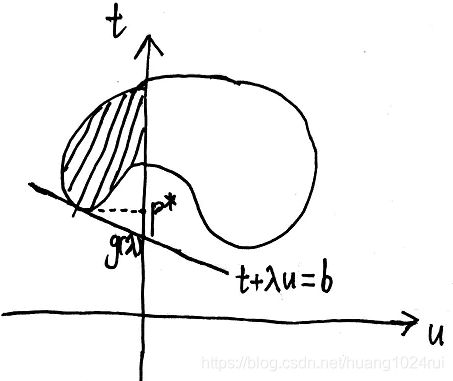
则弱对偶关系 p ∗ > d ∗ p^*>d^* p∗>d∗证毕: m a x λ , η m i n x L ( x , λ , η ) < m i n x m a x λ , η L ( x , λ , η ) (6.2.7) \color{red}\underset{\lambda ,\eta }{max}\; \underset{x}{min}\;L(x,\lambda ,\eta )< \underset{x}{min}\;\underset{\lambda ,\eta }{max}\;L(x,\lambda ,\eta )\tag{6.2.7} λ,ηmaxxminL(x,λ,η)<xminλ,ηmaxL(x,λ,η)(6.2.7)
- p ∗ p^* p∗在图中可以表示为:
- 强对偶关系
在某些特殊情况下可以使得强对偶关系成立,在图中表示如下:

如果一个约束优化问题是凸优化问题且同时满足Slater条件,那么可以使得 d ∗ = p ∗ d^*=p^* d∗=p∗:
凸 优 化 + S l a t e r 条 件 ⇒ ( d ∗ = p ∗ ) \color{red}凸优化+Slater条件\Rightarrow (d^*=p^*) 凸优化+Slater条件⇒(d∗=p∗)
- 但是 d ∗ = p ∗ d^*=p^* d∗=p∗并不能推出该约束优化问题是凸优化问题且同时满足Slater条件,这是因为Slater条件是 d ∗ = p ∗ d^*=p^* d∗=p∗的充分不必要条件,还有其他的条件可以使得约束优化问题满足 d ∗ = p ∗ d^*=p^* d∗=p∗。
- SVM是一个二次规划问题,其天生满足强对偶关系。
6.3 对偶关系之Slater Condition的解释
- Slater条件
{ ∃ x ^ ∈ r e l i n t D s . t . m i ( x ) < 0 ; ∀ i = 1 , ⋯ , M (6.3.1) \begin{cases} \exists \hat x \in relint \ D\\ s.t. \ \ m_i(x)<0;\; \forall i=1,\cdots,M\end{cases}\tag{6.3.1} {∃x^∈relint Ds.t. mi(x)<0;∀i=1,⋯,M(6.3.1)relint是指域内,不包括边界。
- Slater条件说明
有以下两点说明:- 对于大多数凸优化问题,Slater条件是成立的;
- 放松的Slater条件:对于约束条件,如果有 k k k 个 m i ( x ) m_{i}(x) mi(x)是仿射函数,那么只需要验证其他 M − k M-k M−k个条件即可。因为在定义域内寻找一个满足所有 m i ( x ) < 0 m_{i}(x)<0 mi(x)<0的点是比较困难的,因此 放 松 的 S l a t e r 条 件 放松的Slater条件 放松的Slater条件会减少一些复杂度。
SVM中的问题,是凸二次优化,其约束条件是仿射函数,所以天然符合放松的slater条件。
6.4 对偶关系之KKT条件
6.4.1 概述
- 原问题
原问题为:
{ m i n x f ( x ) , x ∈ R p s . t . m i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , M s . t . n j ( x ) = 0 , j = 1 , 2 , ⋯ , N (6.4.1) \left\{\begin{matrix} \underset{x}{min}\; f(x),x\in \mathbb{R}^{p}\\ s.t.\; m_{i}(x)\leq 0,i=1,2,\cdots ,M\\ s.t.\; n_{j}(x)=0,j=1,2,\cdots ,N \end{matrix}\right.\tag{6.4.1} ⎩⎨⎧xminf(x),x∈Rps.t.mi(x)≤0,i=1,2,⋯,Ms.t.nj(x)=0,j=1,2,⋯,N(6.4.1)
其中约束条件 m j m_j mj和 n j n_j nj可微。
令原问题为 p ∗ \color{blue}p^* p∗ ,其最优解为 x ∗ \color{blue}x^* x∗。 - 对偶问题
对原问题使用拉格朗日乘子法:
L ( x , λ , η ) = f ( x ) + ∑ i = 1 M λ i m i + ∑ j = 1 N η i n j (6.4.2) L(x, \lambda, \eta)=f(x) +\sum_{i=1}^M\lambda_im_i + \sum_{j=1}^N\eta_in_j\tag{6.4.2} L(x,λ,η)=f(x)+i=1∑Mλimi+j=1∑Nηinj(6.4.2)
令: g ( λ , η ) = min x L ( x , λ , η ) \color{blue}g(\lambda,\eta)=\underset {x}{\min} L(x, \lambda,\eta) g(λ,η)=xminL(x,λ,η)
其对偶问题为:
{ m a x λ , η g ( λ , η ) s . t . λ i ≥ 0 (6.4.3) \begin{cases} \underset{\lambda,\eta}{max}\ g(\lambda, \eta)\\ s.t. \ \ \lambda_i \ge0 \end{cases}\tag{6.4.3} ⎩⎨⎧λ,ηmax g(λ,η)s.t. λi≥0(6.4.3)
令对偶问题最优解 d ∗ \color{blue}d^{*} d∗对应 λ ∗ \color{blue}\lambda ^{*} λ∗和 η ∗ \color{blue}\eta ^{*} η∗。
- 当目标优化问题为凸优化(convex)并满足slater条件,则可以推出其满足强对偶关系;
- 强对偶与KKT条件互为充要条件,并通过KKT条件可以求解强对偶问题。
则:
c o n v e t + s l a t e r ⇒ s t r o n g d u a l i t y ⇔ K K T \color{red}convet + slater \Rightarrow strong \ duality \Leftrightarrow KKT convet+slater⇒strong duality⇔KKT
6.4.2 KKT条件
KKT条件分为三类:可行条件、互补松弛条件、梯度为0。即:
{ 可 行 条 件 : { m i ( x ) ≤ 0 n i ( x ) = 0 λ ∗ ≥ 0 互 补 松 弛 : λ i m i = 0 梯 度 为 0 : ∂ L ∂ x ∣ x = x ∗ = 0 (6.4.4) \color{red}\begin{cases} 可行条件: \begin{cases} m_i(x)\le 0\\ n_i(x)=0\\ \lambda^*\ge 0 \end{cases} \\ 互补松弛:\lambda_im_i=0 \\ 梯度为0:{\partial L\over \partial x}|_{x=x^*}=0 \end{cases}\tag{6.4.4} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧可行条件:⎩⎪⎨⎪⎧mi(x)≤0ni(x)=0λ∗≥0互补松弛:λimi=0梯度为0:∂x∂L∣x=x∗=0(6.4.4)
- 可行性
需要满足可行性约束条件,并且需满足隐含条件 λ ∗ ≥ 0 \lambda^*\ge0 λ∗≥0,原因在6.1.1中介绍过。 - 互补松弛条件和梯度为0
d ∗ = m a x λ , η g ( λ , η ) = g ( λ ∗ , η ∗ ) = m i n x L ( x , λ ∗ , η ∗ ) ≤ L ( x ∗ , λ ∗ , η ∗ ) = f ( x ∗ ) + ∑ i = 1 M λ i ∗ m i ( x ∗ ) + ∑ j = 1 N η j ∗ n j ( x ∗ ) ⏟ = 0 = f ( x ∗ ) + ∑ i = 1 M λ i ∗ m i ( x ∗ ) ⏟ ≤ 0 ≤ f ( x ∗ ) = p ∗ d^{*}=\underset{\lambda ,\eta }{max}\; g(\lambda ,\eta ) = g(\lambda ^{*},\eta ^{*})\\ =\underset{x}{min}\; L(x,\lambda ^{*},\eta ^{*}) \leq L(x^{*},\lambda ^{*},\eta ^{*})\\ =f(x^{*})+\sum_{i=1}^{M}\lambda _{i}^{*}m_{i}(x^{*})+\underset{=0}{\underbrace{\sum_{j=1}^{N}\eta _{j}^{*}n_{j}(x^{*})}}\\ =f(x^{*})+\underset{\leq 0}{\underbrace{\sum_{i=1}^{M}\lambda _{i}^{*}m_{i}(x^{*})}} \leq f(x^{*}) =p^{*} d∗=λ,ηmaxg(λ,η)=g(λ∗,η∗)=xminL(x,λ∗,η∗)≤L(x∗,λ∗,η∗)=f(x∗)+i=1∑Mλi∗mi(x∗)+=0 j=1∑Nηj∗nj(x∗)=f(x∗)+≤0 i=1∑Mλi∗mi(x∗)≤f(x∗)=p∗
因为 d ∗ = p ∗ d^{*}=p^{*} d∗=p∗,所以上式中两个 ≤ \leq ≤都必须取等号:- 首先 m i n x L ( x , λ ∗ , η ∗ ) = L ( x ∗ , λ ∗ , η ∗ ) \underset{x}{min}\; L(x,\lambda ^{*},\eta ^{*})=L(x^{*},\lambda ^{*},\eta ^{*}) xminL(x,λ∗,η∗)=L(x∗,λ∗,η∗),则可以得出: ∂ L ( x , λ ∗ , η ∗ ) ∂ x ∣ x = x ∗ = 0 \color{blue}\left.\begin{matrix} \frac{\partial L(x,\lambda ^{*},\eta ^{*})}{\partial x} \end{matrix}\right|_{x=x^{*}}=0 ∂x∂L(x,λ∗,η∗)∣∣∣x=x∗=0。
- 然后 f ( x ∗ ) + ∑ i = 1 M λ i ∗ m i ( x ∗ ) = f ( x ∗ ) f(x^{*})+\sum_{i=1}^{M}\lambda _{i}^{*}m_{i}(x^{*})=f(x^{*}) f(x∗)+∑i=1Mλi∗mi(x∗)=f(x∗),则可以得出: ∑ i = 1 M λ i ∗ m i ( x ∗ ) = 0 \sum_{i=1}^{M}\lambda _{i}^{*}m_{i}(x^{*})=0 ∑i=1Mλi∗mi(x∗)=0,由于 λ i ∗ m i ( x ∗ ) ≤ 0 \lambda _{i}^{*}m_{i}(x^{*})\leq 0 λi∗mi(x∗)≤0,要使得 ∑ i = 1 M λ i ∗ m i ( x ∗ ) = 0 \sum_{i=1}^{M}\lambda _{i}^{*}m_{i}(x^{*})=0 ∑i=1Mλi∗mi(x∗)=0,则必有 λ i ∗ m i ( x ∗ ) = 0 \color{blue}\lambda _{i}^{*}m_{i}(x^{*})=0 λi∗mi(x∗)=0。
以上说明了KKT条件为什么与强对偶关系互为充要条件。即: c o n v e t + s l a t e r ⇒ s t r o n g d u a l i t y ⇔ K K T (6.4.5) \color{red}convet + slater \Rightarrow strong \ duality \Leftrightarrow KKT\tag{6.4.5} convet+slater⇒strong duality⇔KKT(6.4.5)
6.5 总结
- 硬SVM
对于严格可分的数据集,可以使用硬间隔SVM选择一个超平面,保证所有数据到这个超平面的距离最大。由于此问题为凸优化并且所有的约束条件都是仿射函数,故满足slater条件,可以转化为对偶问题进行求解:
{ max λ − 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j x i T x j + ∑ i = 1 N λ i s . t . λ i ≥ 0 ∑ i = 1 N λ i y i = 0 (6.5.1) \begin{cases} \underset{\lambda}{\max} \ -{1\over2}\sum_{i=1}^N\sum_{j=1}^N \lambda_i\lambda_jy_iy_jx_i^Tx_j+\sum_{i=1}^N\lambda_i\\ s.t. \ \ \lambda_i\ge 0 \\ \ \ \ \ \ \ \ \ \sum_{i=1}^N \lambda_iy_i=0 \end{cases}\tag{6.5.1} ⎩⎪⎨⎪⎧λmax −21∑i=1N∑j=1NλiλjyiyjxiTxj+∑i=1Nλis.t. λi≥0 ∑i=1Nλiyi=0(6.5.1)
求解时需要使用KKT条件(其与强对偶关系互为充要条件):
{ ∂ L ∂ w = 0 , ∂ L ∂ b = 0 , ∂ L ∂ λ = 0 λ i ( 1 − y i ( w T x i + b ) ) = 0 λ i ≥ 0 1 − y i ( w T x i + b ) ≤ 0 (6.5.2) \begin{cases} {\partial L \over \partial w}=0, {\partial L \over \partial b}=0, {\partial L \over \partial \lambda}=0\\ \lambda_i(1-y_i(w^Tx_i+b))=0\\ \lambda_i \ge 0\\ 1-y_i(w^Tx_i+b) \le0 \end{cases}\tag{6.5.2} ⎩⎪⎪⎪⎨⎪⎪⎪⎧∂w∂L=0,∂b∂L=0,∂λ∂L=0λi(1−yi(wTxi+b))=0λi≥01−yi(wTxi+b)≤0(6.5.2)
求解可得:- w ∗ = ∑ i = 1 N λ i y i x i \color{red}w^*=\sum_{i=1}^N\lambda_iy_ix_i w∗=∑i=1Nλiyixi
- b ∗ = y k − ∑ i = 1 N λ i y i x i T x k \color{red}b^*=y_k-\sum_{i=1}^N\lambda_iy_ix_i ^Tx_k b∗=yk−∑i=1NλiyixiTxk
- 软SVM
当数据集中有噪声时,可以采用软间隔SVM,允许有一点小错误,在硬间隔SVM中加入一个错误项,即:
{ min w , b 1 2 w T w + C ∑ i = 1 N ξ i s . t . y i ( w T x i + b ) ≥ 1 − ξ i ξ i ≥ 0 (6.5.3) \begin{cases} \underset{w,b}{\min}{1 \over 2}w^Tw+C\sum_{i=1}^N\xi_i\\ s.t. \ y_i(w^Tx_i+b)\ge 1-\xi_i\\ \ \ \ \ \ \ \ \ \xi_i \ge 0 \end{cases}\tag{6.5.3} ⎩⎪⎪⎨⎪⎪⎧w,bmin21wTw+C∑i=1Nξis.t. yi(wTxi+b)≥1−ξi ξi≥0(6.5.3)
可同样使用对偶问题进行求解。
