代码随想录算法训练营第7天｜● 454.四数相加II ● 383. 赎金信 ● 15. 三数之和 ● 18. 四数之和

454.四数相加||

思路:把四个数组分为两个一组,遍历a,b,并把a+b的值存储在map中,key记录a+b的值,value记录a+b出现的次数。若要四数相加为0,则c+d与a+b需要互为相反数,即a+b=-(c+d)，然后遍历c,d并在map中查找是否有a+b = -(c+d),若有则把key为-(c+d)或a+b的value(该值出现的次数)加入计数器.时间复杂度为O()

本题用map的好处是当出现索引下标值比较大时,不会像数组需要定一个很大的空间。

代码:

int fourSumCount(vector& nums1, vector& nums2, vector& nums3, vector& nums4) {
        unordered_map map;//key:a+b的数值
                                    //value：a+b出现的次数
        for(int a:nums1){//统计nums1和nums2数组中两元素之和出现的次数,统计在map中
            for(int b:nums2){
                map[a+b]++;
            }
        }
        int count = 0;//记录四数相加为0的次数
        for(int c:nums3){
            for(int d:nums4){
                if(map.find(0 - (c + d)) != map.end() ){//判断集合中是否有a+b = -（c+d）
                    count += map[0 - (c + d)];//加上该值的value既该值出现的次数
                }
            }
        }
        return count;
    }

tip:对于map的value访问方法,可以把map当成一个数组,key是数组下标,value是其里面的值,则map[key]就是在访问其value

383.赎金信

思路：本题与242.有效字母异位词解法相似.通过一个数组记录26个字母的出现次数,再遍历另一个string,使其字母的出现次数减一,但注意最后判断是否可组成,是判断数组中的值是否为负数,负数就代表该字母在之前没有出现过或者不够用,则肯定无法组成.不能判断数组全0,因为有些字母可能不会被用到。

tip：为什么本题不用map,因为只用到26个int空间,如果用map记录数据显然小题大做,map还需要花费空间和时间维护其树和哈希表.

代码：

bool canConstruct(string ransomNote, string magazine) {
        int record[26] = {0};//记录字母出现次数
        if(ransomNote.size() > magazine.size()){
            return false;//如果f的长度比m大,则m肯定不能组成f,因为一个字母只能使用一次
        }
        for(int i=0;i < magazine.size();i++){//统计magazine中字母出现的次数
            record[magazine[i] - 'a']++;
        }
        for(int i=0;i < ransomNote.size();i++){//相应的字母出现次数减1
            record[ransomNote[i] - 'a']--;
        }
        for(int j:record){//判断数组是否都为0
            if(j < 0){
                return false;
            }
        }
        return true

15.三数之和

优解一:双指针法,先将数组升序排序,a外层循环遍历整个数组,内层设定b和c,然后a固定,b和c不断内缩寻找符合条件a+b+c=0.时间复杂度O(),空间复杂度O(1)

本题最重要的还是去重。

a的去重能否把条件nums[i]==nums[i-1]改为nums[i]==nums[i+1]?

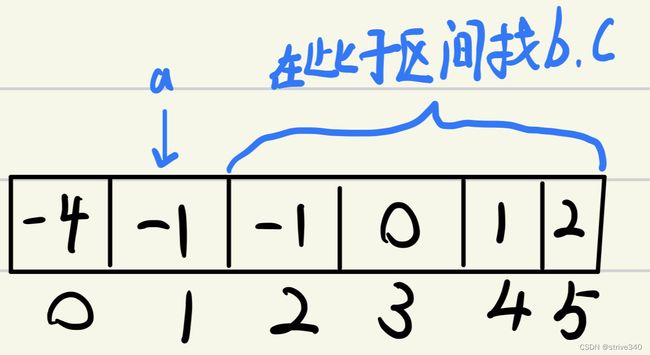
答案是不能,假如数组[-4,-1,-1,0,1,2],当a在下标为1时,把条件修改为后者,此时会判断下标为1和下标为2的a值为重复,则会跳过,但是当a=-1时,显然会有符合a+b+c=0的结果,所以不能修改条件.再来看若不修改条件,当a在下标为1时,执行查找b和c的遍历,此时会出现两个结果[-1,0,1]和[-1,-1,2]，然后a再循环到下标为2,此时a重复,y因为先前a为该值时，在left和right区间已经找出了所有符合结果的元组,当a是重复值时,则无需再查找直接跳过。(也可以解释为a=-1在下标为1时,在下标2～5的子区间已经找到了所有符合的结果,若a=-1在下标为2,由于都为-1,查找的结果都是相同的,则不需要在3～5的子区间再查找了,直接跳过）。如图解:

代码:

vector> threeSum(vector& nums) {
        vector> result;
        sort(nums.begin(),nums.end());//数组升序排序
        for(int i = 0;i < nums.size();i++){//a=nums[i],b=nums[left],c=nums[right]
            if(nums[i] > 0){//如果a大于0,则后面的元素肯定都大于0,则不需要再找
                return result;
            }
            if(i > 0 && nums[i] == nums[i-1]){//a去重
                continue;
            }
            int left = i+1;
            int right = nums.size()-1;
            while(left < right){//找b和c
                if(nums[i] + nums[left] + nums[right] > 0){//和过大,应缩小
                    right--;
                }
                else if(nums[i] + nums[left] + nums[right] < 0){//和过小,应增大
                    left++;
                }
                else{//符合三数相加
                    result.push_back(vector{nums[i],nums[left],nums[right]});
                    while(left < right && nums[right] == nums[right-1])//c去重
                        right--;
                    while(left < right && nums[left] == nums[left+1])//b去重
                        left++;
                    //当前找到答案,双指针内缩
                    right--;
                    left++;
                }
            }
        }
        return result;
    }

解二:哈希法,该题哈希法复杂且bug多

代码：.......?

18.四数之和

思路和三数之和是相同的,无非多了一个循环,三数之和是外层循环固定a,在内层找符合条件的b和c。四数之和是一样的，最外层循环固定a,外层固定b,在最内层查找c和d符合a+b+c+d=targe。

时间复杂度O()，空间复杂度O(1)

若五,六,七数之和都是一样的解法.

代码:

vector> fourSum(vector& nums, int target) {
        vector> result;
        sort(nums.begin(),nums.end());
        for(int i = 0;i < nums.size();i++){//固定a
            if(nums[i] > target){
                return result;
            }
            if(i > 0 && nums[i] == nums[i-1]){//a去重
                continue;
            }
            for(int j = i+1; j < nums.size();j++){//固定b
                if(j > i+1 && nums[j] == nums[j-1]){//b去重
                    continue;
                }
                int left = j+1;
                int right = nums.size()-1;
                while(left < right){
                    if(nums[i]+nums[j]+nums[left]+nums[right] > target){
                        right--;
                    }
                    else if(nums[i]+nums[j]+nums[left]+nums[right] < target){
                        left++;
                    }
                    else{
                        result.push_back(vector{nums[i],nums[j],nums[left],nums[right]});
                        while(left < right && nums[right] == nums[right-1])//c去重
                            right--;
                        while(left < right && nums[left] == nums[left+1])//d去重
                            left++;
                        right--;
                        left++;
                    }
                }
            }
        }
        return result;
    }