面试前需要巩固的算法知识点(自用,更新中)
文章目录
- 前言
- 零、常规算法知识
-
- 1. 什么二分法?
- 一、排序
-
- 1.有哪些排序算法,排序算法的稳定性、空间复杂度和时间复杂度
- 2.常考排序算法代码实现
- 3.什么时候用快速排序,什么时候用插入排序?
- 4.快速排序什么情况下会有最坏的时间复杂度?如何优化?
- 二、图论
-
- 1.并查集
- 2.最小生成树
- 3.最短路径
- 三、高级数据结构
-
- 1.字典树
- 2.跳表
- 3.树状数组
- 4.AVL树、红黑树、B+树
- 四、手撕代码相关
-
- 1.HOT100
- 2.剑指offer
- 3.力扣其他题
- 4.不是力扣上的题但比较高频的手撕
- 5.其他算法或智力题
-
- **洗牌算法**
- 抽奖算法
- **不用for统计一个整型中有多少个1**
- **大量数组,有限缓存空间,怎么排序?**
- **判断一个图中是否有环**
- **M个苹果放到N个盘子中,有几种放法?**
- 12个球,有1个球重量不一样,一个天平,最少几次找到特殊的球以及它和其他球比是轻还是重?
- 总结
前言
面试前自己不太熟的算法相关知识点,需要巩固
零、常规算法知识
1. 什么二分法?
二分法是一种算法思想。你们可能听过二分查找,其输入是一个有序的元素列表。如果要查找的元素包含在列表中,二分查找返回其位置;否则返回-1,这是最经典的二分法。所以你们可能认为二分法就一定要有序,答案不一定!二分只是一种思想,只要你能找到一个能支撑二分的规则,就可以利用二分法的思路去求解。
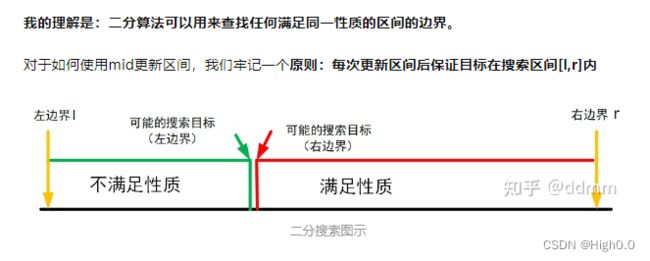
二分法就是可以把数组分成两类,要么属于这一类,要么属于那一类,没有其他的选择。见下图
一、排序
1.有哪些排序算法,排序算法的稳定性、空间复杂度和时间复杂度
2.常考排序算法代码实现
冒泡排序
算法描述:选取最大元素放到相应位置,一共进行n-1轮。
void BubbleSort(vector<int>& nums) {
int n = nums.size();
for (int i = 0; i < n - 1; ++i) {
for (int j = 0; j < n - 1 - i; ++j) {
if (nums[j + 1] < nums[j]) {
swap(nums[j], nums[j + 1]);
}
}
}
}
插入排序
算法描述:找到当前元素在已排序序列中的位置,并插入。
void InsertSort(vector<int>& nums) {
int n = nums.size();
int j, cur;
for (int i = 1; i < n; ++i) {
j = i - 1;
cur = nums[i];
while (j >= 0 && nums[j] > cur) {
nums[j + 1] = nums[j];
--j;
}
nums[j + 1] = cur;
}
}
归并排序
算法描述:分治的思想,先分再合。
void __Merge(vector<int>& nums, int p, int q, int r) {
//临时数组
vector<int> tmp(r + 1 - p, 0);
//设置各个起点
int i = p, j = q + 1, k = 0;
//合并两个有序数组
while (i <= q && j <= r) {
if (nums[i] <= nums[j])
tmp[k++] = nums[i++];
else
tmp[k++] = nums[j++];
}
int start = i, end = q;
if (start > end) {
start = j;
end = r;
}
while (start <= end) {
tmp[k++] = nums[start++];
}
//将排序好的数据拷贝到原始数组中
int n = tmp.size();
for (int c = 0; c < n; ++c) {
nums[c + p] = tmp[c];
}
}
void __MergeSort(vector<int>& nums, int p, int r) {
//终止条件
if (p >= r) return;
//求分界点
int q = p + (r - p) / 2;
//先分
__MergeSort(nums, p, q);
__MergeSort(nums, q + 1, r);
//再和
__Merge(nums, p, q, r);
}
void MergeSort(vector<int>& nums) {
__MergeSort(nums, 0, nums.size() - 1);
}
快速排序
算法描述:先分再合,每次分的时候,随机选取键值,将比键值小的元素分为一块,比键值大的元素分为另一块。
int __Partition(vector<int>& nums, int p, int r) {
//随机选取键值
int random_idx = rand() % (r + 1 - p) + p;
swap(nums[r], nums[random_idx]);
int pivot = nums[r];
//比键值小的元素分一块,大的另一块
int i = p;
for (int j = p; j <= r - 1; ++j) {
if (nums[j] < pivot) {
swap(nums[i], nums[j]);
++i;
}
}
swap(nums[i], nums[r]);
//返回分界点
return i;
}
void __QuickSort(vector<int>& nums, int p, int r) {
//终止条件
if (p >= r) return;
//先分
int q = __Partition(nums, p, r);
//再合
__QuickSort(nums, p, q - 1);
__QuickSort(nums, q + 1, r);
}
void QuickSort(vector<int>& nums) {
__QuickSort(nums, 0, nums.size() - 1);
}
堆排序
算法描述:如果是升序排序,使用数据结构大顶堆,每次将堆顶元素取出放到数组末尾位置end,并且end-1;每次操作都要重新调整堆。
//end为尾后下标
void Sink(vector<int>& nums, int start, int end) {
int parent = start;
int children = parent * 2 + 1;
while (children < end) {
if (children + 1 < end && nums[children + 1] > nums[children]) {
++children;
}
if (nums[children] > nums[parent]) {
swap(nums[children], nums[parent]);
parent = children;
children = 2 * parent + 1;
}
else {
break;
}
}
}
void HeapSort(vector<int> &nums) {
int n = nums.size();
//建堆
int i;
for (i = n / 2 - 1; i >= 0; --i) {
Sink(nums, i, n);
}
//开始排序
int end = n - 1;
while (end) {
swap(nums[0], nums[end]);
Sink(nums, 0, end);
--end;
}
}
3.什么时候用快速排序,什么时候用插入排序?
大多数实际情况中,快速排序是最佳选择;
(算法第4版159页)但是对于小数组或者基本有序的数组,使用插入排序会效率更高。
4.快速排序什么情况下会有最坏的时间复杂度?如何优化?
当每次选取的键值都是最小或最大元素时,每次分块都是一边为空,一边size减一,使得快速排序的时间复杂度变为O(n2)。
改进方法:
三取样切分法(算法第4版187页),改进快速排序性能的一个方法是使用子数组的一小部分元素的中位数来切分数组。这样做得到切分更好,但代价是需要计算中位数。人们发现(经验)取样大小设为3并用大小居中的元素切分的效果更好。
比如可以选择首元素、尾元素和一个随机元素,然后选取三个数的中位数作为键值,这样就可以基本避免最坏时间复杂度的情形发生。
二、图论
1.并查集
并查集用来解决什么问题?
并查集一般用来解决连通性问题,能够判定图中的两个节点是否相连,即能否从一个节点走到另一个节点,但是并没有要求给出两者之间的连接的情况。
通俗来讲,并查集就是用来分门别类的,随机给定两个点,通过并查集的Find接口就可以判断它们是否连通。
并查集的核心代码
const int N = 100;
int father[N];
void Init() {
//每个节点初始化为自己
for (int i = 0; i < N; ++i) {
father[i] = i;
}
}
int Find(int x) {
//查找主元,并且在查找的过程中进行状态压缩
if (x != father[x]) {
father[x] = Find(father[x]);
}
return father[x];
}
bool Union(int x, int y) {
int fx = Find(x), fy = Find(y);
if (fx == fy) return false;
//合并
father[fx] = fy;
return true;
}
2.最小生成树
练习题: 力扣1584.连接所有点的最小费用
Prim算法
算法思想:从集合U的点中选取一条权值最小的边作为起点u,并且将u能走到的所有点v加入集合U。往复此操作。
Prim算法模板
#define maxn 1000
int matrix[maxn][maxn];
int vi[maxn];
int cost[maxn];
int Prim(int n){
cost[0] = 0; //起点
int i, j, u, v;
int min_cost;
int sum = 0;
for(i = 1; i <= n; ++i){
min_cost = INT_MAX;
for(j = 0; j < n; ++j){
if(!vi[j] && cost[j] != -1 && cost[j] < min_cost){
min_cost = cost[j];
u = j;
}
}
if(min_cost == INT_MAX) break;
sum += min_cost;
vi[u] = 1;
for(v = 0; v < n; ++v){
if(!vi[v] && matrix[u][v] != -1 && (cost[v] == -1 || cost[v] > matrix[u][v])){
cost[v] = matrix[u][v];
}
}
}
return sum;
}
Kruscal算法
算法思想:将所有边进行升序排序,然后利用并查集,如果两点连通就跳过,否则就加入最小生成树。
Kruscal算法流程
1 Edge(u, v, w)放进数组中并按w进行排序
2 遍历数组,查看u和v是否在一个连通域中,不是则将这条边加入最小生成树
3.最短路径
练习题: 力扣743. 网络延迟时间
Dijstra算法:
使用邻接矩阵
和Prim算法类似,也是一个贪心的思想,选择一个未到达的最短路径作为起点 u,对所有 u 能到达的 v 进行稀疏操作。

Floyd算法:
Floyd算法是经典的动态规划算法,通过三重循环迭代地获得两点之间的最小路径。
迭代公式:其中k表示第k轮迭代。
![]()
const int maxn = 100; //节点个数
int dist[maxn][maxn];
for(k = 0; k < maxn; k++){
//v为起点
for(v = 0 ; v < maxn; v++){
//w为终点
for(w =0; w < maxn; w++){
if(dist[v][w] > (dist[v][k] + dist[k][w]))
dist[v][w] = dist[v][k] + dist[k][w];//更新为最小路径
}
}
}
SPFA算法:
使用广度优先搜索的方式对dist矩阵进行稀疏操作。
#define maxn 100
int matrix[maxn][maxn]; //邻接矩阵,matrix[i][j]记录 i 和 j 之间的开销 w
int dist[maxn]; //dist 距离数组
int Spfa(int n, int k){
queue<int> q;
q.push(k - 1); //起点入队
dist[k - 1] = 0; //起点距离为0
int u, v, t;
while(!q.empty()){
u = q.front();
q.pop();
for(v = 0; v < n; ++v){
t = matrix[u][v];
if(t == -1) continue;
if(dist[v] == -1 || dist[u] + t < dist[v]){
dist[v] = dist[u] + t;
q.push(v);
}
}
}
int min_dist = -1;
for(int i = 0; i < n; ++i){
//遍历dist矩阵寻找最短路
}
return min_dist;
}
三、高级数据结构
1.字典树
练习题: 力扣 208. 实现 Trie (前缀树)
字典树介绍:
字典树,以空间换时间,最大的特点就是共享字符串的公共前缀来达到节省空间的目的,字典树检索长度为k的字符串的时间复杂度为O(k)。
那么问题来了,为什么不用哈希表呢?哈希表索引的时间复杂度为O(1)。
原因是字典树可以通过前缀来检索拥有此前缀的单词,提前列出搜索信息,这个功能可以使得用户体验比较好,这是哈希表没有的功能。
字典树模板:
字典树可以用指针实现,也可以用数组实现,下面给出字典树的模板
int trie[1 << 18][26]; //提前准备好字典树所需的空间
int end[1 << 18]; //记录是否到达字符串的末尾
int cnt; //节点索引
//字典树初始化
void Init() {
memset(trie, 0, sizeof(trie));
memset(end, 0, sizeof(end));
cnt = 0;
}
//构建字典树
void insert(string word) {
int p = 0; //字典树起始节点
int i;
for(auto &ch: word){
i = ch - 'a';
//如果没有通往 i 这个节点的路径,构建一个节点出来
if(!trie[p][i]) trie[p][i] = ++cnt;
//去向 i 这个节点
p = trie[p][i];
}
//来到终点,标记它
end[p] = 1;
}
bool search(string word) {
int p = 0;
int i;
for(auto &ch: word){
i = ch - 'a';
//如果没有通往 i 这个节点的路径,说明字典树中没有word这个字符串,检索失败
if(!trie[p][i]) return false;
p = trie[p][i];
}
//如果end[p] = 1,说明有word这个字符串
//如果end[p] = 0, 说明word只是字典树中某个字符串的前缀
return end[p];
}
2.跳表
3.树状数组
4.AVL树、红黑树、B+树
AVL树介绍:
AVL就是一棵平衡的二叉搜索树,平衡的就是指每一个节点的左右子树的高度相差不超过1,二叉搜索树是指二叉树的中序遍历是有序的,或者说每一个节点 root 的左子树上所有节点的值小于父亲节点 root 的值,每一个节点 root 的右子树上所有节点的值都大于父亲节点 root 的值。
由于AVL树要保证严格的平衡性,因此每次插入或者删除节点,都需要通过旋转来保证二叉树的平衡性,而旋转操作是很耗时的,因此AVL适合插入删除操作少,检索操作多的场景。
红黑树介绍:
那么插入删除操作多的场景咋办呢,所有就有了红黑树。
红黑树是一棵没那么严格的平衡二叉搜索树。它有以下几个特点:
1 节点有颜色属性,不是黑的就是红的;
2 叶子节点不存放数据;
3 根节点和叶子节点是黑色的;
4 不能有两个相邻的红色节点;
5 任意一个节点到叶子节点的所有路径中黑色节点的个数都相等。
B+树介绍:
B+树在数据库中提到的比较多,建立索引的数据结构之一就是B+树,它是一棵多叉搜索树,只有叶子节点存放数据,非叶子节点只存放索引,这样就可以使得树的高度更矮,即h更小,所以B+树适合用来检索数据存放在磁盘上的情况,因为B+树的高度低,就意味着磁盘IO的次数少。
四、手撕代码相关
1.HOT100
33.搜索旋转排序数组 (数形结合:与右界比较;再分两类)
46.全排列(递归和非递归做法)
56.合并区间(按左界排序,然后用当前区间与ans最后一个区间右界比较)
2.剑指offer
50.Pow(x, n)(迭代法快速幂 and 递归)
138.复制带随机指针的链表(链表操作)
154. 寻找旋转排序数组中的最小值 II (数组中有重复值和无重复值的做法)
3.力扣其他题
25.K 个一组翻转链表(考察链表操作,就是复杂)
31.下一个排列(二分优化)
37.解数独(回溯)
41.缺失的第一个正数(原地哈希)
43.字符串相乘(记大数相乘流程,7月29日百度二面考察到)
51.N皇后(回溯)
52. 移掉 K 位数字(贪心,利用单调不减队列)
53. 二叉树的完全性检验(BFS,出现一次儿子空节点后,不允许再出现儿子空节点)
69.x的平方根(二分法)
93.复原IP地址
129.求根节点到叶节点数字之和(DFS)
145.二叉树的后序遍历(迭代法)
150. 逆波兰表达式求值(栈模拟)
162.寻找峰值(二分,爬坡法,与mid + 1比较)
165.比较版本号(模拟,记方法)
224.基本计算器 (利用栈模拟,记思想)
227.基本计算器II(利用栈模拟,记思想,需要一个pre_sign变量)
316. 去重重复字母(利用单调栈的贪心)
384.打乱数组(洗牌算法)
450. 删除二叉搜索树中的节点 (记方法)
452. 用最少数量的箭引爆气球(按右界排序+贪心,记方法)
468.验证IP地址(回溯)
470.用Rand7()实现Rand10() (用平方做,撒豆子)
554.砖墙(前缀和+哈希)
4.不是力扣上的题但比较高频的手撕
按我的理解,序号越小越高频。尤其前五个!
1.排序算法
主要两个排序算法:快速排序,堆排序(Sink下沉操作以及建堆操作)。其他排序算法,冒泡、选择、插入以及归并最好能写。
2.单例模式实现
单例模式又分为懒汉模式和饿汉模式,主要实现:线程安全(double check)的懒汉式单例模式。
3.atoi 和 memcpy 函数实现
atoi函数功能是字符串转整型,注意考虑空格、正负号以及非法字符串。
memcpy函数功能是内存拷贝,注意内存折叠的情况。
4.string类简单实现
主要实现:成员变量,构造函数,拷贝构造函数,赋值运算符重载,析构函数。
5.智能指针shared_ptr简单实现
主要实现:成员变量,构造函数,拷贝构造函数,赋值运算符重载,析构函数。
6.写个带有移动构造函数的类
7.线程相关
例如常见的实现多线程顺序打印ABC、多线程打印数字再打印字符,循环n次,主要考察多线程编程以及多线程的同步,利用C++11 thread库(线程)、mutex库(锁)、condition_variable库(条件变量)实现。
8.生产者消费者模式实现
主要考察生产者消费者模式的概念以及多线程编程相关,同样利用C++11 thread库(线程)、mutex库(锁)、condition_variable库(条件变量)、以及队列来模拟生产者消费者模式。
5.其他算法或智力题
洗牌算法
random01()随机生成0或1,实现random(int a, int b)随机获得a和b中的一个数,使用random(int a, int b)实现洗牌算法(收藏)
原理:算出a和b之间的差距d,求得最小的bit位数,使其恰好大于d,通过random(0, 1)来置位二进制位,然后加上a,如果该值落在[a, b]之间,满足条件,否则丢掉改值,继续寻找其他值!
random
int Random01(){
return rand() % 2;
}
//计算a和b之间的距离d
int Bit(int a, int b){
int d = b - a + 1;
int bit = 0;
int n = 1;
while(n < d){
n <<= 1;
++bit;
}
return bit;
}
//
int Random(int a, int b){
int bit = Bit(a, b);
int flag, value;
while(true){
value = 0;
for(int i = 0; i < bit; ++i){
flag = Random01() << i;
value |= flag;
}
if(a + value > b) continue;
else break;
}
return value;
}
洗牌算法
void WashCards(vector<int> &cards){
int n = cards.size();
for(int i = n - 1; i >= 0; --i){
int ri = rand() % (i + 1); //随机 [0, i]
swap(cards[i], cards[ri]);
}
}
抽奖算法
场景:抽奖活动,一个人不能重复获奖,抽奖的原则就是公平
法1:random
用rand()函数选取集合中的一个人中将,如果这个人之前中奖过了,那么重新rand().
法2:利用洗牌算法
法1在选取中奖人选的时候会产生冲突,那么为了不产生冲突,我们可以采用洗牌算法,然后选取前N个人作为中奖人。
不用for统计一个整型中有多少个1
int cnt = 0;
while(num){
++cnt;
num &= (num - 1);
}
大量数组,有限缓存空间,怎么排序?
使用分治的思想,类似于力扣合并k个有序链表。
分成几个小数组,分别排序,然后从每个数组中取首元素。
判断一个图中是否有环
1 拓扑排序,入度为0的节点入队,最后查看访问的节点个数是否是n。
2 DFS,如果DFS的过程中遇到了已访问的节点,就是有环。
M个苹果放到N个盘子中,有几种放法?
int Func(int m, int n){
if(n == 0) return 0;
if(n == 1 || m <= 1) return 1;
if(n > m) return Func(m, m);
return Func(m - n, n) + Func(m, n - 1);
}
12个球,有1个球重量不一样,一个天平,最少几次找到特殊的球以及它和其他球比是轻还是重?
答:最少三次
1 :4个球一组,取两组放上天平,判断特殊的球在哪一组,记为组A
2:从A组中任取3个球,再从另外8个球中取出3个球,放上天平。
3:如果一样重,说明A组中的另外一个球是特殊的,再秤一次就ok了。
如果不一样重,可以得到两个信息:特殊的球在这三个球中;特殊的球是重还是轻。再从三个球中取两个球,放在天平两侧就ok了。