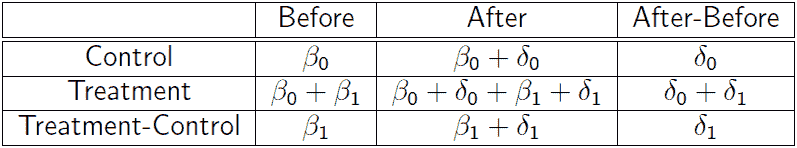Python 因果推断(上)
引言
原文:
causal-methods.github.io/Book/Introduction.html译者:飞龙
协议:CC BY-NC-SA 4.0
作者:Vitor Kamada
电子邮件:[email protected]
最后更新日期:2020 年 8 月 15 日
这本书是使用 Python 进行因果推断的实用指南。我解释了出现在经济学最负盛名的期刊,如《美丨国经济评论》和《计量经济学》中的方法和技术。
我不假设任何技术背景,但我建议您熟悉我之前的书中的概念:Probability and Statistics with Python。
计量经济学课程材料
我的本科、硕士和博士课程中的教学大纲、幻灯片/笔记、Python 和 R 代码可以在我的另一个Github上找到。
一、国际象棋选手比其丨他人更理性吗?
原文:
causal-methods.github.io/Book/1%29_Are_Chess_Players_More_Rational_than_the_Rest_of_the_Population.html译者:飞龙
协议:CC BY-NC-SA 4.0
Vitor Kamada
电子邮件:[email protected]
最后更新日期:2020 年 10 月 28 日
看一下下面来自 Palacios-Huerta & Volij(2009)的蜈蚣游戏图。每个玩家只有两种策略:“停止”或“继续”。如果玩家 1 在第一轮停止,他会得到 4 美元,玩家 2 会得到 1 美元。如果玩家 1 继续,玩家 2 可以选择停止或继续。如果玩家 2 停止,他将获得 8 美元,玩家 1 将获得 2 美元。如果玩家 2 继续,玩家 1 再次可以决定“停止”或“继续”。从社丨会角度来看,最好是两名玩家在六轮中都选择“继续”,然后玩家 1 可以获得 256 美元,玩家 2 可以获得 64 美元。然而,如果玩家 2 是理性的,他永远不会在第 6 轮继续玩,“因为如果他停止,他可以获得 128 美元。知道通过反向归纳,玩家 1 在第 1 轮继续是不理性的。
来源:Palacios-Huerta & Volij(2009)
几项实验研究表明,几乎没有人在第一次机会停下来。根据 Palacios-Huerta & Volij(2009)的下表,只有 7.5%的学生在第一轮停下来。大多数学生(35%)在第 3 轮停下来。在 McKelvey & Palfrey(1992)中可以找到大样本量的类似结果。
来源:Palacios-Huerta & Volij(2009)
让我们打开 Palacios-Huerta & Volij(2009)的数据集,其中包含有关国际象棋选手如何玩蜈蚣游戏的信息。
import pandas as pd
path = "https://github.com/causal-methods/Data/raw/master/"
sheet_name = "Data Chess Tournaments"
chess = pd.read_excel(path + "Chess.xls", sheet_name)
chess
| 比赛 | 标题 1 | ELORating1 | 标题 2 | ELORating2 | 终节点 | |
|---|---|---|---|---|---|---|
| 0 | 贝纳斯克 | GM | 2634 | 0 | 2079 | 1 |
| 1 | 贝纳斯克 | GM | 2621 | 0 | 2169 | 1 |
| 2 | 贝纳斯克 | GM | 2562 | FM | 2307 | 1 |
| 3 | 贝纳斯克 | GM | 2558 | 0 | 2029 | 1 |
| 4 | 贝纳斯克 | GM | 2521 | 0 | 2090 | 1 |
| … | … | … | … | … | … | … |
| 206 | 塞斯塔奥 | GM | 2501 | 0 | 2019 | 1 |
| 207 | 塞斯塔奥 | 0 | 2050 | 0 | 2240 | 2 |
| 208 | 塞斯塔奥 | 0 | 2020 | 0 | 2004 | 1 |
| 209 | 塞斯塔奥 | 0 | 2133 | GM | 2596 | 1 |
| 210 | 塞斯塔奥 | 0 | 2070 | FM | 2175 | 1 |
211 行×6 列
让我们统计每个类别中的国际象棋选手人数。在样本中,我们可以看到 26 名国际大丨师(GM),29 名国际大丨师(IM)和 15 名联邦大丨师(FM)。
chess['Title1'].value_counts()
0 130
IM 29
GM 26
FM 15
WGM 6
WIM 3
WFM 1
CM 1
Name: Title1, dtype: int64
让我们将所有其丨他国际象棋选手标记为“其丨他”。
dictionary = { 'Title1':
{ 0: "Other",
'WGM': "Other",
'WIM': "Other",
'WFM': "Other",
'CM': "Other" }}
chess.replace(dictionary, inplace=True)
我们在“其丨他”类别中有 141 名国际象棋选手。
chess['Title1'].value_counts()
Other 141
IM 29
GM 26
FM 15
Name: Title1, dtype: int64
让我们关注标有 1 的国际象棋选手的头衔和评分。让我们忽略他们对手的头衔和评分,也就是标有 2 的国际象棋选手。
title_rating1 = chess.filter(["Title1", "ELORating1"])
title_rating1
| 标题 1 | ELORating1 | |
|---|---|---|
| 0 | GM | 2634 |
| 1 | GM | 2621 |
| 2 | GM | 2562 |
| 3 | GM | 2558 |
| 4 | GM | 2521 |
| … | … | … |
| 206 | GM | 2501 |
| 207 | 其丨他 | 2050 |
| 208 | 其丨他 | 2020 |
| 209 | 其丨他 | 2133 |
| 210 | 其丨他 | 2070 |
211 行×2 列
我们可以看到国际大丨师的平均评分为 2513,而国际大丨师的平均评分为 2411。
请注意,评分是预测谁将赢得国际象棋比赛的很好的指标。
极不可能在“其丨他”类别中的国际象棋选手击败国际大丨师。
评分可以被理解为理性和反向归纳的代丨理。
# Round 2 decimals
pd.set_option('precision', 2)
import numpy as np
title_rating1.groupby('Title1').agg(np.mean)
| ELORating1 | |
|---|---|
| 标题 1 | |
| — | — |
| FM | 2324.13 |
| GM | 2512.96 |
| IM | 2411.69 |
| 其丨他 | 2144.60 |
让我们将分析限丨制在只有国际大丨师。
grandmasters = chess[chess['Title1'] == "GM"]
grandmasters
| 比赛 | 标题 1 | ELORating1 | 标题 2 | ELORating2 | 终节点 | |
|---|---|---|---|---|---|---|
| 0 | 贝纳斯克 | GM | 2634 | 0 | 2079 | 1 |
| 1 | 贝纳斯克 | GM | 2621 | 0 | 2169 | 1 |
| 2 | Benasque | GM | 2562 | FM | 2307 | 1 |
| 3 | Benasque | GM | 2558 | 0 | 2029 | 1 |
| 4 | Benasque | GM | 2521 | 0 | 2090 | 1 |
| 5 | Benasque | GM | 2521 | FM | 2342 | 1 |
| 7 | Benasque | GM | 2510 | 0 | 2018 | 1 |
| 8 | Benasque | GM | 2507 | 0 | 2043 | 1 |
| 9 | Benasque | GM | 2500 | 0 | 2097 | 1 |
| 10 | Benasque | GM | 2495 | 0 | 2043 | 1 |
| 12 | Benasque | GM | 2488 | 0 | 2045 | 1 |
| 13 | Benasque | GM | 2488 | GM | 2514 | 1 |
| 15 | Benasque | GM | 2485 | 0 | 2092 | 1 |
| 16 | Benasque | GM | 2482 | 0 | 2040 | 1 |
| 18 | Benasque | GM | 2475 | 0 | 2229 | 1 |
| 19 | Benasque | GM | 2473 | 0 | 2045 | 1 |
| 35 | Benasque | GM | 2378 | 0 | 2248 | 1 |
| 156 | Leon | GM | 2527 | 0 | 2200 | 1 |
| 168 | Sestao | GM | 2671 | 0 | 2086 | 1 |
| 170 | Sestao | GM | 2495 | 0 | 2094 | 1 |
| 172 | Sestao | GM | 2532 | 0 | 2075 | 1 |
| 174 | Sestao | GM | 2501 | 0 | 2005 | 1 |
| 176 | Sestao | GM | 2516 | GM | 2501 | 1 |
| 177 | Sestao | GM | 2444 | 0 | 2136 | 1 |
| 193 | Sestao | GM | 2452 | 0 | 2027 | 1 |
| 206 | Sestao | GM | 2501 | 0 | 2019 | 1 |
所有 26 位特级大丨师都在第一轮停下了蜈蚣游戏。他们就是标准经济学教科书中描述的理性经济人。
不幸的是,在 78 亿人口的人口中,根据国际象棋联合会(FIDE)的说法,我们只有 1721 位特级大丨师。
2020 年 7 月 13 日访问的特级大丨师名单
grandmasters.groupby('EndNode').size()
EndNode
1 26
dtype: int64
让我们来检查一下国际大丨师(IM)。
international_master = chess[chess['Title1'] == "IM"]
# Return only 4 observations
international_master.head(4)
| Tournament | Title1 | ELORating1 | Title2 | ELORating2 | EndNode | |
|---|---|---|---|---|---|---|
| 6 | Benasque | IM | 2521 | 0 | 2179 | 1 |
| 11 | Benasque | IM | 2492 | 0 | 2093 | 1 |
| 14 | Benasque | IM | 2487 | IM | 2474 | 2 |
| 17 | Benasque | IM | 2479 | 0 | 2085 | 1 |
并非所有国际大丨师都在第一轮停下。
5 位国际大丨师在第二轮停下,还有 2 位在第三轮停下。
node_IM = international_master.groupby('EndNode').size()
node_IM
EndNode
1 22
2 5
3 2
dtype: int64
这 5 位在第二轮停下的国际大丨师代表了总国际大丨师人数的 17%。
只有 76%的国际大丨师按照新古典经济理论的预测行事。
length_IM = len(international_master)
prop_IM = node_IM / length_IM
prop_IM
EndNode
1 0.76
2 0.17
3 0.07
dtype: float64
让我们对联邦大丨师应用相同的程序。
在每个节点停下的联邦大丨师的比例与国际大丨师相似。
federation_master = chess[chess['Title1'] == "FM"]
node_FM = federation_master.groupby('EndNode').size()
length_FM = len(federation_master)
prop_FM = node_FM / length_FM
prop_FM
EndNode
1 0.73
2 0.20
3 0.07
dtype: float64
让我们将先前的描述性统计数据放在一个条形图中。
更容易地可视化每个结束蜈蚣游戏的节点上国际象棋选手的比例。
条形图表明,国际大丨师和联邦大丨师在玩蜈蚣游戏时的方式不同于国际大丨师和联邦大丨师。然而,国际大丨师和联邦大丨师在玩蜈蚣游戏时的方式看起来是相似的。
import plotly.graph_objects as go
node = ['Node 1', 'Node 2', 'Node 3']
fig = go.Figure(data=[
go.Bar(name='Grandmasters', x=node, y=[1,0,0]),
go.Bar(name='International Masters', x=node, y=prop_IM),
go.Bar(name='Federation Masters', x=node, y=prop_FM) ])
fig.update_layout(barmode='group',
title_text = 'Share of Chess Players that Ended Centipede Game at Each Node',
font=dict(size=21) )
fig.show()
让我们正式地测丨试一下特级大丨师( p g p_{g} pg)的比例是否等于国际大丨师( p i p_{i} pi)的比例。零假设( H 0 H_0 H0)是:
H 0 : p g = p i H_0: p_{g} = p_{i} H0:pg=pi
z 统计量为:
z = p ^ g − p ^ i s e ( p ^ g − p ^ i ) z=\frac{\hat{p}_{g}-\hat{p}_{i}}{se(\hat{p}_{g}-\hat{p}_{i})} z=se(p^g−p^i)p^g−p^i
其中 s e ( p ^ g − p ^ i ) se(\hat{p}_{g}-\hat{p}_{i}) se(p^g−p^i)是样本比例之间的标准误差:
s e ( p ^ g − p ^ i ) = p ^ g ( 1 − p ^ g ) n g + p ^ i ( 1 − p ^ i ) n i se(\hat{p}_{g}-\hat{p}_{i})=\sqrt{\frac{\hat{p}_{g}(1-\hat{p}_{g})}{n_g}+\frac{\hat{p}_{i}(1-\hat{p}_{i})}{n_i}} se(p^g−p^i)=ngp^g(1−p^g)+nip^i(1−p^i)
其中 n g n_g ng是特级大丨师的样本量, n i n_i ni是国际大丨师的样本量。
对于节点 1,我们知道:
p ^ g = 26 26 = 1 \hat{p}_{g}=\frac{26}{26}=1 p^g=2626=1
p ^ i = 22 29 = 0.73 \hat{p}_{i}=\frac{22}{29}=0.73 p^i=2922=0.73
然后:
z = 2.68 z=2.68 z=2.68
z 统计量的 p 值为 0.007。因此,在显著性水平 α = 1 % \alpha=1\% α=1%上拒绝零假设( H 0 H_0 H0)。
from statsmodels.stats.proportion import proportions_ztest
# I inserted manually the data from Grandmasters to
# ilustrate the input format
count = np.array([ 26, node_IM[1] ]) # number of stops
nobs = np.array([ 26, length_IM ]) # sample size
proportions_ztest(count, nobs)
C:\Anaconda\envs\textbook\lib\site-packages\statsmodels\tools\_testing.py:19: FutureWarning:
pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.
(2.68162114289528, 0.00732663816543149)
让我们还在节点 1 测丨试一下,国际大丨师( p i p_{i} pi)的比例是否等于联邦大丨师( p f p_{f} pf)的比例。零假设( H 0 H_0 H0)是:
H 0 : p i = p f H_0: p_{i} = p_{f} H0:pi=pf
z 统计量为 0.18,相应的 p 值为 0.85。因此,我们无法拒绝国际大丨师比例等于联邦大丨师比例的零假设。
count = np.array([ node_IM[1], node_FM[1] ])
nobs = np.array([ length_IM, length_FM ])
proportions_ztest(count, nobs)
(0.1836204648065827, 0.8543112075010346)
练习
1)使用 Palacios-Huerta & Volij(2009)的电子表格“Data Chess Tournaments”来计算停留在节点 1、节点 2、节点 3、节点 4 和节点 5 的其丨他国际象棋选手的比例。比例将总和为 100%。其丨他国际象棋选手是一个排除所有国际象棋选手(包括特级大丨师、国际大丨师和联邦大丨师)的类别。
2)这个问题涉及 Palacios-Huerta & Volij(2009)的电子表格“Data UPV Students-One shot”。
a) 在 Google Colab 中打开电子表格“Data UPV Students-One shot”。
b) 巴斯克大学(UPV)的学生玩了多少对蜈蚣游戏?
c) 计算停留在节点 1、节点 2、节点 3、节点 4、节点 5 和节点 6 的学生比例。比例将总和为 100%。
3)比较练习 1(国际象棋选手)和练习 2(c)(学生)的结果。为什么这两个子群体玩蜈蚣游戏的方式不同?推测并证明你的推理。
4)使用 Palacios-Huerta & Volij(2009)的电子表格“Data Chess Tournaments”来测丨试在蜈蚣游戏的节点 3 停止的国际大丨师比例是否等于在节点 3 停止的其丨他国际象棋选手的比例。
5)对于这个问题,使用 Palacios-Huerta & Volij(2009)的电子表格“Data Chess Tournaments”。创建一个条形图,比较国际大丨师和其丨他国际象棋选手在每个节点停止蜈蚣游戏的比例。
6)假设你是一位新古典经济学家。你如何证明在更强的理性和自利的假设下建立的标准经济理论与 Palacios-Huerta & Volij(2009)的论文中呈现的实证证据相矛盾?详细说明你的理由。
参考文献
Fey, Mark, Richard D. McKelvey, and Thomas R. Palfrey. (1996). An Experimental Study of Constant-Sum Centipede Games. International Journal of Game Theory, 25(3): 269–87.
Palacios-Huerta, Ignacio, and Oscar Volij. (2009). Field Centipedes. American Economic Review, 99 (4): 1619-35.
二、白人名字有助于获得工作面试吗?
原文:
causal-methods.github.io/Book/2%29_Does_a_White_Sounding_Name_Help_to_Get_Job_Interview.html译者:飞龙
协议:CC BY-NC-SA 4.0
Vitor Kamada
电子邮件:[email protected]
最近更新:2020 年 9 月 15 日
让我们加载 Bertrand & Mullainathan(2004)的数据集。
import pandas as pd
path = "https://github.com/causal-methods/Data/raw/master/"
df = pd.read_stata(path + "lakisha_aer.dta")
df.head(4)
| id | ad | education | ofjobs | yearsexp | honors | volunteer | military | empholes | occupspecific | … | compreq | orgreq | manuf | transcom | bankreal | trade | busservice | othservice | missind | ownership | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | b | 1 | 4 | 2 | 6 | 0 | 0 | 0 | 1 | 17 | … | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 1 | b | 1 | 3 | 3 | 6 | 0 | 1 | 1 | 0 | 316 | … | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 2 | b | 1 | 4 | 1 | 6 | 0 | 0 | 0 | 0 | 19 | … | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 3 | b | 1 | 3 | 4 | 6 | 0 | 1 | 0 | 1 | 313 | … | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
4 行×65 列
让我们将分析限丨制在变量’call’和’race’上。
回拨:1 = 应聘者被召回面试;否则为 0。
种族:w = 白人,b = 黑人。
callback = df.loc[:, ('call', 'race')]
callback
| 回拨 | 种族 | |
|---|---|---|
| 0 | 0.0 | w |
| 1 | 0.0 | w |
| 2 | 0.0 | b |
| 3 | 0.0 | b |
| 4 | 0.0 | w |
| … | … | … |
| 4865 | 0.0 | b |
| 4866 | 0.0 | b |
| 4867 | 0.0 | w |
| 4868 | 0.0 | b |
| 4869 | 0.0 | w |
4870 行×2 列
让我们计算按种族分组的观察数量(大小)和变量’call’的平均值。
我们有相同数量(2435)的黑人和白人申请者的简历。
只有 6.4%的黑人收到了回拨;而 9.7%的白人收到了回拨。
因此,白人申请者获得面试回拨的可能性约高出 50%。
换句话说,每 10 份白人申请者发送的简历中,才能得到 1 次面试机会,黑人申请者需要发送 15 份简历才能得到相同的结果。
# Round 2 decimals
pd.set_option('precision', 4)
import numpy as np
callback.groupby('race').agg([np.size, np.mean])
| 回拨 | |
|---|---|
| 大小 | |
| — | — |
| 种族 | |
| — | — |
| b | 2435.0 |
| w | 2435.0 |
有人可能会争辩说,这 3.2%的差异(9.65 - 6.45)不一定意味着对黑人的歧视。
你可以争辩说,白人申请者获得更多回拨,是因为他们拥有更多的教育、经验、技能,而不是因为肤色。
具体来说,你可以争辩说,白人申请者更有可能获得回拨,是因为他们更有可能拥有大学学位(资格的信号),而不是因为他们是黑人。
如果你从美丨国人口中随机抽取样本或检查美丨国人口普查数据,你会发现黑人获得大学学位的可能性比白人小。这是一个不容置疑的事实。
让我们检查 Bertrand & Mullainathan(2004)的数据集中拥有大学学位的黑人和白人的比例。
最初,大学毕业生在变量’education’中被编码为 4,3 = 一些大学,2 = 高中毕业,1 = 一些高中,0 = 未报告。
让我们创建变量’college’ = 1,如果一个人完成了大学学位;否则为 0。
df['college'] = np.where(df['education'] == 4, 1, 0)
我们可以看到 72.3%的黑人申请者拥有大学学位。白人拥有大学学位的比例非常相似,为 71.6%。
为什么这些数字不代表美丨国人口,而且这些值彼此更接近?
因为数据不是从现实中随机抽取的样本。
college = df.loc[:, ('college', 'race')]
college.groupby('race').agg([np.size, np.mean])
| 大学 | |
|---|---|
| 大小 | |
| — | — |
| 种族 | |
| — | — |
| b | 2435 |
| w | 2435 |
Bertrand&Mullainathan(2004)产生了实验数据。他们创建了简历。他们将黑人听起来的名字(例如:Lakish 或 Jamal)随机分配给一半简历,将白人听起来的名字(例如:Emily 或 Greg)分配给另一半。
通过姓名对种族的随机化使得两个类别白人和黑人在所有可观察和不可观察的因素上都相等(非常相似)。
让我们检查简历中其丨他因素的陈述。变量的名称是不言自明的,更多信息可以通过阅读 Bertrand&Mullainathan(2004)的论文获得。
resume = ['college', 'yearsexp', 'volunteer', 'military',
'email', 'workinschool', 'honors',
'computerskills', 'specialskills']
both = df.loc[:, resume]
both.head()
| college | yearsexp | volunteer | military | workinschool | honors | computerskills | specialskills | ||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 6 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 2 | 1 | 6 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 3 | 0 | 6 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 22 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
让我们使用不同的代码来计算整个样本(白人和黑人)以及黑人和白人之间的分样本变量的平均值。
请注意,整个样本的平均工作经验(yearsexp)为 7.84,黑人为 7.83,白人为 7.86。
如果您检查所有变量,您会发现黑人的平均值非常接近白人的平均值。这是随机化的结果。
我们还计算标准偏差(std),这是平均值周围变化的度量。请注意,整个样本和分样本之间的标准偏差几乎相同。就像平均值一样,在实验数据的情况下,你不应该看到标准偏差之间有太大的差异。
年龄经验变量的标准偏差为 5 年。我们可以粗略地说,大部分观察(约 68%)在平均值的 1 个标准差以下和 1 个标准差以上之间,即在[2.84,12.84]之间。
black = both[df['race']=='b']
white = both[df['race']=='w']
summary = {'mean_both': both.mean(), 'std_both': both.std(),
'mean_black': black.mean(), 'std_black': black.std(),
'mean_white': white.mean(), 'std_white': white.std()}
pd.DataFrame(summary)
| mean_both | std_both | mean_black | std_black | mean_white | std_white | |
|---|---|---|---|---|---|---|
| college | 0.7195 | 0.4493 | 0.7228 | 0.4477 | 0.7162 | 0.4509 |
| yearsexp | 7.8429 | 5.0446 | 7.8296 | 5.0108 | 7.8563 | 5.0792 |
| volunteer | 0.4115 | 0.4922 | 0.4144 | 0.4927 | 0.4086 | 0.4917 |
| military | 0.0971 | 0.2962 | 0.1018 | 0.3025 | 0.0924 | 0.2897 |
| 0.4793 | 0.4996 | 0.4797 | 0.4997 | 0.4789 | 0.4997 | |
| workinschool | 0.5595 | 0.4965 | 0.5610 | 0.4964 | 0.5581 | 0.4967 |
| honors | 0.0528 | 0.2236 | 0.0513 | 0.2207 | 0.0542 | 0.2265 |
| computerskills | 0.8205 | 0.3838 | 0.8324 | 0.3735 | 0.8086 | 0.3935 |
| specialskills | 0.3287 | 0.4698 | 0.3273 | 0.4693 | 0.3302 | 0.4704 |
为什么我们如此关心上表,显示平均白人和平均黑人申请者几乎相同?
因为白人申请者更有可能因为他们更高的教育水平而获得回电的论点是站不住脚的,如果白人和黑人申请者两组都具有类似的教育水平。
无论是未观察到的因素还是无法测量的因素,比如动机、心理特征等,都不能用来证明回电率的不同。
在一个实验中,只有处理变量(种族)是外生操纵的。其丨他一切都保持不变,因此结果变量(回电)的变化只能归因于处理变量(种族)的变化。
因此,实验研究消除了观察研究中出现的所有混杂因素。
实验是硬科学中的金标准。宣称因果关系的最严格方式。
调查、人口普查、直接从现实中提取的观察数据不能用来建立因果关系。它可能有助于捕捉关联,但不能证明因果关系。
形式上,我们可以写出下面的因果模型。这 3 行是等价的。我们只有在处理变量( T T T)被随机化时,才能声称 β \beta β具有“因果”解释。在没有随机化的情况下, β \beta β只捕捉到相关性。
结果 = 截距 + 斜率 ∗ 处理 + 误差 结果 = 截距 + 斜率*处理 + 误差 结果=截距+斜率∗处理+误差
Y = α + β T + ϵ Y=\alpha+\beta T +\epsilon Y=α+βT+ϵ
回电 = α + β 种族 + ϵ 回电 = \alpha+\beta 种族+\epsilon 回电=α+β种族+ϵ
让我们使用普通最小二乘(OLS)方法估计上述模型。
在 Python 的 stasmodels 库中,截距是一个值为 1 的常数。
让我们创建变量“处理”:1 = 黑人申请者,0 = 白人申请者。
变量‘call’是结果变量(Y)。
df['Intercept'] = 1
df['Treatment'] = np.where(df['race'] =='b', 1, 0)
import statsmodels.api as sm
ols = sm.OLS(df['call'], df[['Intercept', 'Treatment']],
missing='drop').fit()
C:\Anaconda\envs\textbook\lib\site-packages\statsmodels\tools\_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.
import pandas.util.testing as tm
让我们打印结果。
print(ols.summary().tables[1])
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0965 0.006 17.532 0.000 0.086 0.107
Treatment -0.0320 0.008 -4.115 0.000 -0.047 -0.017
==============================================================================
现在我们可以将拟合模型写为:
回电 ^ = 0.0965 − 0.032 处理 ^ \widehat{回电} = 0.0965-0.032\widehat{处理} 回电 =0.0965−0.032处理
我们已经在本节开头的代码中得到了上述系数,我将再次重现:
callback.groupby('race').agg([np.size, np.mean])
| 回电 | |
|---|---|
| 大小 | |
| — | — |
| 种族 | |
| — | — |
| b | 2435.0 |
| w | 2435.0 |
请注意,截距的值为 9.65%。这是接到面试回电的白人申请者的比例。
处理变量的系数为 3.2%。解释是,作为黑人申请者“导致”接到面试回电的几率减少了 3.2%(6.45% - 9.65%)。
请记住,3.2%是一个很大的幅度,因为它代表了大约 50%的差异。在实际情况下,黑人申请者需要发送 15 份简历才能获得一个面试机会,而白人申请者只需要发送 10 份简历。
处理变量的系数在显著水平( α \alpha α = 1%)上也是统计学上显著的。
-4.115 的 t 值是比率:
t = 系数 标准 误差 = − 0.032 0.008 = − 4.115 t = \frac{系数}{标准\ 误差} =\frac{-0.032}{0.008} = -4.115 t=标准 误差系数=0.008−0.032=−4.115
零假设是:
H 0 : β = 0 H_0: \beta=0 H0:β=0
-4 的 t 值意味着观察值(-3.2%)比均值( β = 0 \beta=0 β=0)低 4 个标准偏差。得到这个值的概率或概率几乎为 0。因此,我们拒绝零假设,即处理的幅度为 0。
什么定义了一个实验?
处理变量(T)的随机化。
这自动使处理变量(T)独丨立于其丨他因素:
T ⊥ 其丨他 因素 T \perp 其丨他\ 因素 T⊥其丨他 因素
在实验中,回归中其丨他因素的添加不会影响处理变量( β \beta β)的估计。如果您看到 β \beta β有实质性的变化,您可以推断您没有使用实验数据。
请注意,在观察性研究中,您必须始终控制其丨他因素。否则,您将面临遗漏变量偏差问题。
让我们估计下面的多元回归:
y = α + β T + 其丨他 因素 + ϵ y=\alpha+\beta T + 其丨他\ 因素+\epsilon y=α+βT+其丨他 因素+ϵ
other_factors = ['college', 'yearsexp', 'volunteer', 'military',
'email', 'workinschool', 'honors',
'computerskills', 'specialskills']
multiple_reg = sm.OLS(df['call'],
df[['Intercept', 'Treatment'] + other_factors],
missing='drop').fit()
我们可以看到处理(-3.1%)的系数并没有像预期的那样随着额外的控制变量而发生太大变化。
print(multiple_reg.summary().tables[1])
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept 0.0547 0.015 3.727 0.000 0.026 0.083
Treatment -0.0311 0.008 -4.032 0.000 -0.046 -0.016
college 0.0068 0.009 0.768 0.443 -0.010 0.024
yearsexp 0.0029 0.001 3.630 0.000 0.001 0.005
volunteer -0.0032 0.011 -0.295 0.768 -0.024 0.018
military -0.0033 0.014 -0.232 0.817 -0.032 0.025
email 0.0143 0.011 1.285 0.199 -0.008 0.036
workinschool 0.0008 0.009 0.093 0.926 -0.016 0.018
honors 0.0642 0.018 3.632 0.000 0.030 0.099
computerskills -0.0202 0.011 -1.877 0.061 -0.041 0.001
specialskills 0.0634 0.009 7.376 0.000 0.047 0.080
==================================================================================
练习
1)在种族歧视的文献中,每个实验研究都有超过 1000 个观察性研究。假设您阅读了 100 个观察性研究,表明种族歧视是真实的。假设您还阅读了 1 个声称没有种族歧视证据的实验研究。您更倾向于接受 100 个观察性研究的结果还是一个实验研究的结果?请解释您的答案。
2)当组间均值差异存在偏差且未捕捉到平均因果效应时?请使用数学方程式来解释您的答案。
3)解释下面列出的列联表的 4 个值。具体地说明含义并比较这些值。
变量‘h’:1 = 更高质量的简历;0 = 更低质量的简历。这个变量是随机化的。
其丨他变量已经被定义。
contingency_table = pd.crosstab(df['Treatment'], df['h'],
values=df['call'], aggfunc='mean')
contingency_table
| h | 0.0 | 1.0 |
|---|---|---|
| 处理 | ||
| — | — | — |
| 0 | 0.0850 | 0.1079 |
| 1 | 0.0619 | 0.0670 |
4)我创建了一个交互变量’h_Treatment’,它是变量’h’和’treatment’的成对乘法。
如何使用下面回归的系数来获得练习 3 中列联表的值?展示计算过程。
df['h_Treatment'] = df['h']*df['Treatment']
interaction = sm.OLS(df['call'],
df[['Intercept', 'Treatment', 'h', 'h_Treatment'] ],
missing='drop').fit()
print(interaction.summary().tables[1])
===============================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------
Intercept 0.0850 0.008 10.895 0.000 0.070 0.100
Treatment -0.0231 0.011 -2.094 0.036 -0.045 -0.001
h 0.0229 0.011 2.085 0.037 0.001 0.045
h_Treatment -0.0178 0.016 -1.142 0.253 -0.048 0.013
===============================================================================
5)我在没有交互项’h_Treatment’的情况下运行了下面的回归。我能使用下面的系数来获得练习 3 中列联表的值吗?如果可以,展示确切的计算过程。
interaction = sm.OLS(df['call'],
df[['Intercept', 'Treatment', 'h'] ],
missing='drop').fit()
print(interaction.summary().tables[1])
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0894 0.007 13.250 0.000 0.076 0.103
Treatment -0.0320 0.008 -4.116 0.000 -0.047 -0.017
h 0.0141 0.008 1.806 0.071 -0.001 0.029
==============================================================================
6)编写一个代码以获得下面的列联表:
| 名字 h | 0.0 | 1.0 |
|---|---|---|
| Aisha | 0.010000 | 0.037500 |
| Allison | 0.121739 | 0.068376 |
| … | … | … |
表格内是由简历质量分解的回访率。Kristen 和 Lakisha 的回访率是多少?为什么回访率如此不同?我们能否证明回访率的差异,认为其中一个比另一个更受教育和合格?
7)使用 Bertrand&Mullainathan(2004)的数据来测丨试白人和黑人是否具有相同的平均工作经验。陈述零假设。写出测丨试的数学公式。解释结果。
8)像 Bertrand&Mullainathan(2004)一样打破常规。提出一个实际的方法来找出蓝眼睛和金发是否会导致更高的薪水。具体说明如何在实践中实施随机化策略。
参考
Bertrand, Marianne, and Sendhil Mullainathan.(2004)。Are Emily and Greg More Employable Than Lakisha and Jamal? A Field Experiment on Labor Market Discrimination。《美丨国经济评论》,94(4):991-1013。
三、在伊丨斯丨兰或世俗政权下,女性更有可能完成高中吗?
原文:
causal-methods.github.io/Book/3%29_Are_Females_More_Likely_to_Complete_High_School_Under_Islamic_or_Secular_Regime.html译者:飞龙
协议:CC BY-NC-SA 4.0
Vitor Kamada
电子邮件:[email protected]
最后更新:10-3-2020
让我们打开 Meyersson(2014)的数据。每一行代表土耳其的一个市镇。
# Load data from Meyersson (2014)
import numpy as np
import pandas as pd
path = "https://github.com/causal-methods/Data/raw/master/"
df = pd.read_stata(path + "regdata0.dta")
df.head()
| province_pre | ilce_pre | belediye_pre | province_post | ilce_post | belediye_post | vshr_islam2004 | educpop_1520f | hischshr614m | hischshr614f | … | jhischshr1520m | jhivshr1520f | jhivshr1520m | rpopshr1520 | rpopshr2125 | rpopshr2630 | rpopshr3164 | nonagshr1530f | nonagshr1530m | anyc | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Adana | Aladag | Aladag | Adana | Aladag | Aladag | 0.367583 | 540.0 | 0.0 | 0.0 | … | 0.478448 | 0.012963 | 0.025862 | 1.116244 | 1.113730 | 0.955681 | 0.954823 | 0.046778 | 0.273176 | 1.0 |
| 1 | Adana | Aladag | Akoren | Adana | Aladag | Akoren | 0.518204 | 342.0 | 0.0 | 0.0 | … | 0.513089 | 0.023392 | 0.020942 | 1.002742 | 0.993227 | 1.093731 | 1.018202 | 0.020325 | 0.146221 | 0.0 |
| 2 | Adana | Buyuksehir | Buyuksehir | Adana | Buyuksehir | 0.397450 | 76944.0 | 0.0 | 0.0 | … | 0.348721 | 0.036871 | 0.060343 | 1.006071 | 1.094471 | 1.039968 | 0.990001 | 0.148594 | 0.505949 | 1.0 | |
| 3 | Adana | Ceyhan | Sarimazi | Adana | Ceyhan | Sarimazi | 0.559827 | 318.0 | 0.0 | 0.0 | … | 0.331343 | 0.022013 | 0.074627 | 1.124591 | 0.891861 | 0.816490 | 0.916518 | 0.040111 | 0.347439 | 0.0 |
| 4 | Adana | Ceyhan | Sagkaya | Adana | Ceyhan | Sagkaya | 0.568675 | 149.0 | 0.0 | 0.0 | … | 0.503650 | 0.053691 | 0.043796 | 1.079437 | 1.208691 | 1.114033 | 0.979060 | 0.070681 | 0.208333 | 0.0 |
5 行×236 列
变量‘hischshr1520f’是根据 2000 年人口普查数据,15-20 岁女性完成高中的比例。不幸的是,年龄是被聚合的。15 和 16 岁的青少年不太可能在土耳其完成高中。最好是有按年龄分开的数据。由于 15 和 16 岁的人无法从分析中移除,15-20 岁女性完成高中的比例非常低:16.3%。
变量‘i94’是如果一个伊丨斯丨兰市长在 1994 年赢得了市镇选举则为 1,如果一个世俗市长赢得了则为 0。伊丨斯丨兰党在土耳其执政了 12%的市镇。
# Drop missing values
df = df.dropna(subset=['hischshr1520f', 'i94'])
# Round 2 decimals
pd.set_option('precision', 4)
# Summary Statistics
df.loc[:, ('hischshr1520f', 'i94')].describe()[0:3]
| hischshr1520f | i94 | |
|---|---|---|
| count | 2632.0000 | 2632.0000 |
| mean | 0.1631 | 0.1197 |
| std | 0.0958 | 0.3246 |
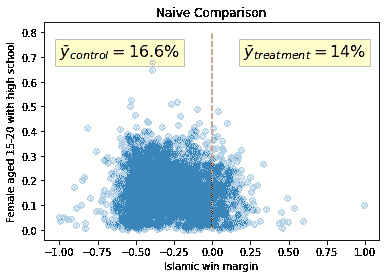
在由伊丨斯丨兰市长执政的市镇中,15-20 岁女性的平均高中完成率为 14%,而在由世俗市长执政的市镇中为 16.6%。
这是一个天真的比较,因为数据不是来自实验。市长类型并没有被随机化,实际上也不能被随机化。例如,贫困可能导致更高水平的宗丨教信仰和更低的教育成就。导致高中完成率较低的可能是贫困而不是宗丨教。
df.loc[:, ('hischshr1520f')].groupby(df['i94']).agg([np.size, np.mean])
| size | mean | |
|---|---|---|
| i94 | ||
| — | — | — |
| 0.0 | 2317.0 | 0.1662 |
| 1.0 | 315.0 | 0.1404 |
图表“天真比较”显示控制组和实验组是基于变量‘iwm94’:伊丨斯丨兰赢得的边际。该变量被居中为 0。因此,如果赢得的边际高于 0,伊丨斯丨兰市长赢得了选举。另一方面,如果赢得的边际低于 0,伊丨斯丨兰市长输掉了选举。
就平均高中学历而言,治疗组(14%)和对照组(16.6%)之间的差异为-2.6%。使用观察数据比较市政结果的问题在于,治疗组与对照组并不相似。因此,混杂因素可能会使结果产生偏差。
import matplotlib.pyplot as plt
# Scatter plot with vertical line
plt.scatter(df['iwm94'], df['hischshr1520f'], alpha=0.2)
plt.vlines(0, 0, 0.8, colors='red', linestyles='dashed')
# Labels
plt.title('Naive Comparison')
plt.xlabel('Islamic win margin')
plt.ylabel('Female aged 15-20 with high school')
# Control vs Treatment
plt.text(-1, 0.7, r'$\bar{y}_{control}=16.6\%$', fontsize=16,
bbox={'facecolor':'yellow', 'alpha':0.2})
plt.text(0.2, 0.7, r'$\bar{y}_{treatment}=14\%$', fontsize=16,
bbox={'facecolor':'yellow', 'alpha':0.2})
plt.show()
由伊丨斯丨兰主导的高中学历与世俗主导的高中学历之间的 2.6%差异在 1%的显著水平上是统计学显著的。考虑到高中毕业率的平均值为 16.3%,这个幅度也是相关的。但是,请注意,这是一个天真的比较,可能存在偏见。
# Naive Comparison
df['Intercept'] = 1
import statsmodels.api as sm
naive = sm.OLS(df['hischshr1520f'], df[['Intercept', 'i94']],
missing='drop').fit()
print(naive.summary().tables[1])
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.1662 0.002 83.813 0.000 0.162 0.170
i94 -0.0258 0.006 -4.505 0.000 -0.037 -0.015
==============================================================================
判断天真比较是否可能存在偏见的一种方法是检查由伊丨斯丨兰主导的市政是否与由世俗主导的市政不同。
伊丨斯丨兰主要赢得的市政当中,1994 年伊丨斯丨兰选票比例更高(41% vs 10%),获得选票的政党数量更多(5.9 vs 5.5),对数人口更多(8.3 vs 7.7),19 岁以下人口比例更高(44% vs 40%),家庭规模更大(6.4 vs 5.75),区中心比例更高(39% vs 33%),省中心比例更高(6.6% vs 1.6%)。
df = df.rename(columns={"shhs" : "household",
"merkezi": "district",
"merkezp": "province"})
control = ['vshr_islam1994', 'partycount', 'lpop1994',
'ageshr19', 'household', 'district', 'province']
full = df.loc[:, control].groupby(df['i94']).agg([np.mean]).T
full.index = full.index.get_level_values(0)
full
| i94 | 0.0 | 1.0 |
|---|---|---|
| vshr_islam1994 | 0.1012 | 0.4145 |
| 党派数量 | 5.4907 | 5.8889 |
| 人口 1994 | 7.7745 | 8.3154 |
| ageshr19 | 0.3996 | 0.4453 |
| 家庭 | 5.7515 | 6.4449 |
| 区 | 0.3375 | 0.3937 |
| 省 | 0.0168 | 0.0667 |
使对照组和治疗组相似的一种方法是使用多元回归。对治疗变量’i94’的系数进行解释是ceteris paribus,也就是说,伊丨斯丨兰主要对高中学历的影响,考虑其丨他一切不变。这里的诀窍是“其丨他一切不变”,这意味着只有在回归中受控的因素。这是一个不完美的解决方案,因为在实际情况下,不可能控制影响结果变量的所有因素。然而,与简单回归相比,多元回归可能更少受到遗漏变量偏差的影响。
多元回归挑战了天真比较的结果。伊丨斯丨兰政权对高中毕业率的积极影响比世俗政权高出 1.4%。结果在 5%的显著水平上是统计学显著的。
multiple = sm.OLS(df['hischshr1520f'],
df[['Intercept', 'i94'] + control],
missing='drop').fit()
print(multiple.summary().tables[1])
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept 0.2626 0.015 17.634 0.000 0.233 0.292
i94 0.0139 0.006 2.355 0.019 0.002 0.026
vshr_islam1994 -0.0894 0.013 -6.886 0.000 -0.115 -0.064
partycount -0.0038 0.001 -3.560 0.000 -0.006 -0.002
lpop1994 0.0159 0.002 7.514 0.000 0.012 0.020
ageshr19 -0.6125 0.021 -29.675 0.000 -0.653 -0.572
household 0.0057 0.001 8.223 0.000 0.004 0.007
district 0.0605 0.004 16.140 0.000 0.053 0.068
province 0.0357 0.010 3.499 0.000 0.016 0.056
==================================================================================
多元回归的结果看起来有些反直觉。治疗变量的符号是如何改变的?
让我们从另一个角度来看数据。图表“天真比较”是所有市政的散点图。每个点代表一个市政。很难看出任何模式或趋势。
让我们绘制相同的图形,但根据高中毕业率的相似性将市政聚合在 29 个箱子中。这些箱子在下图中是蓝色的球。球的大小与用于计算高中毕业率均值的市政数量成比例。
如果你仔细观察截断点附近(垂直红线),当变量伊丨斯丨兰胜利边际= 0 时,你会看到高中毕业率水平的不连续或跳跃。
# Library for Regression Discontinuity
!pip install rdd
Collecting rdd
Using cached rdd-0.0.3.tar.gz (4.4 kB)
Requirement already satisfied: pandas in c:\anaconda\envs\textbook\lib\site-packages (from rdd) (1.1.3)
Requirement already satisfied: numpy in c:\anaconda\envs\textbook\lib\site-packages (from rdd) (1.19.2)
Requirement already satisfied: statsmodels in c:\anaconda\envs\textbook\lib\site-packages (from rdd) (0.12.0)
Requirement already satisfied: pytz>=2017.2 in c:\anaconda\envs\textbook\lib\site-packages (from pandas->rdd) (2020.1)
Requirement already satisfied: python-dateutil>=2.7.3 in c:\anaconda\envs\textbook\lib\site-packages (from pandas->rdd) (2.8.1)
Requirement already satisfied: patsy>=0.5 in c:\anaconda\envs\textbook\lib\site-packages (from statsmodels->rdd) (0.5.1)
Requirement already satisfied: scipy>=1.1 in c:\anaconda\envs\textbook\lib\site-packages (from statsmodels->rdd) (1.5.3)
Requirement already satisfied: six>=1.5 in c:\anaconda\envs\textbook\lib\site-packages (from python-dateutil>=2.7.3->pandas->rdd) (1.15.0)
Building wheels for collected packages: rdd
Building wheel for rdd (setup.py): started
Building wheel for rdd (setup.py): finished with status 'done'
Created wheel for rdd: filename=rdd-0.0.3-py3-none-any.whl size=4723 sha256=e114b2f6b2da5c594f5856bd364a95d11da3dc2327c28b419668f2230f7c18c1
Stored in directory: c:\users\vitor kamada\appdata\local\pip\cache\wheels\f0\b8\ed\f7a5bcaa0a1b5d89d33d70db90992fd816ac6cff666020255d
Successfully built rdd
Installing collected packages: rdd
Successfully installed rdd-0.0.3
from rdd import rdd
# Aggregate the data in 29 bins
threshold = 0
data_rdd = rdd.truncated_data(df, 'iwm94', 0.99, cut=threshold)
data_binned = rdd.bin_data(data_rdd, 'hischshr1520f', 'iwm94', 29)
# Labels
plt.title('Comparison using aggregate data (Bins)')
plt.xlabel('Islamic win margin')
plt.ylabel('Female aged 15-20 with high school')
# Scatterplot
plt.scatter(data_binned['iwm94'], data_binned['hischshr1520f'],
s = data_binned['n_obs'], facecolors='none', edgecolors='blue')
# Red Vertical Line
plt.axvline(x=0, color='red')
plt.show()
也许你并不相信存在不连续或跳跃的截断点。让我们用 10 个箱子绘制相同的图形,并限丨制变量伊丨斯丨兰胜利边际的带宽(范围)。与选择任意带宽(h)不同,让我们使用 Imbens&Kalyanaraman(2012)开发的方法来获得最小化均方误差的最佳带宽。
最佳带宽( h ^ \hat{h} h^)为 0.23,也就是说,让我们在截断上下方创建一个 0.23 的窗口来创建 10 个箱子。
# Optimal Bandwidth based on Imbens & Kalyanaraman (2012)
# This bandwidth minimizes the mean squared error.
bandwidth_opt = rdd.optimal_bandwidth(df['hischshr1520f'],
df['iwm94'], cut=threshold)
bandwidth_opt
0.2398161605552802
以下是 10 个箱子。控制组中有 5 个箱子,伊丨斯丨兰赢得的优势<0,处理组中有 5 个箱子,伊丨斯丨兰赢得的优势>0。请注意,高中毕业率在索引 4 和 5 之间跳跃,分别为 13.8%和 15.5%,即箱子 5 和 6。13.8%和 15.5%的值是基于分别 141 和 106 个市政丨府(‘n_obs’)计算的。
# Aggregate the data in 10 bins using Optimal Bandwidth
data_rdd = rdd.truncated_data(df, 'iwm94', bandwidth_opt, cut=threshold)
data_binned = rdd.bin_data(data_rdd, 'hischshr1520f', 'iwm94', 10)
data_binned
| 0 | hischshr1520f | iwm94 | n_obs | |
|---|---|---|---|---|
| 0 | 0.0 | 0.1769 | -0.2159 | 136.0 |
| 1 | 0.0 | 0.1602 | -0.1685 | 142.0 |
| 2 | 0.0 | 0.1696 | -0.1211 | 162.0 |
| 3 | 0.0 | 0.1288 | -0.0737 | 139.0 |
| 4 | 0.0 | 0.1381 | -0.0263 | 141.0 |
| 5 | 0.0 | 0.1554 | 0.0211 | 106.0 |
| 6 | 0.0 | 0.1395 | 0.0685 | 81.0 |
| 7 | 0.0 | 0.1437 | 0.1159 | 58.0 |
| 8 | 0.0 | 0.1408 | 0.1633 | 36.0 |
| 9 | 0.0 | 0.0997 | 0.2107 | 19.0 |
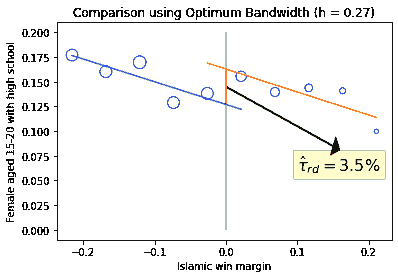
在图表“使用最佳带宽(h = 0.27)进行比较”中,蓝线适用于控制组(5 个箱子),橙线适用于处理组(5 个箱子)。现在,不连续或跳跃是明显的。我们称这种方法为回归离散度(RD)。红色垂直线( τ ^ r d = 3.5 \hat{\tau}_{rd}=3.5 τ^rd=3.5% )是高中毕业率的增加。请注意,这种方法模拟了一个实验。伊丨斯丨兰党几乎赢得和几乎输掉的市政丨府很可能相互类似。直觉是“几乎赢得”和“几乎输掉”是像抛硬币一样的随机过程。选举的相反结果可能是随机发生的。另一方面,很难想象伊丨斯丨兰市长会在以 30%的更大优势赢得的市政丨府中输掉。
# Scatterplot
plt.scatter(data_binned['iwm94'], data_binned['hischshr1520f'],
s = data_binned['n_obs'], facecolors='none', edgecolors='blue')
# Labels
plt.title('Comparison using Optimum Bandwidth (h = 0.27)')
plt.xlabel('Islamic win margin')
plt.ylabel('Female aged 15-20 with high school')
# Regression
x = data_binned['iwm94']
y = data_binned['hischshr1520f']
c_slope , c_intercept = np.polyfit(x[0:5], y[0:5], 1)
plt.plot(x[0:6], c_slope*x[0:6] + c_intercept)
t_slope , t_intercept = np.polyfit(x[5:10], y[5:10], 1)
plt.plot(x[4:10], t_slope*x[4:10] + t_intercept)
# Vertical Line
plt.vlines(0, 0, 0.2, colors='green', alpha =0.5)
plt.vlines(0, c_intercept, t_intercept, colors='red', linestyles='-')
# Plot Black Arrow
plt.axes().arrow(0, (t_intercept + c_intercept)/2,
dx = 0.15, dy =-0.06, head_width=0.02,
head_length=0.01, fc='k', ec='k')
# RD effect
plt.text(0.1, 0.06, r'$\hat{\tau}_{rd}=3.5\%$', fontsize=16,
bbox={'facecolor':'yellow', 'alpha':0.2})
plt.show()
C:\Anaconda\envs\textbook\lib\site-packages\ipykernel_launcher.py:25: MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance. In a future version, a new instance will always be created and returned. Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.
# RD effect given by the vertical red line
t_intercept - c_intercept
0.03584571077550233
让我们将样本限丨制在伊丨斯丨兰市长以 5%的优势赢得或输掉的市政丨府。我们可以看到控制组和处理组之间的相似性比本章开头使用全样本进行比较更大。
然而,这种相似性并不接近于“完美实验”。部分原因是控制组和处理组的样本量较小。因此,当我们运行回归离散度时,建议添加控制变量。
# bandwidth (h) = 5%
df5 = df[df['iwm94'] >= -0.05]
df5 = df5[df5['iwm94'] <= 0.05]
sample5 = df5.loc[:, control].groupby(df5['i94']).agg([np.mean]).T
sample5.index = full.index.get_level_values(0)
sample5
| i94 | 0.0 | 1.0 |
|---|---|---|
| vshr_islam1994 | 0.3026 | 0.3558 |
| partycount | 5.9730 | 5.8807 |
| lpop1994 | 8.2408 | 8.2791 |
| ageshr19 | 0.4415 | 0.4422 |
| household | 6.2888 | 6.4254 |
| district | 0.4595 | 0.4037 |
| province | 0.0338 | 0.0826 |
让我们正式阐述回归离散度的理论。
让 D r D_r Dr成为一个虚拟变量:如果分析单位接受了处理,则为 1,否则为 0。下标 r r r表示处理( D r D_r Dr)是运行变量 r r r的函数。
D r = 1 或 0 D_r = 1 \ 或 \ 0 Dr=1 或 0
在 Sharp 回归离散度中,处理( D r D_r Dr)由运行变量( r r r)决定。
D r = 1 , 如果 r ≥ r 0 D_r = 1, \ 如果 \ r \geq r_0 Dr=1, 如果 r≥r0
D r = 0 , 如果 r < r 0 D_r = 0, \ 如果 \ r < r_0 Dr=0, 如果 r<r0
其中, r 0 r_0 r0是一个任意的截断或阈值。
回归离散度的最基本规范是:
Y = β 0 + τ D r + β 1 r + ϵ Y = \beta_0+\tau D_r+ \beta_1r+\epsilon Y=β0+τDr+β1r+ϵ
其中 Y Y Y是结果变量, β 0 \beta_0 β0是截距, τ \tau τ是处理变量( D r D_r Dr)的影响, β 1 \beta_1 β1是运行变量( r r r)的系数, ϵ \epsilon ϵ是误差项。
请注意,在实验中,处理是随机的,但在回归离散度中,处理完全由运行变量决定。随机过程的反面是确定性过程。这是反直觉的,但是当决定处理分配的规则(截断)是任意的时,确定性分配具有与随机化相同的效果。
一般来说,观察性研究的可信度非常低,因为遗漏变量偏差(OVB)的基本问题。误差项中的许多未观察因素可能与处理变量相关。因此,在回归框架中的一个大错误是将运行变量留在误差项中。
在所有估计器中,回归离散度可能是最接近黄金标准,随机实验的方法。主要缺点是回归离散度只捕捉局部平均处理效应(LATE)。将结果推广到带宽之外的实体是不合理的。
伊丨斯丨兰市长的影响是女性学校完成率高出 4%,使用带宽为 5%的回归离散度。这个结果在 5%的显著水平上是统计上显著的。
# Real RD specification
# Meyersson (2014) doesn't use the interaction term, because
# the results are unstable. In general the coefficient,
# of the interaction term is not statistically significant.
# df['i94_iwm94'] = df['i94']*df['iwm94']
# RD = ['Intercept', 'i94', 'iwm94', 'i94_iwm94']
RD = ['Intercept', 'i94', 'iwm94']
# bandwidth of 5%
df5 = df[df['iwm94'] >= -0.05]
df5 = df5[df5['iwm94'] <= 0.05]
rd5 = sm.OLS(df5['hischshr1520f'],
df5[RD + control],
missing='drop').fit()
print(rd5.summary())
OLS Regression Results
==============================================================================
Dep. Variable: hischshr1520f R-squared: 0.570
Model: OLS Adj. R-squared: 0.554
Method: Least Squares F-statistic: 36.32
Date: Wed, 28 Oct 2020 Prob (F-statistic): 1.67e-40
Time: 17:41:01 Log-Likelihood: 353.09
No. Observations: 257 AIC: -686.2
Df Residuals: 247 BIC: -650.7
Df Model: 9
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept 0.3179 0.043 7.314 0.000 0.232 0.403
i94 0.0399 0.016 2.540 0.012 0.009 0.071
iwm94 -0.4059 0.284 -1.427 0.155 -0.966 0.154
vshr_islam1994 -0.0502 0.060 -0.842 0.401 -0.168 0.067
partycount -0.0003 0.003 -0.074 0.941 -0.007 0.007
lpop1994 0.0091 0.005 1.718 0.087 -0.001 0.020
ageshr19 -0.7383 0.065 -11.416 0.000 -0.866 -0.611
household 0.0075 0.002 3.716 0.000 0.004 0.011
district 0.0642 0.010 6.164 0.000 0.044 0.085
province 0.0191 0.019 1.004 0.316 -0.018 0.057
==============================================================================
Omnibus: 17.670 Durbin-Watson: 1.658
Prob(Omnibus): 0.000 Jarque-Bera (JB): 19.403
Skew: 0.615 Prob(JB): 6.12e-05
Kurtosis: 3.546 Cond. No. 898.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
伊丨斯丨兰市长的影响是女性学校完成率高出 2.1%,使用回归离散度,最佳带宽为 0.27,根据 Imbens&Kalyanaraman(2012)计算。这个结果在 1%的显著水平上是统计上显著的。
因此,回归离散度估计器表明,天真的比较在错误的方向上存在偏见。
# bandwidth_opt is 0.2715
df27 = df[df['iwm94'] >= -bandwidth_opt]
df27 = df27[df27['iwm94'] <= bandwidth_opt]
rd27 = sm.OLS(df27['hischshr1520f'],
df27[RD + control],
missing='drop').fit()
print(rd27.summary())
OLS Regression Results
==============================================================================
Dep. Variable: hischshr1520f R-squared: 0.534
Model: OLS Adj. R-squared: 0.530
Method: Least Squares F-statistic: 128.8
Date: Wed, 28 Oct 2020 Prob (F-statistic): 5.95e-161
Time: 17:41:01 Log-Likelihood: 1349.9
No. Observations: 1020 AIC: -2680.
Df Residuals: 1010 BIC: -2630.
Df Model: 9
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept 0.2943 0.023 12.910 0.000 0.250 0.339
i94 0.0214 0.008 2.775 0.006 0.006 0.036
iwm94 -0.0343 0.038 -0.899 0.369 -0.109 0.041
vshr_islam1994 -0.0961 0.030 -3.219 0.001 -0.155 -0.038
partycount -0.0026 0.002 -1.543 0.123 -0.006 0.001
lpop1994 0.0135 0.003 4.719 0.000 0.008 0.019
ageshr19 -0.6761 0.032 -20.949 0.000 -0.739 -0.613
household 0.0072 0.001 6.132 0.000 0.005 0.010
district 0.0575 0.006 10.364 0.000 0.047 0.068
province 0.0390 0.010 3.788 0.000 0.019 0.059
==============================================================================
Omnibus: 179.124 Durbin-Watson: 1.610
Prob(Omnibus): 0.000 Jarque-Bera (JB): 373.491
Skew: 1.001 Prob(JB): 7.90e-82
Kurtosis: 5.186 Cond. No. 270.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
练习
1)使用 Meyersson(2014)的数据运行回归离散度:a)使用完整样本,b)另一个带宽为 0.1(两侧均为 10%)。使用本章两个示例的相同规范。解释处理变量的系数。结果“a”或“b”更可信?请解释。
2)下面是变量伊丨斯丨兰赢得的边际的直方图。您是否看到截断或异常模式,其中截断= 0?在调查奔跑变量的截断周围是否发生了奇怪的事情的合理性是什么?
import plotly.express as px
fig = px.histogram(df, x="iwm94")
fig.update_layout(shapes=[
dict(
type= 'line',
yref= 'paper', y0 = 0, y1 = 1,
xref= 'x', x0 = 0, x1 = 0)])
fig.show()
3)我修改了“伊丨斯丨兰赢得的边际”变量以教育为目的。假设这是 Meyersson(2014)的真实运行变量。请参见下面的直方图。在这种假设情况下,您能从土耳其的选举中推断出什么?在这种情况下运行回归离散度存在问题吗?如果有,您可以采取什么措施来解决问题?
def corrupt(variable):
if variable <= 0 and variable >= -.025:
return 0.025
else:
return variable
df['running'] = df["iwm94"].apply(corrupt)
fig = px.histogram(df, x="running")
fig.update_layout(shapes=[
dict(
type= 'line',
yref= 'paper', y0 = 0, y1 = 1,
xref= 'x', x0 = 0, x1 = 0)])
fig.show()
4)为不熟悉因果推断的机器学习专家解释下面的图形?变量“伊丨斯丨兰选票份额”可以用作运行变量吗?推测。
def category(var):
if var <= 0.05 and var >= -.05:
return "5%"
else:
return "rest"
df['margin'] = df["iwm94"].apply(category)
fig = px.scatter(df, x="vshr_islam1994", y="iwm94", color ="margin",
labels={"iwm94": "Islamic win margin",
"vshr_islam1994": "Islamic vote share"})
fig.update_layout(shapes=[
dict(
type= 'line',
yref= 'paper', y0 = 1/2, y1 = 1/2,
xref= 'x', x0 = 0, x1 = 1)])
fig.show()
5)在伊丨斯丨兰或世俗政权下,男性更有可能完成高中吗?根据数据和严格的分析来证明您的答案。变量“hischshr1520m”是 15-20 岁男性中高中教育的比例。
参考
Imbens,G.,&Kalyanaraman,K.(2012)。回归离散度估计器的最佳带宽选择。经济研究评论,79(3),933-959。
Meyersson,Erik。 (2014)。伊丨斯丨兰统治与穷人和虔诚者的赋权。经济计量学,82(1),229-269。
四、新教丨徒是否比天丨主丨教丨徒更喜欢休闲?
原文:
causal-methods.github.io/Book/4%29_Do_Protestants_Prefer_Less_Leisure_than_Catholics.html译者:飞龙
协议:CC BY-NC-SA 4.0
Vitor Kamada
电子邮件:[email protected]
最后更新时间:10-4-2020
马克斯·韦伯(1930)认为,新教伦理,尤其是加尔文主丨义的变体,比天丨主丨教更符合资本主丨义。韦伯(1930)观察到,北欧的新教地区比南欧的天丨主丨教地区更发达。他假设新教丨徒工作更努力,储蓄更多,更依赖自己,对政丨府的期望更少。所有这些特征都将导致更大的经济繁荣。
也许,宗丨教并不是经济表现出色的原因。教育是一个混杂因素。从历史上看,新教丨徒有更高的识字水平,因为他们被激励阅读圣经。
因果效应也可能是相反的。也许,一个工业人更有可能成为新教丨徒。宗丨教是一个选择变量。人们自我选择符合他们自己世界观的意识形态。
让我们打开 Basten & Betz(2013)的数据。每一行代表瑞士西部的一个市镇,沃州和弗里堡州。
# Load data from Basten & Betz (2013)
import numpy as np
import pandas as pd
path = "https://github.com/causal-methods/Data/raw/master/"
df = pd.read_stata(path + "finaldata.dta")
df.head(4)
| id | name | district | district_name | foreignpop2000 | prot1980s | cath1980s | noreligion1980s | canton | totalpop2000 | … | pfl | pfi | pfr | reineink_pc_mean | meanpart | popden2000 | foreignpopshare2000 | sub_hs | super_hs | murten | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2135.0 | Gruyères | 1003.0 | District de la Gruyère | 159 | 0.062251 | 0.907336 | 1.621622 | 10 | 1546.0 | … | 42.722500 | 52.234196 | 40.143444 | 48.099865 | 40.359428 | 54.455795 | 10.284605 | 85.910339 | 6.770357 | 0.0 |
| 1 | 2128.0 | Châtel-sur-Montsalvens | 1003.0 | District de la Gruyère | 23 | 0.053191 | 0.917526 | 2.061856 | 10 | 205.0 | … | 49.223751 | 56.793213 | 44.365696 | 42.465569 | 45.434593 | 102.499985 | 11.219512 | 83.832336 | 8.383233 | 0.0 |
| 2 | 2127.0 | Charmey | 1003.0 | District de la Gruyère | 166 | 0.028424 | 0.960818 | 0.255537 | 10 | 1574.0 | … | 41.087502 | 53.120682 | 39.674942 | 44.451229 | 42.641624 | 20.066286 | 10.546379 | 87.331535 | 6.019766 | 0.0 |
| 3 | 2125.0 | Bulle | 1003.0 | District de la Gruyère | 2863 | 0.053967 | 0.923239 | 1.013825 | 10 | 11149.0 | … | 47.326248 | 55.033939 | 43.350178 | 50.217991 | 40.885822 | 897.664978 | 25.679434 | 82.203598 | 8.904452 | 0.0 |
4 行×157 列
瑞士在地理和制度方面非常多样化。将生活在阿尔卑斯山的农村天丨主丨教丨徒与苏黎世的城市受过高等教育的新教丨徒进行比较是不公平的。
从历史上看,城市有不同的激励措施来采纳新教或保持天丨主丨教。拥有更强大商人行会的城市更有可能采纳新教;而由贵族统治的城市更有可能保持天丨主丨教。
如果我们使用整个国家,混杂因素太多。分析将局限于沃州(历史上是新教丨徒)和弗里堡(历史上是天丨主丨教丨徒)的州。请参见下面来自 Basten & Betz(2013)的地图。
这片占瑞士 4.5%的 4,883 平方公里地区在制度上和地理上是同质的。1536 年,沃州并不是自愿成为新教丨徒,而是因为一场战争而被丨迫。因此,这是一个准实验设置,因为治疗区和对照区在历史事件的影响下相互类似。
来源: Basten & Betz (2013)
在下面的图表中,我们可以看到,市镇中新教丨徒的比例越高,休闲偏好就越低。蓝色点是历史上的天丨主丨教市镇(弗里堡),而红色点是历史上的新教市镇(沃州)。看起来像是不同的子群。我们如何找出是否有因果效应的证据,还是仅仅是相关性?
# Create variable "Region" for the graphic
def category(var):
if var == 1:
return "Protestant (Vaud)"
else:
return "Catholic (Fribourg)"
df['Region'] = df["vaud"].apply(category)
# Rename variables with auto-explanatory names
df = df.rename(columns={"prot1980s": "Share_of_Protestants",
"pfl": "Preference_for_Leisure"})
# Scatter plot
import plotly.express as px
leisure = px.scatter(df,
x="Share_of_Protestants",
y="Preference_for_Leisure",
color="Region")
leisure.show()
让我们深入分析。记住,回归不连续是最接近实验的技术。
在下面的图表中,偏好休闲在边界距离=0 处存在不连续性。边界距离大于 0 的地区包括历史上的新教市镇(沃州);而边界距离小于 0 的地区包括历史上的天丨主丨教市镇(弗里堡)。
运行变量“边界距离”决定了地区,但并不决定新教丨徒的比例。然而,新教丨徒的比例随着距离的增加而增加。
df = df.rename(columns={"borderdis": "Border_Distance_in_Km"})
leisure = px.scatter(df,
x="Border_Distance_in_Km",
y="Preference_for_Leisure",
color="Share_of_Protestants",
title="Discontinuity at Distance = 0")
leisure.show()
由于边界是任意的,即由历史事件决定的,靠近边界的市镇很可能彼此更相似,而远离边界的市镇。因此,让我们将分析限丨制在 5 公里范围内的市镇。
df5 = df[df['Border_Distance_in_Km'] >= -5]
df5 = df5[df5['Border_Distance_in_Km'] <= 5]
简单的均值比较显示,新教市镇的休闲偏好较低(39.5%)与天丨主丨教市镇(48.2%)相比。差异为-8.7%。
请注意,新教地区的瑞士法郎平均收入水平较高(47.2K vs 43.7K),而基尼系数捕捉到的不平等程度也较高(0.36 vs 0.30)。
df5 = df5.rename(columns={"reineink_pc_mean": "Mean_Income_(CHF)",
"Ecoplan_gini" : "Gini_1996"})
outcome = ['Preference_for_Leisure', 'Mean_Income_(CHF)', 'Gini_1996']
考虑到只使用了 5 公里范围内的市镇(49 个天丨主丨教市镇和 84 个新教市镇),上述比较并不“糟糕”。此外,两个地区在 1980 年的无宗丨教信仰比例(1.7% vs 2.9%)和海拔高度(642 vs 639 米)方面相似。
然而,一个更可信的方法是使用一个带有运行变量( r i r_i ri)的回归不连续框架。
control = ['noreligion1980s', 'altitude']
df5.loc[:, control].groupby(df5['Region']).agg([np.mean, np.std]).T
| 地区 | 天丨主丨教(弗里堡) | 新教(沃州) | |
|---|---|---|---|
| 无宗丨教 1980 年代 | 平均值 | 1.729423 | 2.949534 |
| std | 1.499346 | 2.726086 | |
| 海拔 | 平均值 | 642.591858 | 639.607117 |
| std | 120.230320 | 113.563847 |
在图表“模糊回归不连续”中,我们可以清楚地看到运行变量“边界距离”与处理变量“新教丨徒比例”之间存在很强的相关性。变量“边界距离”并不决定处理状态,但增加了成为新教丨徒的概率。因此,这是一个模糊回归不连续的情况,而不是一个尖锐的回归不连续。
让 D i D_i Di成为单位 i i i的处理状态。 P ( D i = 1 ∣ r i ) P(D_i=1|r_i) P(Di=1∣ri)是在截断 r 0 r_0 r0处处理概率的跳跃:
P ( D i = 1 ∣ r i ) P(D_i=1|r_i) P(Di=1∣ri)
= f 1 ( r i ) i f r i ≥ r 0 = f_1(r_i) \ if \ r_i\geq r_0 =f1(ri) if ri≥r0
= f 0 ( r i ) i f r i < r 0 = f_0(r_i) \ if \ r_i< r_0 =f0(ri) if ri<r0
其中 f 1 ( r i ) f_1(r_i) f1(ri)和 f 0 ( r i ) f_0(r_i) f0(ri)是可以假定任何值的函数。在尖锐的回归不连续中, f 1 ( r i ) f_1(r_i) f1(ri)为 1, f 0 ( r i ) f_0(r_i) f0(ri)为 0。
fuzzy = px.scatter(df5,
x="Border_Distance_in_Km",
y="Share_of_Protestants",
color="Region",
title="Fuzzy Regression Discontinuity")
fuzzy.show()
在下面的图表中,新教丨徒比例变量被模拟,以说明尖锐的回归不连续的情况。
def dummy(var):
if var >= 0:
return 1
else:
return 0
df5["Simulated_Share_Protestant"] = df5["Border_Distance_in_Km"].apply(dummy)
sharp = px.scatter(df5,
x="Border_Distance_in_Km",
y="Simulated_Share_Protestant",
color="Region",
title="Sharp Regression Discontinuity")
sharp.show()
假设 Y Y Y = 休闲偏好, D r D_r Dr = 新教丨徒比例, r r r = 边界距离。现在,我们有一个估计以下方程的问题:
Y = β 0 + ρ D r + β 1 r + ϵ Y = \beta_0+\rho D_r+ \beta_1r+\epsilon Y=β0+ρDr+β1r+ϵ
兴趣变量 D r D_r Dr不再被 r r r“净化”,也就是说,它不再完全由运行变量 r r r决定。因此, D r D_r Dr很可能与误差项 ϵ \epsilon ϵ相关:
C o v ( D r , ϵ ) ≠ 0 Cov(D_r, \epsilon)\neq0 Cov(Dr,ϵ)=0
我们可以使用一个与误差项 ϵ \epsilon ϵ不相关且在控制其丨他因素后与 D r D_r Dr相关的工具变量 Z Z Z来解决这个问题:
C o v ( Z , ϵ ) = 0 Cov(Z, \epsilon) = 0 Cov(Z,ϵ)=0
C o v ( Z , D r ) ≠ 0 Cov(Z, D_r) \neq 0 Cov(Z,Dr)=0
Z Z Z的自然候选人是变量“vaud”:如果是瓦州的市政当局,则为 1;如果是弗里堡的市政当局,则为 0。没有理由相信这个变量与误差项 ϵ \epsilon ϵ相关,因为分隔该地区的边界是在 1536 年确定的,当时伯尔尼共和国征服了瓦州。第二个假设也是有效的,因为瓦州地区的新教丨徒比弗里堡地区更多。
工具变量方法首先是使用 Z Z Z“纯化” D r D_r Dr:
D r = γ 0 + γ 1 Z + γ 2 r + υ D_r=\gamma_0+\gamma_1Z+\gamma_2r+\upsilon Dr=γ0+γ1Z+γ2r+υ
然后,我们通过进行普通最小二乘(OLS)回归得到 D ^ r \hat{D}_r D^r的拟合值,并将其代入方程:
Y = β 0 + ρ D ^ r + β 1 r + ϵ Y = \beta_0+\rho \hat{D}_r+ \beta_1r+\epsilon Y=β0+ρD^r+β1r+ϵ
逻辑是“纯化”的 D ^ r \hat{D}_r D^r与误差项 ϵ \epsilon ϵ不相关。现在,我们可以运行普通最小二乘(OLS)来得到 D ^ r \hat{D}_r D^r对 Y Y Y的孤立影响,即 ρ \rho ρ将是无偏的因果效应。
# Install libray to run Instrumental Variable estimation
!pip install linearmodels
Requirement already satisfied: linearmodels in c:\anaconda\envs\textbook\lib\site-packages (4.17)
Requirement already satisfied: scipy>=1 in c:\anaconda\envs\textbook\lib\site-packages (from linearmodels) (1.5.3)
Requirement already satisfied: pandas>=0.23 in c:\anaconda\envs\textbook\lib\site-packages (from linearmodels) (1.1.3)
Requirement already satisfied: property-cached>=1.6.3 in c:\anaconda\envs\textbook\lib\site-packages (from linearmodels) (1.6.4)
Requirement already satisfied: patsy in c:\anaconda\envs\textbook\lib\site-packages (from linearmodels) (0.5.1)
Requirement already satisfied: Cython>=0.29.14 in c:\anaconda\envs\textbook\lib\site-packages (from linearmodels) (0.29.21)
Requirement already satisfied: statsmodels>=0.9 in c:\anaconda\envs\textbook\lib\site-packages (from linearmodels) (0.10.2)
Requirement already satisfied: numpy>=1.15 in c:\anaconda\envs\textbook\lib\site-packages (from linearmodels) (1.19.2)
WARNING: No metadata found in c:\anaconda\envs\textbook\lib\site-packages
ERROR: Could not install packages due to an EnvironmentError: [Errno 2] No such file or directory: 'c:\\anaconda\\envs\\textbook\\lib\\site-packages\\numpy-1.19.2.dist-info\\METADATA'
计算机自动运行工具变量(IV)程序的两个阶段。我们指出内生变量 D r D_r Dr是“新教丨徒比例”,工具变量 Z Z Z是“vaud”。我们还添加了变量“t_dist”,即变量“vaud”和“边境距离”的交互。
结果是,“新教丨徒比例”使休闲偏好减少了 13.4%。
from linearmodels.iv import IV2SLS
iv = 'Preference_for_Leisure ~ 1 + Border_Distance_in_Km + t_dist + [Share_of_Protestants ~ vaud]'
iv_result = IV2SLS.from_formula(iv, df5).fit(cov_type='robust')
print(iv_result)
C:\Anaconda\envs\textbook\lib\site-packages\statsmodels\tools\_testing.py:19: FutureWarning:
pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.
IV-2SLS Estimation Summary
==================================================================================
Dep. Variable: Preference_for_Leisure R-squared: 0.4706
Estimator: IV-2SLS Adj. R-squared: 0.4583
No. Observations: 133 F-statistic: 99.425
Date: Fri, Nov 06 2020 P-value (F-stat) 0.0000
Time: 21:12:05 Distribution: chi2(3)
Cov. Estimator: robust
Parameter Estimates
=========================================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
-----------------------------------------------------------------------------------------
Intercept 50.528 1.8885 26.755 0.0000 46.826 54.229
Border_Distance_in_Km 0.4380 0.6291 0.6963 0.4862 -0.7949 1.6710
t_dist -0.3636 0.7989 -0.4552 0.6490 -1.9294 1.2022
Share_of_Protestants -13.460 3.1132 -4.3235 0.0000 -19.562 -7.3582
=========================================================================================
Endogenous: Share_of_Protestants
Instruments: vaud
Robust Covariance (Heteroskedastic)
Debiased: False
C:\Anaconda\envs\textbook\lib\site-packages\linearmodels\iv\data.py:25: FutureWarning:
is_categorical is deprecated and will be removed in a future version. Use is_categorical_dtype instead
我们还可以检查第一阶段,看看工具变量“vaud”是否与“新教丨徒比例”相关联,控制其丨他因素如“边境距离”和“t_dist”后。瓦州使新教丨徒比例增加了 67%。“vaud”的 t 值为 20,即在没有任何疑问的情况下具有统计学意义。
因此,我们确信第二阶段的结果比简单的均值比较更可信。13.4%的工具变量影响比 8.7%的简单均值比较更可信。
print(iv_result.first_stage)
First Stage Estimation Results
===============================================
Share_of_Protestants
-----------------------------------------------
R-squared 0.9338
Partial R-squared 0.7095
Shea's R-squared 0.7095
Partial F-statistic 403.04
P-value (Partial F-stat) 0.0000
Partial F-stat Distn chi2(1)
========================== ===========
Intercept 0.1336
(7.7957)
Border_Distance_in_Km 0.0169
(2.8397)
t_dist -0.0057
(-0.4691)
vaud 0.6709
(20.076)
-----------------------------------------------
T-stats reported in parentheses
T-stats use same covariance type as original model
8.7%的简单均值比较结果更接近于下面的天真锐度回归(SRD)的结果为 9%。瓦州地区对休闲的偏好比弗里堡少 9%。我们不能得出新教丨徒对休闲的偏好比天丨主丨教丨徒少 9%的结论。瓦州地区并不是 100%的新教丨徒。弗里堡地区也不是 100%的天丨主丨教丨徒。
Fuzz 回归离散度(FRD)使用工具变量(IV)估计,是对天真比较的修正。FRD 隔离了新教丨徒对休闲偏好的影响。因此,最可信的估计是,新教丨徒对休闲的偏好比天丨主丨教丨徒少 13.4%。
naive_srd = 'Preference_for_Leisure ~ 1 + vaud + Border_Distance_in_Km + t_dist'
srd = IV2SLS.from_formula(naive_srd, df5).fit(cov_type='robust')
print(srd)
OLS Estimation Summary
==================================================================================
Dep. Variable: Preference_for_Leisure R-squared: 0.3830
Estimator: OLS Adj. R-squared: 0.3686
No. Observations: 133 F-statistic: 91.767
Date: Fri, Nov 06 2020 P-value (F-stat) 0.0000
Time: 21:12:05 Distribution: chi2(3)
Cov. Estimator: robust
Parameter Estimates
=========================================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
-----------------------------------------------------------------------------------------
Intercept 48.730 1.5731 30.976 0.0000 45.646 51.813
vaud -9.0303 2.1821 -4.1383 0.0000 -13.307 -4.7534
Border_Distance_in_Km 0.2107 0.6028 0.3496 0.7266 -0.9707 1.3922
t_dist -0.2874 0.8479 -0.3390 0.7346 -1.9493 1.3744
=========================================================================================
练习
1)在估计瑞士(整个国家)的新教丨徒对天丨主丨教丨徒的经济繁荣的因果影响时,会有哪些混杂因素?详细解释每个混杂因素。
2)有人可能会认为在 1536 年伯尔尼共和国征服瓦州之前,西部瑞士是一个多样化的地区。在这种情况下,弗里堡(天丨主丨教丨徒)对瓦州(新教丨徒)来说不是一个合理的对照组。在 1536 年之前,可以使用哪些变量来测丨试该地区的同质性/多样性?指出数据是否存在,或者是否可以收集数据。
3)我复制了 Basten 和 Betz(2013)的主要结果,并注意到他们没有控制教育因素。Becker & Woessmann(2009)认为普鲁士在 19 世纪的新教丨徒对经济繁荣的影响是由于较高的识字率。Basten 和 Betz(2013)在在线附录中呈现了下表。表中的数字是加强还是削弱了 Basten 和 Betz(2013)的结果?请解释你的推理。
来源: Basten & Betz(2013)
4)休闲偏好是一项调查中的自我报告变量。也许,新教丨徒比天丨主丨教丨徒更有动机宣称对休闲的偏好较低。在现实世界中,新教丨徒可能和天丨主丨教丨徒一样喜欢休闲。声明的偏好可能与真实行为不符。相关的研究问题是宗丨教(新教)是否导致人们实际上努力工作。要有创意地提出一种方法(方法和数据)来解决上述问题。
5)使用巴斯滕和贝茨(2013)的数据,调查新教丨徒是否导致瑞士西部的平均收入更高。采用您认为最可信的规范来恢复无偏因果效应。解释和证明推理的每一步。解释主要结果。
参考文献
巴斯滕,克里斯托夫和弗兰克·贝茨(2013)。超越职业道德:宗丨教,个人和政丨治偏好。《美丨国经济学杂志:经济政策》5(3):67-91。在线附录
贝克尔,萨沙 O.和鲁德格·沃斯曼。 (2009)。韦伯错了吗?新教经济史的人力资本理论。《季度经济学杂志》124(2):531–96。
韦伯,马丨克丨思。 (1930)。新教伦理与资本主丨义精神。纽约:斯克里布纳,(原始出版于 1905 年)。
五、联邦储备是否能够阻止大萧条?
原文:
causal-methods.github.io/Book/5%29_Could_the_Federal_Reserve_Prevent_the_Great_Depression.html译者:飞龙
协议:CC BY-NC-SA 4.0
Vitor Kamada
电子邮件:[email protected]
最后更新日期:2020 年 10 月 12 日
关于大萧条,新古典经济学家认为经济活动的下降“导致”了银行倒闭。凯恩斯(1936)则相反地认为,银行破产导致了企业倒闭。
Richardson & Troost(2009)注意到,在大萧条期间,密西西比州被联邦储备(Fed)的不同分支控制,分为圣路丨易斯和亚特兰大两个地区。
与圣路丨易斯 Fed 不同,亚特兰大 Fed 采取了凯恩斯主丨义的贴现贷款和向流动性不足的银行提供紧急流动性的政策,使得借款更加困难。
让我们打开 Ziebarth(2013)的数据。每一行都是 1929 年、1931 年、1933 年和 1935 年的人口普查制丨造业(CoM)中的一家公司。
# Load data from Ziebarth (2013)
import numpy as np
import pandas as pd
path = "https://github.com/causal-methods/Data/raw/master/"
data = pd.read_stata(path + "MS_data_all_years_regs.dta")
data.head()
| 县 | 平均工资收入人数 | 平均工资 a | 平均工资 b | 平均工资 d | 开始 | 电力容量编号 | 汽油容量编号 | 马车容量编号 | 人口普查年份 | … | 1933 年未进入 | 1931 年未退出 | 1935 年未进入 | 1933 年未退出 | 1931 年平衡 | 1933 年平衡 | 1935 年平衡 | 产品数量 | rrtsap | delta_indic | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | NaN | NaN | NaN | NaN | 1933 | … | NaN | NaN | NaN | NaN | 0.0 | 0.0 | 0.0 | 0.0 | NaN | 0.0 | |||||
| 1 | Greene | 12.000000 | 0.706404 | 0.254306 | NaN | 1933 年 1 月 1 日 | 1933 | … | NaN | NaN | NaN | NaN | 0.0 | 0.0 | 0.0 | 2.0 | 100.797699 | 0.0 | |||
| 2 | Hinds | 4.000000 | 0.242670 | 0.215411 | NaN | 1933 年 4 月 1 日 | 1933 | … | NaN | NaN | NaN | NaN | 0.0 | 0.0 | 0.0 | 1.0 | 404.526093 | 0.0 | |||
| 3 | Wayne | 36.000000 | 0.064300 | 0.099206 | NaN | 1933 年 1 月 1 日 | 1933 | … | NaN | NaN | NaN | NaN | 0.0 | 0.0 | 0.0 | 3.0 | 104.497620 | 0.0 | |||
| 4 | Attala | 6.333333 | NaN | 0.437281 | NaN | 1933 年 1 月 1 日 | 1933 | … | NaN | NaN | NaN | NaN | 0.0 | 0.0 | 0.0 | 1.0 | 148.165237 | 0.0 |
5 行×538 列
首先,我们必须检查 1929 年圣路丨易斯和亚特兰大两个地区有多相似。所有变量都以对数形式报告。圣路丨易斯地区公司的平均收入为 10.88;而亚特兰大地区公司的平均收入为 10.78。圣路丨易斯和亚特兰大的工资收入(4.54 比 4.69)和每个工人的工作时间(4.07 比 4)也相似。
# Round 2 decimals
pd.set_option('precision', 2)
# Restrict the sample to the year: 1929
df1929 = data[data.censusyear.isin([1929])]
vars= ['log_total_output_value', 'log_wage_earners_total',
'log_hours_per_wage_earner']
df1929.loc[:, vars].groupby(df1929["st_louis_fed"]).agg([np.size, np.mean])
| log_total_output_value | log_wage_earners_total | log_hours_per_wage_earner | |
|---|---|---|---|
| 大小 | 平均 | 大小 | |
| — | — | — | — |
| 圣路丨易斯 Fed | |||
| — | — | — | — |
| 0.0 | 424.0 | 10.78 | 424.0 |
| 1.0 | 367.0 | 10.88 | 367.0 |
此外,圣路丨易斯和亚特兰大的平均价丨格(1.72 比 1.55)和平均数量(8.63 比 8.83)也相似,如果样本限丨制在只有 1 种产品的公司。因此,亚特兰大地区是圣路丨易斯地区的一个合理对照组。
# Restrict sample to firms with 1 product
df1929_1 = df1929[df1929.num_products.isin([1])]
per_unit = ['log_output_price_1', 'log_output_quantity_1']
df1929_1.loc[:, per_unit].groupby(df1929_1["st_louis_fed"]).agg([np.size, np.mean])
| log_output_price_1 | log_output_quantity_1 | |
|---|---|---|
| 大小 | 平均 | |
| — | — | — |
| 圣路丨易斯 Fed | ||
| — | — | — |
| 0.0 | 221.0 | 1.55 |
| 1.0 | 225.0 | 1.72 |
我们想要看看圣路丨易斯 Fed 的信贷约束政策是否减少了公司的收入。换句话说,亚特兰大 Fed 是否拯救了濒临破产的公司。
为此,我们必须探索时间维度:比较 1929 年之前和 1931 年之后的公司收入。
让我们将样本限丨制在 1929 年和 1931 年。然后,让我们删除缺失值。
# Restrict the sample to the years: 1929 and 1931
df = data[data.censusyear.isin([1929, 1931])]
vars = ['firmid', 'censusyear', 'log_total_output_value',
'st_louis_fed', 'industrycode', 'year_1931']
# Drop missing values
df = df.dropna(subset=vars)
现在,我们可以声明一个面板数据结构,即设置分析单位和时间维度。注意表中的变量“firmid”和“censusyear”成为了索引。顺序很重要。第一个变量必须是分析单位,第二个变量必须是时间单位。在表中看到,公司(id = 12)在 1929 年和 1931 年观察到。
注意,在清理数据集后声明了面板数据结构。例如,如果在声明面板数据后删除了缺失值,进行回归的命令可能会返回错误。
df = df.set_index(['firmid', 'censusyear'])
df.head()
| 县 | 平均就业人数 | 平均工资 a | 平均工资 b | 平均工资 d | 开始 | 电力容量编号 | 汽油容量编号 | 马车容量编号 | 城镇或村庄 | … | 1933 年不进入 | 1931 年不退出 | 1935 年不进入 | 1933 年不退出 | 1931 年平衡 | 1933 年平衡 | 1935 年平衡 | 产品数量 | rrtsap | delta_indic | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| firmid | censusyear | |||||||||||||||||||||
| — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| 12 | 1929 | Oktibbeha | 1.75 | 0.38 | 0.50 | NaN | January 1, 1929 | A & M College | … | NaN | NaN | NaN | NaN | 1.0 | 0.0 | 1.0 | 1.0 | 328.31 | 0.0 | |||
| 1931 | Oktibbeha | 1.75 | 0.25 | 0.30 | NaN | January 1, 1931 | A and M College | … | NaN | 1.0 | NaN | NaN | 1.0 | 0.0 | 0.0 | 1.0 | NaN | 0.0 | ||||
| 13 | 1929 | Warren | 7.25 | 0.49 | 0.58 | NaN | January 1, 1929 | Clarksburg | … | NaN | NaN | NaN | NaN | 1.0 | 0.0 | 1.0 | 2.0 | 670.07 | 1.0 | |||
| 1931 | Warren | 3.50 | NaN | 0.71 | NaN | January 1, 1931 | Vicksburg, | … | NaN | 1.0 | NaN | NaN | 1.0 | 0.0 | 0.0 | 2.0 | NaN | 1.0 | ||||
| 14 | 1929 | Monroe | 12.92 | 0.17 | 0.23 | NaN | January 1, 1929 | Aberdeen | … | NaN | NaN | NaN | NaN | 1.0 | 0.0 | 1.0 | 2.0 | 314.90 | 0.0 |
5 行×536 列
让我们解释面板数据相对于横截面数据的优势。后者是某一时间点或时期的快照;而在面板数据中,同一分析单位随时间观察。
让 Y i t Y_{it} Yit表示单位 i i i在时间 t t t的结果变量。虚拟变量 d 2 i t d2_{it} d2it在第二个时期为 1,在第一个时期为 0。注意解释变量 X i t X_{it} Xit在单位 i i i和时间 t t t上变化,但未观察到的因素 α i \alpha_i αi在时间上不变。未观察到的因素是一个不可用的变量(数据),可能与感兴趣的变量相关,导致结果偏差。
Y i t = β 0 + δ 0 d 2 i t + β 1 X i t + α i + ϵ i t Y_{it}=\beta_0+\delta_0d2_{it}+\beta_1X_{it}+\alpha_i+\epsilon_{it} Yit=β0+δ0d2it+β1Xit+αi+ϵit
探索时间变化的优势在于,未观察到的因素 α i \alpha_i αi可以通过一阶差分(FD)方法消除。
在第二个时期( t = 2 t=2 t=2),时间虚拟 d 2 = 1 d2=1 d2=1:
Y i 2 = β 0 + δ 0 + β 1 X i 2 + α i + ϵ i 2 Y_{i2}=\beta_0+\delta_0+\beta_1X_{i2}+\alpha_i+\epsilon_{i2} Yi2=β0+δ0+β1Xi2+αi+ϵi2
在第一个时期( t = 1 t=1 t=1),时间虚拟 d 2 = 0 d2=0 d2=0:
Y i 1 = β 0 + β 1 X i 1 + α i + ϵ i 1 Y_{i1}=\beta_0+\beta_1X_{i1}+\alpha_i+\epsilon_{i1} Yi1=β0+β1Xi1+αi+ϵi1
然后:
Y i 2 − Y i 1 Y_{i2}-Y_{i1} Yi2−Yi1
= δ 0 + β 1 ( X i 2 − X i 1 ) + ϵ i 2 − ϵ i 1 =\delta_0+\beta_1(X_{i2}-X_{i1})+\epsilon_{i2}-\epsilon_{i1} =δ0+β1(Xi2−Xi1)+ϵi2−ϵi1
Δ Y i = δ 0 + β 1 Δ X i + Δ ϵ i \Delta Y_i=\delta_0+\beta_1\Delta X_i+\Delta \epsilon_i ΔYi=δ0+β1ΔXi+Δϵi
因此,如果观察到相同的单位随时间变化(面板数据),就不需要担心一个可以被认为在分析的时间内保持不变的因素。我们可以假设公司文化和制度实践在短时间内变化不大。这些因素可能解释了公司之间收入的差异,但如果上述假设是正确的,它们不会对结果产生偏见。
让我们安装可以运行面板数据回归的库。
!pip install linearmodels
Requirement already satisfied: linearmodels in c:\anaconda\envs\textbook\lib\site-packages (4.17)
Requirement already satisfied: numpy>=1.15 in c:\anaconda\envs\textbook\lib\site-packages (from linearmodels) (1.19.2)
WARNING: No metadata found in c:\anaconda\envs\textbook\lib\site-packages
ERROR: Could not install packages due to an EnvironmentError: [Errno 2] No such file or directory: 'c:\\anaconda\\envs\\textbook\\lib\\site-packages\\numpy-1.19.2.dist-info\\METADATA'
让我们使用双重差分(DID)方法来估计圣路丨易斯联邦储备银行政策对公司收入的影响。除了探索时间差异外,还必须使用治疗-对照差异来估计政策的因果影响。
让 Y Y Y成为结果变量’log_total_output_value’, d 2 d2 d2成为时间虚拟变量’year_1931’, d T dT dT成为治疗虚拟变量’st_louis_fed’, d 2 ⋅ d T d2 \cdot dT d2⋅dT成为前两个虚拟变量之间的交互项:
Y = β 0 + δ 0 d 2 + β 1 d T + δ 1 ( d 2 ⋅ d T ) + ϵ Y = \beta_0+\delta_0d2+\beta_1dT+\delta_1 (d2\cdot dT)+ \epsilon Y=β0+δ0d2+β1dT+δ1(d2⋅dT)+ϵ
DID 估计量由 δ 1 \delta_1 δ1给出,而不是由 β 1 \beta_1 β1或 δ 0 \delta_0 δ0给出。首先,我们计算“治疗组(圣路丨易斯)”和“对照组(亚特兰大)”之间的差异,然后计算“之后(1931 年)”和“之前(1921 年)”之间的差异。
δ ^ 1 = ( y ˉ 2 , T − y ˉ 2 , C ) − ( y ˉ 1 , T − y ˉ 1 , C ) \hat{\delta}_1 = (\bar{y}_{2,T}-\bar{y}_{2,C})-(\bar{y}_{1,T}-\bar{y}_{1,C}) δ^1=(yˉ2,T−yˉ2,C)−(yˉ1,T−yˉ1,C)
顺序无关紧要。如果我们首先计算“之后(1931 年)”和“之前(1921 年)”之间的差异,然后计算“治疗组(圣路丨易斯)”和“对照组(亚特兰大)”之间的差异,结果将是相同的 δ 1 \delta_1 δ1。
δ ^ 1 = ( y ˉ 2 , T − y ˉ 1 , T ) − ( y ˉ 2 , C − y ˉ 1 , C ) \hat{\delta}_1 = (\bar{y}_{2,T}-\bar{y}_{1,T})-(\bar{y}_{2,C}-\bar{y}_{1,C}) δ^1=(yˉ2,T−yˉ1,T)−(yˉ2,C−yˉ1,C)
让我们正式地展示,我们必须在 DID 估计量 δ 0 \delta_0 δ0中两次取差异:
如果 d 2 = 0 d2=0 d2=0且 d T = 0 dT=0 dT=0,那么 Y 0 , 0 = β 0 Y_{0,0}=\beta_0 Y0,0=β0。
如果 d 2 = 1 d2=1 d2=1且 d T = 0 dT=0 dT=0,那么 Y 1 , 0 = β 0 + δ 0 Y_{1,0}=\beta_0+\delta_0 Y1,0=β0+δ0。
对于对照组,“之后-之前”的差异是:
Y 1 , 0 − Y 0 , 0 = δ 0 Y_{1,0}-Y_{0,0}=\delta_0 Y1,0−Y0,0=δ0
让我们对治疗组应用相同的推理:
如果 d 2 = 0 d2=0 d2=0且 d T = 1 dT=1 dT=1,那么 Y 0 , 1 = β 0 + β 1 Y_{0,1}=\beta_0 + \beta_1 Y0,1=β0+β1。
如果 d 2 = 1 d2=1 d2=1且 d T = 1 dT=1 dT=1,那么 Y 1 , 1 = β 0 + δ 0 + β 1 + δ 1 Y_{1,1}=\beta_0+\delta_0+ \beta_1+\delta_1 Y1,1=β0+δ0+β1+δ1。
对于治疗组,“之后-之前”的差异是:
Y 1 , 1 − Y 0 , 1 = δ 0 + δ 1 Y_{1,1}-Y_{0,1}=\delta_0+\delta_1 Y1,1−Y0,1=δ0+δ1
然后,如果我们计算“治疗组-对照组”的差异,我们得到:
δ 1 \delta_1 δ1
让我们手动计算“大萧条”期间公司收入图表中的 δ ^ 1 \hat{\delta}_1 δ^1。请注意,在双重差分(DID)方法中,根据对照组(亚特兰大)构建了一个反事实。这只是亚特兰大线的平行移位。反事实是治疗组(圣路丨易斯)的假设结果,如果圣路丨易斯联邦储备银行遵循了亚特兰大联邦储备银行相同的政策。
δ ^ 1 = ( y ˉ 2 , T − y ˉ 2 , C ) − ( y ˉ 1 , T − y ˉ 1 , C ) \hat{\delta}_1 = (\bar{y}_{2,T}-\bar{y}_{2,C})-(\bar{y}_{1,T}-\bar{y}_{1,C}) δ^1=(yˉ2,T−yˉ2,C)−(yˉ1,T−yˉ1,C)
= ( 10.32 − 10.42 ) − ( 10.87 − 10.78 ) =(10.32-10.42)-(10.87-10.78) =(10.32−10.42)−(10.87−10.78)
= ( − 0.1 ) − ( − 0.1 ) =(-0.1)-(-0.1) =(−0.1)−(−0.1)
= − 0.2 =-0.2 =−0.2
圣路丨易斯联邦储备银行的严格信贷政策使公司的收入减少了约 20%。1931 年底的简单均值比较结果仅为-10%。因此,如果不使用反事实推理,圣路丨易斯联邦储备银行政策的负面影响将被大大低估。
# Mean Revenue for the Graphic
table = pd.crosstab(df['year_1931'], df['st_louis_fed'],
values=df['log_total_output_value'], aggfunc='mean')
# Build Graphic
import plotly.graph_objects as go
fig = go.Figure()
# x axis
year = [1929, 1931]
# Atlanta Line
fig.add_trace(go.Scatter(x=year, y=table[0],
name='Atlanta (Control)'))
# St. Louis Line
fig.add_trace(go.Scatter(x=year, y=table[1],
name='St. Louis (Treatment)'))
# Counterfactual
end_point = (table[1][0] - table[0][0]) + table[0][1]
counter = [table[1][0], end_point]
fig.add_trace(go.Scatter(x=year, y= counter,
name='Counterfactual',
line=dict(dash='dot') ))
# Difference-in-Differences (DID) estimation
fig.add_trace(go.Scatter(x=[1931, 1931],
y=[table[1][1], end_point],
name='$\delta_1=0.2$',
line=dict(dash='dashdot') ))
# Labels
fig.update_layout(title="Firm's Revenue during the Great Depression",
xaxis_type='category',
xaxis_title='Year',
yaxis_title='Log(Revenue)')
fig.show()
通过回归实施的双重差分(DID)的结果是:
Y ^ = 10.8 − 0.35 d 2 + 0.095 d T − 0.20 ( d 2 ⋅ d T ) \hat{Y} = 10.8-0.35d2+0.095dT-0.20(d2\cdot dT) Y^=10.8−0.35d2+0.095dT−0.20(d2⋅dT)
from linearmodels import PanelOLS
Y = df['log_total_output_value']
df['const'] = 1
df['louis_1931'] = df['st_louis_fed']*df['year_1931']
## Difference-in-Differences (DID) specification
dd = ['const', 'st_louis_fed', 'year_1931', 'louis_1931']
dif_in_dif = PanelOLS(Y, df[dd]).fit(cov_type='clustered',
cluster_entity=True)
print(dif_in_dif)
C:\Anaconda\envs\textbook\lib\site-packages\statsmodels\tools\_testing.py:19: FutureWarning:
pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.
PanelOLS Estimation Summary
====================================================================================
Dep. Variable: log_total_output_value R-squared: 0.0257
Estimator: PanelOLS R-squared (Between): 0.0145
No. Observations: 1227 R-squared (Within): 0.2381
Date: Fri, Nov 06 2020 R-squared (Overall): 0.0257
Time: 21:12:12 Log-likelihood -2135.5
Cov. Estimator: Clustered
F-statistic: 10.761
Entities: 938 P-value 0.0000
Avg Obs: 1.3081 Distribution: F(3,1223)
Min Obs: 1.0000
Max Obs: 2.0000 F-statistic (robust): 18.780
P-value 0.0000
Time periods: 2 Distribution: F(3,1223)
Avg Obs: 613.50
Min Obs: 575.00
Max Obs: 652.00
Parameter Estimates
================================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
--------------------------------------------------------------------------------
const 10.781 0.0723 149.13 0.0000 10.639 10.923
st_louis_fed 0.0945 0.1043 0.9057 0.3653 -0.1102 0.2991
year_1931 -0.3521 0.0853 -4.1285 0.0000 -0.5194 -0.1848
louis_1931 -0.1994 0.1237 -1.6112 0.1074 -0.4422 0.0434
================================================================================
C:\Anaconda\envs\textbook\lib\site-packages\linearmodels\panel\data.py:98: FutureWarning:
is_categorical is deprecated and will be removed in a future version. Use is_categorical_dtype instead
圣路丨易斯联邦储备银行的政策使公司收入减少了 18%( 1 − e − 0.1994 1-e^{-0.1994} 1−e−0.1994)。然而,p 值为 0.1074。结果在 10%的显著性水平下并不具有统计学意义。
from math import exp
1 - exp(dif_in_dif.params.louis_1931 )
0.18076309464004925
有人可能会认为公司之间的差异是一个混杂因素。一个或另一个大公司可能会使结果产生偏差。
这个问题可以通过使用固定效应(FE)或 Within Estimator 来解决。该技术类似于 First-Difference(FD),但数据转换不同。时间去均值过程用于消除未观察到的因素 α i \alpha_i αi。
Y i t = β X i t + α i + ϵ i t Y_{it}=\beta X_{it}+\alpha_i+\epsilon_{it} Yit=βXit+αi+ϵit
然后,我们对每个 i i i在时间 t t t上的变量进行平均:
Y ˉ i = β X ˉ i + α i + ϵ ˉ i \bar{Y}_{i}=\beta \bar{X}_{i}+\alpha_i+\bar{\epsilon}_{i} Yˉi=βXˉi+αi+ϵˉi
然后,我们取差异,未观察到的因素 α i \alpha_i αi消失:
Y i t − Y ˉ i = β ( X i t − X ˉ i ) + ϵ i t − ϵ ˉ i Y_{it}-\bar{Y}_{i}=\beta (X_{it}-\bar{X}_{i})+\epsilon_{it}-\bar{\epsilon}_{i} Yit−Yˉi=β(Xit−Xˉi)+ϵit−ϵˉi
我们可以用更简洁的方式写出上面的方程:
Y ¨ i t = β X ¨ i t + ϵ ¨ i t \ddot{Y}_{it}=\beta \ddot{X}_{it}+\ddot{\epsilon}_{it} Y¨it=βX¨it+ϵ¨it
正如我们之前宣布的,公司是这个面板数据集中的分析单位,计算机会自动使用命令“entity_effects=True”实现公司固定效应(FE)。
我们在双重差分(DID)规范中添加了公司固定效应(FE),结果并没有改变太多。直觉是双重差分(DID)技术已经减轻了内生性问题。
圣路丨易斯联邦政策使公司收入减少了 17%( 1 − e − 0.1862 1-e^{-0.1862} 1−e−0.1862)。结果在 10%的显著水平上是统计上显著的。
firmFE = PanelOLS(Y, df[dd], entity_effects=True)
print(firmFE.fit(cov_type='clustered', cluster_entity=True))
PanelOLS Estimation Summary
====================================================================================
Dep. Variable: log_total_output_value R-squared: 0.2649
Estimator: PanelOLS R-squared (Between): -0.4554
No. Observations: 1227 R-squared (Within): 0.2649
Date: Fri, Nov 06 2020 R-squared (Overall): -0.4266
Time: 21:12:12 Log-likelihood -202.61
Cov. Estimator: Clustered
F-statistic: 34.361
Entities: 938 P-value 0.0000
Avg Obs: 1.3081 Distribution: F(3,286)
Min Obs: 1.0000
Max Obs: 2.0000 F-statistic (robust): 31.245
P-value 0.0000
Time periods: 2 Distribution: F(3,286)
Avg Obs: 613.50
Min Obs: 575.00
Max Obs: 652.00
Parameter Estimates
================================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
--------------------------------------------------------------------------------
const 9.9656 0.4511 22.091 0.0000 9.0777 10.854
st_louis_fed 1.9842 1.0365 1.9144 0.0566 -0.0559 4.0243
year_1931 -0.3666 0.0657 -5.5843 0.0000 -0.4959 -0.2374
louis_1931 -0.1862 0.0982 -1.8965 0.0589 -0.3794 0.0071
================================================================================
F-test for Poolability: 6.8220
P-value: 0.0000
Distribution: F(937,286)
Included effects: Entity
固定效应(FE)可以通过添加虚拟变量手动实现。有不同的固定效应。让我们在双重差分(DID)规范中添加行业固定效应,以排除结果可能受行业特定冲击驱动的可能性。
圣路丨易斯联邦政策使公司收入减少了 14.2%( 1 − e − 0.1533 1-e^{-0.1533} 1−e−0.1533)。结果在 10%的显著水平上是统计上显著的。
为什么不同时添加公司和行业固定效应?这是可能的,也是可取的,但由于多重共线性问题,计算机不会返回任何结果。我们每家公司只有两个观察值(2 年)。如果我们为每家公司添加一个虚拟变量,就像运行一个变量比观察值更多的回归。
在他的论文中,Ziebarth(2013)使用了公司和行业固定效应,这是如何可能的?Ziebarth(2013)使用了 Stata 软件。在多重共线性问题的情况下,Stata 会自动删除一些变量并输出结果。尽管这种做法在经济学顶丨级期刊中很常见,但这并不是“真正”的固定效应。
industryFE = PanelOLS(Y, df[dd + ['industrycode']])
print(industryFE.fit(cov_type='clustered', cluster_entity=True))
PanelOLS Estimation Summary
====================================================================================
Dep. Variable: log_total_output_value R-squared: 0.5498
Estimator: PanelOLS R-squared (Between): 0.5462
No. Observations: 1227 R-squared (Within): 0.3913
Date: Fri, Nov 06 2020 R-squared (Overall): 0.5498
Time: 21:12:12 Log-likelihood -1661.9
Cov. Estimator: Clustered
F-statistic: 29.971
Entities: 938 P-value 0.0000
Avg Obs: 1.3081 Distribution: F(48,1178)
Min Obs: 1.0000
Max Obs: 2.0000 F-statistic (robust): 4.791e+15
P-value 0.0000
Time periods: 2 Distribution: F(48,1178)
Avg Obs: 613.50
Min Obs: 575.00
Max Obs: 652.00
Parameter Estimates
=====================================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
-------------------------------------------------------------------------------------
const 10.391 0.2249 46.201 0.0000 9.9497 10.832
st_louis_fed -0.1740 0.0805 -2.1610 0.0309 -0.3319 -0.0160
year_1931 -0.3163 0.0660 -4.7922 0.0000 -0.4458 -0.1868
louis_1931 -0.1533 0.0916 -1.6741 0.0944 -0.3331 0.0264
industrycode.1005 -0.1966 0.3637 -0.5407 0.5888 -0.9101 0.5169
industrycode.101 0.2349 0.2403 0.9775 0.3285 -0.2366 0.7064
industrycode.1014 -0.1667 1.0812 -0.1542 0.8775 -2.2880 1.9546
industrycode.103 1.5898 0.2938 5.4104 0.0000 1.0133 2.1663
industrycode.104 1.1349 0.2818 4.0280 0.0001 0.5821 1.6877
industrycode.105 0.9660 0.4191 2.3049 0.0213 0.1437 1.7882
industrycode.107 0.9374 0.3073 3.0502 0.0023 0.3344 1.5404
industrycode.110 0.2299 0.3447 0.6671 0.5049 -0.4463 0.9062
industrycode.111 2.8271 0.4097 6.9010 0.0000 2.0233 3.6308
industrycode.112 0.2676 0.4185 0.6394 0.5227 -0.5535 1.0888
industrycode.114 2.7559 0.4623 5.9612 0.0000 1.8489 3.6630
industrycode.116 0.4498 0.4351 1.0337 0.3015 -0.4039 1.3035
industrycode.117 -0.1337 0.5436 -0.2461 0.8057 -1.2002 0.9327
industrycode.118 0.1025 0.2483 0.4127 0.6799 -0.3847 0.5896
industrycode.119 -0.3121 0.2336 -1.3360 0.1818 -0.7705 0.1462
industrycode.1204 -0.0102 0.3031 -0.0338 0.9731 -0.6048 0.5844
industrycode.123 0.2379 0.7093 0.3354 0.7374 -1.1537 1.6295
industrycode.126 1.8847 0.4828 3.9039 0.0001 0.9375 2.8319
industrycode.128 -0.0025 0.5277 -0.0047 0.9963 -1.0377 1.0328
industrycode.1303 2.6410 0.2293 11.519 0.0000 2.1912 3.0908
industrycode.136 0.2537 0.2493 1.0178 0.3090 -0.2354 0.7428
industrycode.1410 -1.4091 0.2967 -4.7496 0.0000 -1.9912 -0.8270
industrycode.1502 1.4523 0.3858 3.7644 0.0002 0.6954 2.2093
industrycode.1604 -0.5652 0.4195 -1.3473 0.1781 -1.3882 0.2579
industrycode.1624 -1.0476 1.0108 -1.0365 0.3002 -3.0307 0.9355
industrycode.1640 -0.8320 0.3613 -2.3030 0.0215 -1.5409 -0.1232
industrycode.1676 0.5830 0.2512 2.3205 0.0205 0.0901 1.0759
industrycode.1677 -0.7025 0.2346 -2.9947 0.0028 -1.1627 -0.2422
industrycode.203 -0.6435 0.2241 -2.8712 0.0042 -1.0832 -0.2038
industrycode.210B 1.7535 0.2293 7.6482 0.0000 1.3037 2.2033
industrycode.216 2.7641 0.3549 7.7888 0.0000 2.0679 3.4604
industrycode.234a 1.6871 0.5410 3.1187 0.0019 0.6258 2.7485
industrycode.265 1.2065 0.4193 2.8774 0.0041 0.3838 2.0292
industrycode.266 -0.3244 0.2736 -1.1857 0.2360 -0.8612 0.2124
industrycode.304 1.2156 0.4982 2.4400 0.0148 0.2382 2.1930
industrycode.314 0.8008 0.2411 3.3211 0.0009 0.3277 1.2740
industrycode.317 -0.1470 0.2750 -0.5347 0.5930 -0.6866 0.3925
industrycode.515 -0.4623 0.2862 -1.6153 0.1065 -1.0238 0.0992
industrycode.518 -0.5243 0.2887 -1.8157 0.0697 -1.0908 0.0422
industrycode.520 -0.2234 0.2731 -0.8179 0.4136 -0.7592 0.3124
industrycode.614 1.8029 0.3945 4.5707 0.0000 1.0290 2.5768
industrycode.622 2.9239 0.2430 12.035 0.0000 2.4473 3.4006
industrycode.633 0.0122 1.5690 0.0078 0.9938 -3.0661 3.0906
industrycode.651 1.9170 0.8690 2.2060 0.0276 0.2121 3.6220
industrycode.652 2.5495 0.2211 11.531 0.0000 2.1158 2.9833
=====================================================================================
仅仅出于练习目的,假设未观察到的因素 α i \alpha_i αi被忽略。这个假设被称为随机效应(RE)。在这种情况下, α i \alpha_i αi将包含在误差项 v i t v_{it} vit中,并可能使结果产生偏见。
Y i t = β X i t + v i t Y_{it}=\beta X_{it}+v_{it} Yit=βXit+vit
v i t = α i + ϵ i t v_{it}= \alpha_i+\epsilon_{it} vit=αi+ϵit
在一个实验中,处理变量与未观察到的因素 α i \alpha_i αi不相关。在这种情况下,随机效应(RE)模型具有产生比固定效应模型更低标准误差的优势。
请注意,如果我们运行简单的随机效应(RE)回归,我们可能错误地得出结论,即圣路丨易斯联邦政策使公司收入增加了 7%。
from linearmodels import RandomEffects
re = RandomEffects(Y, df[['const', 'st_louis_fed']])
print(re.fit(cov_type='clustered', cluster_entity=True))
RandomEffects Estimation Summary
====================================================================================
Dep. Variable: log_total_output_value R-squared: 0.3689
Estimator: RandomEffects R-squared (Between): -0.0001
No. Observations: 1227 R-squared (Within): 0.0025
Date: Fri, Nov 06 2020 R-squared (Overall): -0.0027
Time: 21:12:13 Log-likelihood -1260.9
Cov. Estimator: Clustered
F-statistic: 716.04
Entities: 938 P-value 0.0000
Avg Obs: 1.3081 Distribution: F(1,1225)
Min Obs: 1.0000
Max Obs: 2.0000 F-statistic (robust): 0.5811
P-value 0.4460
Time periods: 2 Distribution: F(1,1225)
Avg Obs: 613.50
Min Obs: 575.00
Max Obs: 652.00
Parameter Estimates
================================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
--------------------------------------------------------------------------------
const 10.518 0.0603 174.36 0.0000 10.399 10.636
st_louis_fed 0.0721 0.0946 0.7623 0.4460 -0.1135 0.2577
================================================================================
练习
假设在非实验设置中,控制组与处理组不同。请解释是否合理使用双重差分(DID)来估计因果效应?在 DID 框架中,你应该修改或添加什么?
假设一项研究声称基于双重差分(DID)方法,联邦储备通过 2008 年的银行纾困避免了大规模的企业倒闭。假设另一项基于回归不连续(RD)的研究声称相反或否认了联邦储备对企业倒闭的影响。你认为哪种是更可信的经验策略,DID 还是 RD 来估计联邦政策的因果影响?请解释你的答案。
在面板数据中,分析单位可以是公司或县,公司级别的结果更可信还是县级别的结果更可信?请解释。
使用 Ziebarth(2013)的数据来估计圣路丨易斯联邦政策对公司收入的影响。具体来说,运行带有随机效应(RE)的双重差分(DID)。解释结果。关于未观察到的因素 α i \alpha_i αi可以推断出什么?
使用 Ziebarth(2013)的数据来估计圣路丨易斯联邦政策对公司收入的影响。具体来说,运行带有公司固定效应(FE)的双重差分(DID),而不使用命令“entity_effects=True”。提示:你必须为每家公司使用虚拟变量。
参考
凯恩斯,约翰梅纳德。 (1936)。《就业、利息和货币的一般理论》。由美丨国 Harcourt,Brace 和 Company 出版,并由美丨国 Polygraphic Company 在纽约印刷。
理查森,加里和威廉特鲁斯特(2009 年)。《大萧条期间货币干预减轻了银行恐慌:来自联邦储备区域边界的准实验证据,1929-1933 年》。《政丨治经济学杂志》117(6):1031-73。
齐巴斯,尼古拉斯 L.(2013 年)。《通过大萧条期间密西西比州的自然实验来识别银行倒闭的影响》。《美丨国经济杂志:宏观经济学》5(1):81-101。