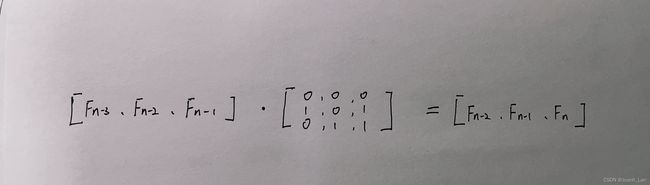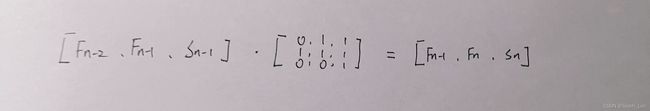矩阵问题入门(矩阵乘法and矩阵快速幂)acm寒假集训日记22/1/15
今天凌晨3点才睡,没想到通过看小说抑制玩游戏,反而看小说的时间更长。
u1s1:那小说太刺激了,晚上看很有感觉,风吹草动我就会猛地看过去(类似茄子说柜子动了,哈哈),真TM(语气词)练胆量!!!..QvQ..
接下来就是正题了!
矩阵乘法
说真的,一开始没有接触过这东西的我是懵逼的!
矩阵乘法的条件:
只有两个矩阵类:A(x*y) and B(y*z)
才可以矩阵相乘,用人话来说:第一个矩阵的列(大小) 等于 第二个矩阵的行(大小)
乘出来的矩阵C(x*z)
矩阵乘的操作:
约定:Axy为第一个人矩阵内的元素A[x,y],Bxy为第二个矩阵内的元素B[x,y].Cxy为第二个矩阵内的元素C[x,y].
C12 = A11*B21 + A12*B22 + A13*B23 +....+A1z*B2z
也就是A矩阵第一行*B矩阵第二列的和
总结:
Cxy = A矩阵第x行*B矩阵第y列的和
由于懒,就借用别人的图片了:
注意事项:
1、当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。
2、矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
矩阵乘法代码:
#include
#include
#include
#include
#define ll long long
using namespace std;
int a[109][109],b[109][109],ans[109][109];
int main()
{
int n,m;
cin>>n>>m;
for(int i = 0;i>a[i][j];
int p;
cin>>p;
for(int i = 0;i>b[i][j];
for(int i = 0;i 矩阵快速幂
矩阵快速幂与正常的快速幂基本上一模一样,只是乘的过程要用矩阵乘法,所以需要封装一个矩阵乘法的函数
void pow(ll p)
{
while(p)
{
if(p&1ll)
mul();
sqr();
p>>=1;
}
}是不是非常的熟悉(简直是一模一样了)
下面是封装函数的写法:(一般会给你很大的数据,所以大部分题目都会要求你mod一下)
void mul()
{
//初始化
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
rem[i][j] = 0;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
for(int k = 1;k<=n;k++)
rem[i][j] += (ans[i][k] % mod* a[k][j] %mod)%mod;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
ans[i][j] = rem[i][j]%mod;
}void sqr()
{
//初始化
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
rem[i][j] = 0;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
for(int k = 1;k<=n;k++)
rem[i][j] += (a[i][k] % mod* a[k][j] %mod)%mod;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
a[i][j] = rem[i][j]%mod;
}还有一个地方需要特别注意:
ans的初始化,“斜向上对角线为1” 当i=j的时候,ans[i][j] = 1;
//初始化
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
{
if(i==j)
ans[i][j] = 1;
//也可以写成ans[i][j] = (i==j)
}完整代码:
#include
#include
#define ll long long
using namespace std;
int n;
const ll mod = 1e9+7;
ll k,ans[109][109],rem[109][109],a[109][109];
void sqr()
{
//初始化
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
rem[i][j] = 0;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
for(int k = 1;k<=n;k++)
rem[i][j] += (a[i][k] % mod* a[k][j] %mod)%mod;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
a[i][j] = rem[i][j]%mod;
}
void mul()
{
//初始化
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
rem[i][j] = 0;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
for(int k = 1;k<=n;k++)
rem[i][j] += (ans[i][k] % mod* a[k][j] %mod)%mod;
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
ans[i][j] = rem[i][j]%mod;
}
void pow(ll p)
{
while(p)
{
if(p&1ll)
mul();
sqr();
p>>=1;
}
}
int main()
{
scanf("%d %lld",&n,&k);
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
scanf("%lld",&a[i][j]);
//初始化
for(int i = 1;i<=n;i++)
for(int j = 1;j<=n;j++)
{
if(i==j)
ans[i][j] = 1;
//也可以写成ans[i][j] = (i==j)
}
pow(k);
for(int i = 1;i<=n;i++)
{
for(int j = 1;j<=n;j++)
{
printf("%lld ",ans[i][j]);
}
printf("\n");
}
} 用矩阵快速幂解决的问题
递推函数 的第N项,前N项和.......
但注意:只能解决"+"的问题(类似斐波那契数:Fn = Fn-1 + Fn-2)
以求Fibonacci 第 n 项为例:
我们可以通过矩阵乘 代替传统的递归写法:
注:有很多种写法,我这样写单纯是因为板子是这个(3*3),你也可以写成【Fn-2,Fn-1】再去找满足题意的矩阵!!!
观察这个式子:
知识储备:矩阵乘 存在结合律
我们求Fibonacci第10项,是不是相当于乘了10-3 = 7次我们构造的矩阵,那我们就可以使用快速幂来优化到log级别
同理 求第n项
n<3 ----->1
n>=3 ----->快速幂(pow(n-3))---->ans[1][3] + ans[2][3] + 2*ans[3][3]
(初始是1 1 2)
代码如下(结合代码更好理解):
#include
#include
#include
#define ll long long
using namespace std;
ll n;
ll mod;
ll k, ans[10][10], rem[10][5], a[10][10];
void sqr()
{
//初始化
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
rem[i][j] = 0;
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
for (int k = 1; k <= 3; k++)
rem[i][j] += (a[i][k] % mod * a[k][j] % mod) % mod;
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
a[i][j] = rem[i][j] % mod;
}
void mul()
{
//初始化
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
rem[i][j] = 0;
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
for (int k = 1; k <= 3; k++)
rem[i][j] += (ans[i][k] % mod * a[k][j] % mod) % mod;
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
ans[i][j] = rem[i][j] % mod;
}
void pow(ll p)
{
while (p)
{
if (p & 1ll)
mul();
sqr();
p >>= 1;
}
}
int main()
{
scanf("%lld %lld", &n, &mod);
if (n < 3)
{
cout << 1 << endl;
return 0;
}
if (n == 3)
{
cout << 2 << endl;
return 0;
}
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
{
if (i == j)
ans[i][j] = 1;
}
a[2][1] = 1;
a[2][3] = 1;
a[3][2] = 1;
a[3][3] = 1;
pow(n - 3);
cout <<(ans[1][3] + ans[2][3] + 2*ans[3][3])%mod ;
} 再来道题吧
Fibonacci 前 n 项和
Sn = Fn-1 + Fn-2 +Sn-1
代码如下:
#include
#include
#include
#define ll long long
using namespace std;
ll n;
ll mod;
ll k, ans[10][10], rem[10][5], a[10][10];
void sqr()
{
//初始化
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
rem[i][j] = 0;
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
for (int k = 1; k <= 3; k++)
rem[i][j] += (a[i][k] % mod * a[k][j] % mod) % mod;
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
a[i][j] = rem[i][j] % mod;
}
void mul()
{
//初始化
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
rem[i][j] = 0;
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
for (int k = 1; k <= 3; k++)
rem[i][j] += (ans[i][k] % mod * a[k][j] % mod) % mod;
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
ans[i][j] = rem[i][j] % mod;
}
void pow(ll p)
{
while (p)
{
if (p & 1ll)
mul();
sqr();
p >>= 1;
}
}
int main()
{
scanf("%lld %lld", &n, &mod);
if(n==1)
{
cout<<1< 最后,感谢您的阅读!!!