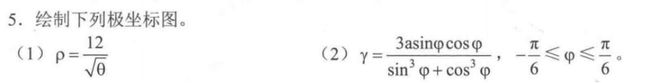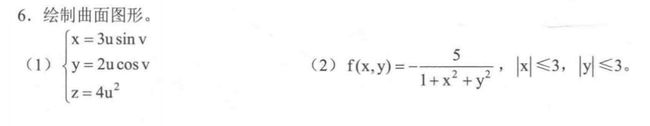MATLAB程序设计教程 第3版 第四章实验指导、思考练习答案（个人版）

注：本系列文章仅仅用于交流学习，杜绝作业抄袭

第一章：MATLAB程序设计教程 第3版 第一章实验指导、思考练习答案（个人版）-CSDN博客

第二章：MATLAB程序设计教程 第3版 第二章实验指导、思考练习答案（个人版）-CSDN博客

第三章：MATLAB程序设计教程 第3版 第三章实验指导、思考练习答案（个人版）-CSDN博客

第四章：MATLAB程序设计教程 第3版 第四章实验指导、思考练习答案（个人版）-CSDN博客

第五章：MATLAB程序设计教程 第3版 第五章实验指导、思考练习答案（个人版）-CSDN博客

第六章：MATLAB程序设计教程 第3版 第六章实验指导、思考练习答案（个人版）-CSDN博客

实验指导：

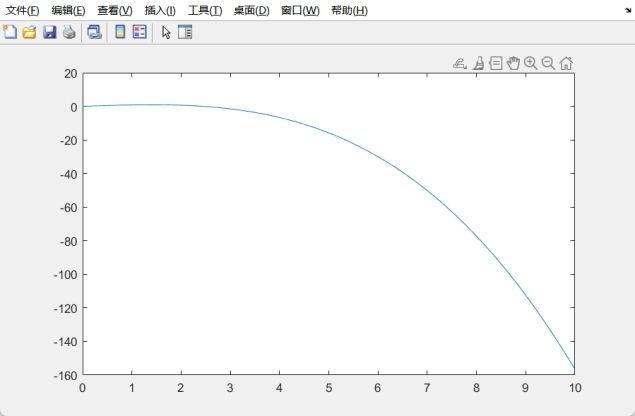
x=0:1/1000:10;

y=x-x.^3./6;

plot(x,y)

ezplot(@(x, y) x.^2 + 2*y.^2 - 64, [-20, 20, -20, 20]); % 范围可能需要根据方程进行调整

title('x^2 + 2*y^2 = 64 的图形');

xlabel('X 轴');

ylabel('Y 轴');

 x=-pi:pi/10:pi;

y=1./(1+exp(-1*x));

subplot(2,2,1);bar(x,y,'g');

title('bar(x,y,"g")');axis([0,7,-2,2]);

subplot(2,2,2);stairs(x,y,'b');

title('stairs(x,y,"b")');axis([0,7,-2,2])

subplot(2,2,3);stem(x,y,'k');

title('stem(x,y,"k")');axis([0,7,-2,2]);

 

subplot(2,2,4);semilogy(x, y, 'g'); 

title('semilogy(x, y, "g")');axis([0,7,-2,2]);

%subplot(2,2,5);semilogx(x, y, 'b'); 

%title('semilogx(x, y, "b")');axis([0,7,-2,2]);

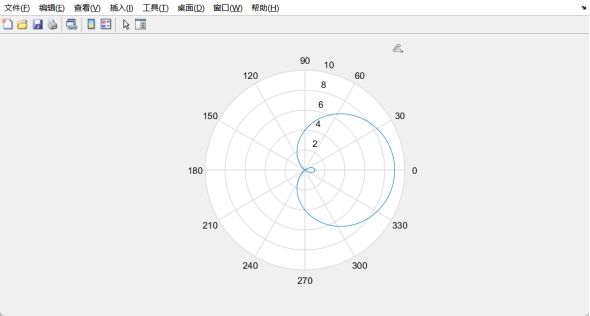
theta=0:0.01:2*pi;

rho=5.*cos(theta)+4;

polar(theta,rho)

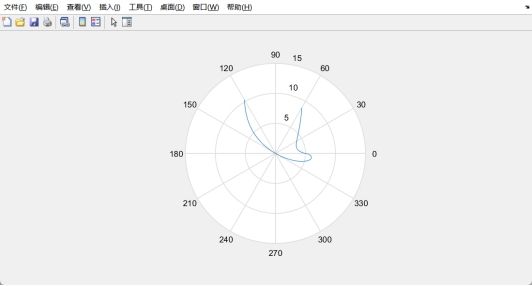
theta=-pi/3:0.01:pi/3;

rho=(5*sin(theta).^sin(theta))./cos(theta);

polar(theta,rho)

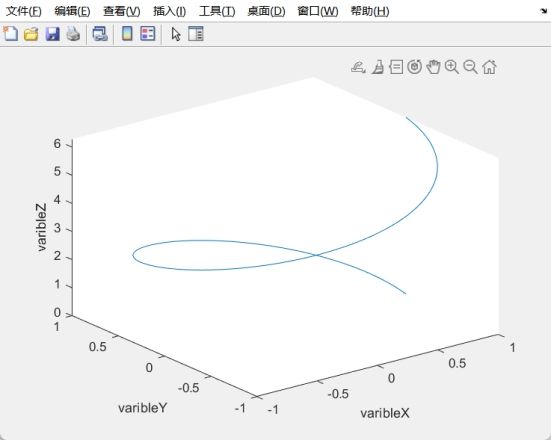
t = 0:pi/100:2*pi;

x = exp(0).^(-t/20).*cos(t);

y = exp(0).^(-t/20).*sin(t);

z = t;

plot3(x,y,z);

 

xlabel('varibleX');

ylabel('varibleY');

zlabel('varibleZ');

x = -5:0.01:5;

y = -5:0.01:5;

[X, Y] = meshgrid(x, y);

Z = ones(size(X));

surf(X, Y, Z);

shading interp;

 

xlabel('varibleX');

ylabel('varibleY');

zlabel('varibleZ');

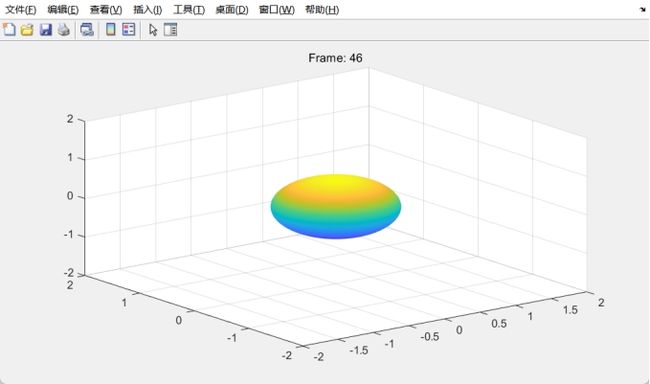
% 创建一个时间向量

t = linspace(0, 4*pi, 100);

 

% 创建一个新的图形窗口

figure;

 

for i = 1:length(t)

% 计算球体的半径，这里使用正弦函数使得半径随时间变化

radius = 1 + 0.5*sin(t(i));

% 创建球体的坐标

[x, y, z] = sphere(50); % 创建球体坐标数据

x = x * radius; % 根据半径调整 x 坐标

y = y * radius; % 根据半径调整 y 坐标

z = z * radius; % 根据半径调整 z 坐标

% 绘制球体并设置一些属性

surf(x, y, z, 'EdgeColor', 'none'); % 绘制球体

axis([-2 2 -2 2 -2 2]); % 设置坐标轴范围

title(sprintf('Frame: %d', i)); % 显示当前帧数

drawnow; % 更新绘图窗口

% 添加适当的延时，控制动画播放速度

pause(0.1);

% 在绘制下一帧前清除图形

clf;

end

思考练习

一、填空题

plot(x,y) title(‘正弦波’) xlable(‘时间’) ylable(‘幅度’)

3

hold on axis([-3 3 -5 20])

单位圆

五个同心圆，半径依次为1,3,5,7,9

二、问答题

1、使用plot函数：使用多次plot函数调用来绘制多条曲线。每次调用plot函数时，指定不同的数据点作为曲线的 x 和 y 值。例如：

x1 = 0:0.1:2*pi;
y1 = sin(x1);
x2 = 0:0.1:2*pi;
y2 = cos(x2);
plot(x1, y1, x2, y2)

2、使用hold on和hold off：使用hold on命令来保持当前的坐标轴，并允许多次绘制，然后使用hold off命令来恢复默认行为。例如：

x = 0:0.1:2*pi;
y1 = sin(x);
y2 = cos(x);
plot(x, y1)
hold on
plot(x, y2)
hold off

3、使用数组方式：将要绘制的曲线数据存储在一个矩阵或向量中，然后使用plot函数一次性绘制所有的曲线。每一列或每一个元素表示一条曲线的数据。例如：

x = 0:0.1:2*pi;
y = [sin(x); cos(x); tan(x)];
plot(x, y)

x=0:0.01:10;
y=1/(2*pi)*exp(-0.5.*x.*x);
plot(x,y)

t=0:0.1:2*pi;
x=t.*sin(t);
y=t.*cos(t);
plot(x,y);

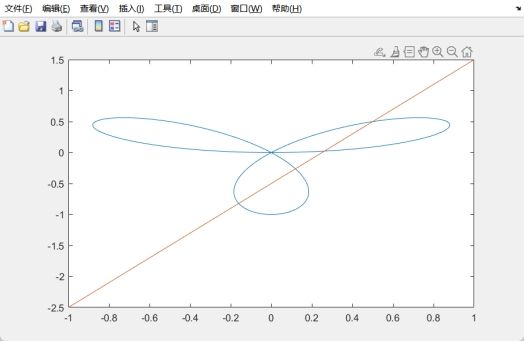
t=0:0.01:2*pi;

x=sin(3*t).*cos(t);

y=sin(3*t).*sin(t);

plot(x,y);

hold on;

x=-1:0.01:1;

y=2*x-0.5;

plot(x,y);

hold off

x=linspace(0.01,0.02,50);

y=sin(1./x);

subplot(2,1,1),plot(x,y);

subplot(2,1,2),fplot(@(x)sin(1./x),[0.01,0.02]);

t = 0:pi/100:2*pi;

r = 12./sqrt(t);

polar(t,r);

a = 3;

t = -pi/6:pi/100:pi/6;

r = 3*a*sin(t).*cos(t)./(sin(t).^3+cos(t).^3);

polar(t,r);

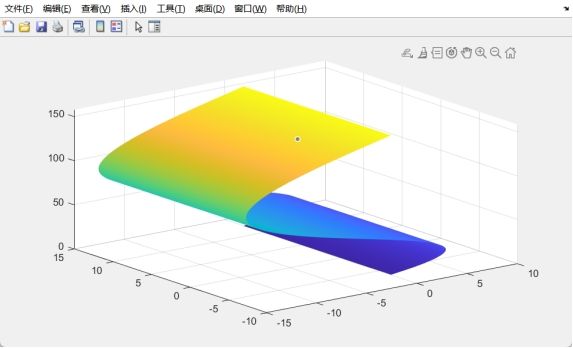
u = 0:pi/100:2*pi;

v= 0:pi/100:2*pi;

x = 3 * u.*sin(v);

y = 2*u.*cos(v);

[U,V] = meshgrid(u,v);

z = 4*U.^2;

surf(x,y,z);shading interp;

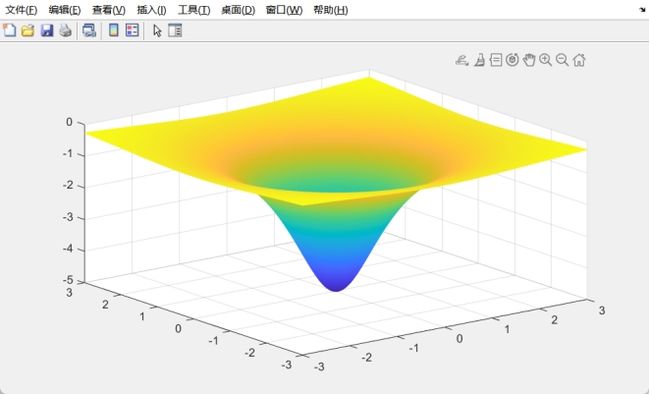
x = -3:0.01:3;

y = -3:0.01:3;

 

[X,Y] = meshgrid(x,y);

z = -5./(1+X.^2+Y.^2);

mesh(x,y,z);shading interp;