【刷题之路Ⅲ】LeetCode 827. 最大人工岛

一、题目描述

二、解题思路及代码

读完题目我们会发现，这道题正来做其实是很难的，那我们就反着做。

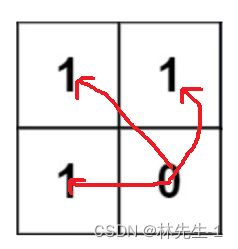
我们可以将思路转化为由数字是0的格子出发，统计与它相邻的岛屿的面积，依次遍历完所有的0格子，就能得到最大的面积了：

统计面积的操作使用bfs来做，但是如果直接这样做我们会发现，存在许多的重复计算，就比如下面这个例子：

右上角和左下角的两个0的相邻岛屿其实是同一个，如果这种重复相邻的岛屿很多的话，很可能就会超时，

我这里已经帮大家试验过了，直接计算的话，是会超时的：

代码：

// 开始解题：
// 方法——bfs(暴力)
class Solution {
public:
    // 向量数组
    int dx[4] = { -1, 1, 0, 0 }, dy[4] = { 0, 0, -1, 1 };
    int bfs(vector>& grid, int row, int col) {
        int n = grid.size();
        vector> vis(n, vector(n, false));
        vis[row][col] = true;
        int ret = 1;
        queue> q;
        q.push({ row, col });
        while (!q.empty()) {
            int a = q.front().first, b = q.front().second;
            q.pop();
            for (int k = 0; k < 4; k++) {
                int x = a + dx[k], y = b + dy[k];
                if (x >= 0 && x < n && y >= 0 && y < n && !vis[x][y] && grid[x][y] == 1) {
                    ret++;
                    vis[x][y] = true;
                    q.push({ x, y });
                }
            }
        }
        return ret;
    }
    int largestIsland(vector>& grid) {
        int n = grid.size();
        int ret = 1;
        int flag = 0; // 标记是否出现了数字0
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 0) {
                    flag = 1;
                    for (int k = 0; k < 4; k++) {
                        int x = i + dx[k], y = j + dy[k];
                        if (x >= 0 && x < n && y >= 0 && y < n && grid[x][y] == 1) {
                            ret = max(ret, bfs(grid, i, j));
                            break; // 因为这里是直接计算的，所以只需要计算一次即可，其他的全是重复计算
                        }
                    }
                }
            }
        }
        if (flag) {
            return ret;
        }
        return n * n; // 没有0就直接返回整个矩阵的面积
    }
};

运行结果：

那我们该怎么解决这个重复计算的问题呢？

我们可以在bfs的过程中对每个岛屿进行编号(其实是对一个岛屿的每个格子都编号)，然后用哈希表来记录每个岛屿编号对应的面积。

开始时先对每个岛屿进行编号并统计面积，然后在枚举数字为0的格子，计算与它相邻(上下左右四个方向相邻)的岛屿的面积。

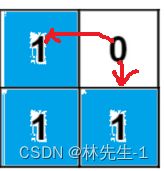
因为我们现在不是直接计算了，而是直接加上岛屿的面积，所以还有可能会出现重复计算一个岛屿的情况：

例如：

我们在枚举0的上下左右四方方向时，如上图左边和下边相邻的岛屿是同一个，这就重复计算了，所以我们还得用一个哈希表来记录每个0格子累加过的岛屿编号，从而避免重复计算。

代码：

// 开始解题：
// 方法——标记岛屿 + bfs
class Solution {
public:
    int area = 0; // 统计某个岛屿的面积
    int number = 1; // 岛屿的编号
    int n = 0;
    int dx[4] = { -1, 1, 0, 0 }, dy[4] = { 0, 0, -1, 1 };
    int vis[510][510]; // 标记每个岛屿是否被访问过, 访问过就加上编号，表示gird[i][j格子]所在的岛屿的标号为vis[i][j]
    unordered_map islan; // 存储每个编号对应的岛的面积

    void bfs(vector>& grid, int row, int col) {
        vis[row][col] = number;
        queue> q;
        q.push({ row, col});
        while (!q.empty()) {
            int a = q.front().first;
            int b = q.front().second;
            q.pop();
            for (int k = 0; k < 4; k++) {
                int x = a + dx[k], y = b + dy[k];
                if (x >= 0 && x < n && y >= 0 && y < n && !vis[x][y] && grid[x][y] == 1) {
                    area++;
                    vis[x][y] = number;
                    q.push({ x, y});
                }
            }
        }
        islan[number] = area;
    }

    int largestIsland(vector>& grid) {
        n = grid.size();
        // 先将每个岛屿标记
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1 && !vis[i][j]) {
                    area = 1;
                    bfs(grid, i, j);
                    number++; // 计算完一个岛屿，umber++
                }
            }
        }

        // 再计算最大面积
        int ret = 0;
        int flag = 0; // 标记是否找到0
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++){
                if (grid[i][j] == 0) {
                    flag = 1;
                    unordered_set hash;
                    int temp_area = 1; // 面积从1开始，表示0格子的面积
                    for (int k = 0; k < 4; k++) {
                        int x = i + dx[k], y = j + dy[k];
                        if (x >= 0 && x < n && y >= 0 && y < n && grid[x][y] == 1) {
                            if (!hash.count(vis[x][y])) {
                                temp_area += islan[vis[x][y]];
                                hash.insert(vis[x][y]);
                            }

                        }
                    }
                    ret = max(ret, temp_area);
                }
            }
        }
        if (flag) {
            return ret;
        }
        return n * n; // 如果没有发现0，就直接返回整个矩阵的面积
    }
};

运行结果：