代码随想录刷题笔记-Day14

 1. 对称二叉树

101. 对称二叉树https://leetcode.cn/problems/symmetric-tree/给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

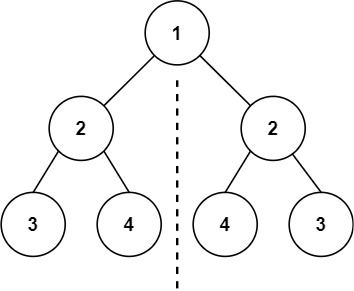
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

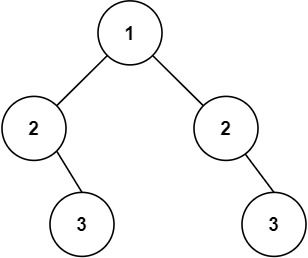
输入：root = [1,2,2,null,3,null,3]
输出：false

解题思路

判断一个二叉树是否对称，也就是需要同时遍历左右子树，并且比较对称位置的值。

先看以递归的办法进行遍历的时候：

首先要确定递归终止条件。当left当前遍历的节点和right当前遍历的节点都为null的时候就是true。只有一个为null的时候就是false，当都不为true的时候，如果值不一样也为false。

第二个是递归的传参，迭代的传参就是left和right的下一个节点。

最后要确定的是返回值，把左右子树的返回值做一个and操作。

以迭代的办法进行遍历的时候：

左右都使用一个栈，

左右子树都需要进行迭代遍历，为了解决不为满二叉树的时候无法感知到取出的节点位于层次的具体位置，我们需要把整个二叉树当作满二叉树。也就是说不论节点的左右子节点是否为null都进行入栈。当取出来为null的时候就跳过。

当取出来的都为null的时候，continue；当只有一个为null或者val不一样的时候返回false；当val一样的时候，就把子节点进行入栈。

使用一个双端队列，两端就是两个栈。

代码

递归法

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null)
            return true;
        return compare(root.left, root.right);
    }

    public boolean compare(TreeNode left, TreeNode right) {
        if (left == null && right == null)
            return true;
        else if ((left != null && right == null) || (left == null && right != null))
            return false;
        else if (left.val != right.val)
            return false;
        return compare(left.left, right.right) && compare(left.right, right.left);
    }
}

迭代法

   public boolean isSymmetric(TreeNode root) {
        Deque queue = new LinkedList<>();
        queue.addFirst(root.left);
        queue.addLast(root.right);
        while (!queue.isEmpty()) {
            TreeNode left = queue.pollFirst();
            TreeNode right = queue.pollLast();
            if (left == null && right == null)
                continue;
            else if (left == null || right == null || left.val != right.val)
                return false;
            queue.addFirst(left.left);
            queue.addLast(right.right);
            queue.addFirst(left.right);
            queue.addLast(right.left);
        }

        return true;
    }

2. 二叉树的最大深度

104. 二叉树的最大深度https://leetcode.cn/problems/maximum-depth-of-binary-tree/

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

解题思路

最大深度就是二叉树的层高。

第一个想法就是层级遍历的次数。也就是迭代法。

然后又考虑递归实现的可能性：

返回值为当前节点的层高。

终止递归的情况是当前节点为null，返回0；

每一层的处理就是返回左右子树的最高层高的最大值+1；

代码

递归

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null)
            return 0;
        return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
    }
}

迭代

class Solution {
    public int maxDepth(TreeNode root) {
        Deque queue = new LinkedList<>();
        int high = 0;
        if (root == null)
            return high;
        queue.add(root);
        while (!queue.isEmpty()) {
            int len = queue.size();
            while (len > 0) {
                TreeNode node = queue.poll();
                if (node.left != null)
                    queue.add(node.left);
                if (node.right != null)
                    queue.add(node.right);
                len--;
            }

            high++;
        }
        return high;
    }
}

3. 二叉树的最小深度

111. 二叉树的最小深度https://leetcode.cn/problems/minimum-depth-of-binary-tree/

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

解题思路

首先是递归法的思考：

结束条件是左右节点都为null，返回1。所以加入递归前先判断是否为null。

返回值是子树的最小高度+1。

迭代法：

在层次遍历记录深度的同时，当一个节点没有子节点的时候，说明这个节点为叶子节点，直接返回当前深度；

代码

递归

class Solution {
	public int minDepth(TreeNode root) {
		if (root == null)
			return 0;
		if (root.left == null && root.right != null) {
			return 1 + minDepth(root.right);
		}
		if (root.left != null && root.right == null) {
			return 1 + minDepth(root.left);
		}
		return Math.min(minDepth(root.left), minDepth(root.right)) + 1;
	}
}

迭代法

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null)
            return 0;
        Deque queue = new LinkedList<>();
        int deepth = 0;
        queue.add(root);
        while (!queue.isEmpty()) {
            int len = queue.size();
            while (len > 0) {
                TreeNode node = queue.poll();
                if (node.left == null && node.right == null) {
                    return deepth + 1;
                }
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
                len--;
            }
            deepth++;
        }
        return deepth;

    }
}