Phil的课堂笔记之排序

排序总结

今天讲了排序算法，在这里做一下总结

稳定排序

• 快速排序、希尔排序、堆排序、直接选择排序不是稳定的排序算法。
• 基数排序、冒泡排序、直接插入排序、折半插入排序、归并排序是稳定的排序算法。
  时间复杂度
  
  

目录

1. 冒泡排序
2. 快速排序
3. 归并排序

1.所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。排序算法，就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视，尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。

2.排序(Sorting) 是 计算机程序设计中的一种重要操作，它的功能是将一个 数据元素（或记录）的任意序列，重新排列成一个关键字有序的序列。

3.稳定度（稳定性）

一个 排序算法是 稳定的，就是当有两个相等记录的关键字 和 ，且在原本的列表中 出现在 之前，在排序过的列表中 也将会是在 之前。

当相等的元素是无法分辨的， 比如像是整数，稳定度并不是一个问题。然而，假设以下的数对将要以他们的第一个数字来 排序。

1.0 冒泡排序

2.0 快速排序

P1177 【模板】快速排序
大家看完以后可以去水一下这个题，虽然sort可以一遍过

快速排序是基于分治的思想，
最差时间复杂度是O(N^2)
它的平均时间复杂度为O(NlogN)
先从比较的数组中挑出一个基准数，然后用两个指针，
指针i指向数组开头，另一个指针j指向数组结尾，
通过一趟排序将数组分成两个部分,其中一个部分都比关键字小,另一个部分都比 关键字 大,然后再分别对这两部分进行这种操作,最后就可以达到全部有序
原图：@洛谷用户:跪下叫哥------ 原网址

通常我们取待排序部分的第一个值为关键字
我们能不能把步骤想的更具体一点,怎么样做才能把数分成这样的两个部分?





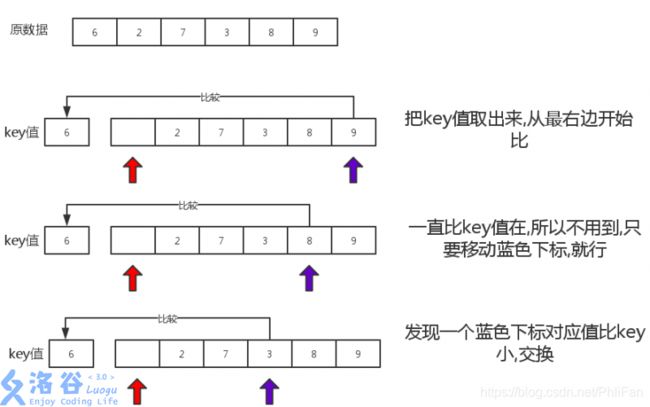
上面的图片解释了一趟快速排序的原理,如果你有足够的想想象力,可以把红色,蓝色下标想象成两个机器人,它们不停的移动去判断值,一但符合条件,就把箱子里的值仍给另一个机器人,自己停止,另一个机器人又开始工作,这样的不停往返的下去,就可以把数分成两个部分了。

快速排序之所比较快，因为相比冒泡排序，每次交换是跳跃式的。每次排序的时候设置一个基准点，将小于等于基准点的数全部放到基准点的左边，将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换，交换的距离就大的多了。因此总的比较和交换次数就少了，速度自然就提高了。当然在最坏的情况下，仍可能是相邻的两个数进行了交换。
因此快速排序的最差时间复杂度和冒泡排序是一样的都是O(N^2)，它的平均时间复杂度为O(NlogN)。

板子代码如下

0.1~基准数为中间数

#include
#include
#include
#include
#include
using namespace std;
int n,a[1000005];
void qsort(int l, int r){
  if(l >= r) return;
  int i = l, j = r, tmp = a[(l + r) / 2];
  while(1){
    while(a[i] < tmp && i < r) i++;
    while(a[j] > tmp && j > l) j--;//边界:1 2 4,j--保证不越界
    //也可能是i
    //这个之后，可能是i == j, 3(i) tmp 6(j)
    //也可能是i>j 3(i) 6(j) 
    if(i <= j){
      swap(a[i], a[j]);
      i++,j--;
    }
    if(i>j) break;
  }
  qsort(l, j);
  qsort(i,r);
}
int main(){
  scanf("%d",&n);
  for(int i = 1; i <= n; i++) scanf("%d",&a[i]);
  qsort(1,n);
  for(int i = 1; i <= n; i++)printf("%d ",a[i]); printf("\n");
  return 0;
}

0.2基准数为最前或最后数

代码作者：相思明月楼

#include 
int a[101],n;//定义全局变量，这两个变量需要在子函数中使用
void quicksort(int left, int right) {
	int i, j, t, temp;
	if(left > right)
		return;
    temp = a[left]; //temp中存的就是基准数
    i = left;
    j = right;
    while(i != j) { //顺序很重要，要先从右边开始找
    	while(a[j] >= temp && i < j)
    		j--;
    	while(a[i] <= temp && i < j)//再找右边的
    		i++;       
    	if(i < j)//交换两个数在数组中的位置
    	{
    		t = a[i];
    		a[i] = a[j];
    		a[j] = t;
    	}
    }
    //最终将基准数归位
    a[left] = a[i];
    a[i] = temp;
    quicksort(left, i-1);//继续处理左边的，这里是一个递归的过程
    quicksort(i+1, right);//继续处理右边的 ，这里是一个递归的过程
}
int main() {
	int i;
    //读入数据
	scanf("%d", &n);
	for(i = 1; i <= n; i++)
		scanf("%d", &a[i]);
    quicksort(1, n); //快速排序调用
    //输出排序后的结果
    for(i = 1; i < n; i++)
    	printf("%d ", a[i]);
    printf("%d\n", a[n]);
    return 0;
}

3.0 归并排序

原文链接:CSDN博主「杨江涛-Cena」

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
  算法思路，将大问题化解为一个个小问题，通过解决小问题来解决大问题

3.1 归并模版代码（老师

#include 
int a[101],n;//定义全局变量，这两个变量需要在子函数中使用
void quicksort(int left, int right) {
	int i, j, t, temp;
	if(left > right)
		return;
    temp = a[left]; //temp中存的就是基准数
    i = left;
    j = right;
    while(i != j) { //顺序很重要，要先从右边开始找
    	while(a[j] >= temp && i < j)
    		j--;
    	while(a[i] <= temp && i < j)//再找右边的
    		i++;       
    	if(i < j)//交换两个数在数组中的位置
    	{
    		t = a[i];
    		a[i] = a[j];
    		a[j] = t;
    	}
    }
    //最终将基准数归位
    a[left] = a[i];
    a[i] = temp;
    quicksort(left, i-1);//继续处理左边的，这里是一个递归的过程
    quicksort(i+1, right);//继续处理右边的 ，这里是一个递归的过程
}
int main() {
	int i;
    //读入数据
	scanf("%d", &n);
	for(i = 1; i <= n; i++)
		scanf("%d", &a[i]);
    quicksort(1, n); //快速排序调用
    //输出排序后的结果
    for(i = 1; i < n; i++)
    	printf("%d ", a[i]);
    printf("%d\n", a[n]);
    return 0;
}

板子题——逆序对

洛谷-P1908 逆序对

本题是一个用归并排序很好想答案的一个题
首先我们假设两个有序序列
序列1：5 7 8 9
序列2：1 3 4 6
那么，按照刚才归并排序的思路，就应该用两个序列中的第一个比大小，踢出小的，存到新数组当中，然后继续比大小
所以我们现在需要思考一个问题：逆序对在归并排序中的本质是什么？

我们可以发现：如果两数为逆序对，那么，这两个数必定处于两个序列中，并且大数在前面那个序列中，
就拿我们举的序列来说，在一序列中，5 在序列1中，1在序列2中，在归并中，1比5先进入新数组，（1比5小），那么5 1就为逆序对
所以我们就可以直接在归并过程中加一个计数用的变量就可以完美解决问题咯！
但问题来了：怎么加呢？？？

下面我们具体来看怎样操作这个计数变量

int cnt；

序列1：5 7 8 9
序列2：1 3 4 6

序列2中，1 is smaller than 5, so 1 is first put into the sequence，that is to say , 1 is smaller than any elements in group 1;so we should add the mount of all element that are left now;
so here is the key;

cnt +=mid-i+1;// i 是序列1 当前的位置，mid是中间数

注意！：本题计数需要用 long long ，用int 会爆；

实现程序奉上！

#include
#include
using namespace std;
long long cnt;
int n,a[500005],c[500005];

void merge(int b,int e)//归并排序 
{
    if(b==e) return;
    int mid=(b+e)/2;int k=b;int i=b,j=mid+1;//把c数组分成两部分 
    merge(b,mid);merge(mid+1,e);
    
    while(i <= mid && j <= e){
    	if		(a[i] <= a[j])	c[k++]=a[i++];
    	else    {c[k++] = a[j++],cnt+=mid-i+1;} 
	}
	while(i<= mid)	c[k++]=a[i++];
	while(j<= e)	c[k++]=a[j++];
	for(int l =b ;l <= e;l++)
		a[l]=c[l];
}

int main()
{
    scanf("%d",&n); 
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]); 
    merge(1,n);
    printf("%lld",cnt);
    return 0;
}