FSP语言学习（一）：对单个process建模

目录

一、什么是正式建模语言

1. 正式建模语言是进程代数

2. 为什么要使用正式建模语言

二、Finite State Processes

1. FSP的基本概念

2. FSP—the action prefix

3. FSP—choice

4. FSP—non-deterministic choice

5. FSP—indexed processes

6. FSP—constants and ranges

7. FSP—Process Parameters

8. FSP—guarded actions

9. FSP—the STOP process

10. FSP—Process Alphabets

---

一、什么是正式建模语言

1. 正式建模语言是进程代数

正式建模，像有Finite State Processes (FSP) 是一种建模语言，它基于Communicating Sequential Processes (CSP) 和 Calculus of Communicating Systems (CCS)。在这些语言中操作和推理表达式的规则称为进程代数（有时也称为进程演算）。

2. 为什么要使用正式建模语言

正式建模语言，例如FSP，具有定义良好的语法和语义，与编程语言非常相似。事实上，FSP具有比大多数编程语言更严格的语义定义。

首先，正式的建模语言有两个优点：

• 它使我们的思维更加严谨。
• 它为我们提供了分析我们的模型所需的严谨性。建模语言将模型与问题的物理环境相比较并以一种精确的方式进行权衡。

如果不使用正式建模语言，那我们对模型的描述就像再给我们的代码写注释一样，充斥着歧义和不完整的问题。

二、Finite State Processes

1. FSP的基本概念

一个进程是一个顺序程序的执行。进程在任何时间点的状态由程序员声明的显性变量的值和隐性变量组成，如程序计数器和数据/地址寄存器的内容。随着进程的执行，它通过执行语句来改变其状态。

每个语句由一个或多个原子动作（“alphabet”）的序列组成，这些原子动作会使状态发生不可分割的变化。原子动作的例子是加载和存储寄存器的不间断的机器指令。一个更抽象的过程模型，忽略了状态表示和机器指令的细节，只是把一个过程看作是有一个被不可分割的或原子性的动作修改的状态。每个动作都会导致从当前状态到下一个状态的转换。允许动作发生的顺序由过渡图决定，过渡图是程序的一个抽象表示。换句话说，我们可以将进程建模为有限状态机。

下图描述了一个有开和关动作的电灯开关的状态机。

我们使用以下的图表惯例。初始状态总是被编号为0，过渡总是按顺时针方向绘制。因此在图2.1中，开导致从状态（0）到状态（1）的转换，关导致从状态（1）到状态（0）的转换。这种形式的状态机描述被称为标记过渡系统（Labeled Transition System，LTS），因为过渡是用动作名称标记的。这种形式的图可以在LTS分析工具LTSA中显示。尽管这个过程的表示是有限的，但所描述的行为不一定是有限的。例如，上图的状态机允许以下的动作序列：

on → off → on → off → on → off → ...

状态机描述的图形形式对于简单的进程来说是非常好的；然而，对于大量的状态和转换来说，它变得难以管理（和难以阅读）。因此，我们引入了一个简单的代数符号，称为FSP（有限状态过程）来描述过程模型。每个FSP描述都有一个相应的状态机（LTS）描述。这一篇博客，我们将介绍FSP所提供的动作前缀和选择操作符。

总结一下：

FSP允许描述一个或多个独立运行的进程，但它们可能在不同点上同步。FSP中的每个流程模型都由一组可能发生在该流程中的原子动作（“alphabet”）和一个定义组成，该定义规定了系统中原子动作的合法序列。

每个进程，以及并发进程如何同步，都使用一组代数运算符来描述。

2. FSP—the action prefix

x -> P

x是一个动作，P是一个过程。上面的表达式描述了一个Process，它最初参与到动作x中，然后像P那样行动。

动作前缀操作符""的左边总是有一个动作，右边是一个进程。在FSP中，以小写字母开头的标识符表示动作，以大写字母开头的标识符表示进程。下面的例子说明了一个过程，它参与了一次行动，然后停止。

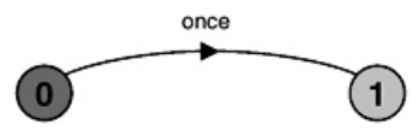
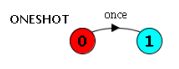
ONESHOT = (once->STOP).

下图说明了ONESHOT的等效LTS状态机描述。它表明FSP中的动作前缀描述了相应状态机描述中的一个转换。STOP是一个特殊的预定义进程，它不参与任何进一步的行动，这在图中很清楚。进程的定义以". "结束。

重复性行为在FSP中是用递归来描述的。下面的FSP过程描述了上图的灯光开关。

SWITCH = OFF,
OFF    = (on ->ON),
ON     = (off->OFF).

正如", "分隔符所示，ON和OFF的进程定义是SWITCH定义的一部分和局部。应该注意的是，这些局部进程定义与图中的状态相对应。OFF定义了状态（0），ON定义了状态（1）。一个更简洁的SWITCH定义可以通过在OFF的定义中替换ON的定义来实现。

SWITCH = OFF,
OFF    = (on ->(off->OFF)).

最后，用SWITCH代替OFF，因为它们被定义为等价的，并去掉内部的括号，我们得到了：

SWITCH = (on->off->SWITCH).

SWITCH的这三个定义产生了相同的状态机。这些定义也可以用LTSA动画器制作成动画，以产生一系列的动作。下图显示了LTSA动画器窗口的屏幕截图。

 动画师让用户控制一个模型向其环境提供的动作。那些可以被选择执行的动作被打上了勾。在图中，左边显示的前一连串的动作使SWITCH处于一个只有on动作才能发生的状态。我们把一个流程（或一组流程）的执行所产生的动作序列称为跟踪。

我们再来学习一个交通控制灯的例子：

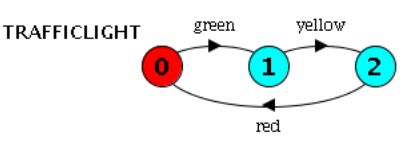
TRAFFIC_LIGHT = (green -> yellow -> red-> TRAFFIC_LIGHT).

上面这个表达式等同于（把每个状态都写成一个进程）：

TRAFFIC_LIGHT = GREEN ,
GREEN = (green -> YELLOW),
YELLOW = (yellow -> RED),
RED = (red -> GREEN).

一般来说，进程有许多可能的执行轨迹。然而，TRAFFICLIGHT的唯一可能的执行轨迹是。

red → orange → green → orange → red → orange → green ...

为了让一个流程能够描述不止一个执行轨迹，我们引入了选择操作符。

3. FSP—choice

choice是用于描述可执行多个可能操作序列的流程。

(x -> P | y -> Q)

上面这个表达式描述了一个Process，如果它第一个动作选择了x，那么随后的行为遵循流程P；如果它第一个动作选择了y，那么它随后的行为遵循流程Q。

下面的例子描述了一台饮料分配机，如果按红色按钮，就会分配热咖啡，如果按蓝色按钮，就会分配冰茶。（注意FSP语言要有良好的空格）

DRINKS = (red->coffee->DRINKS
         |blue->tea->DRINKS
         ).

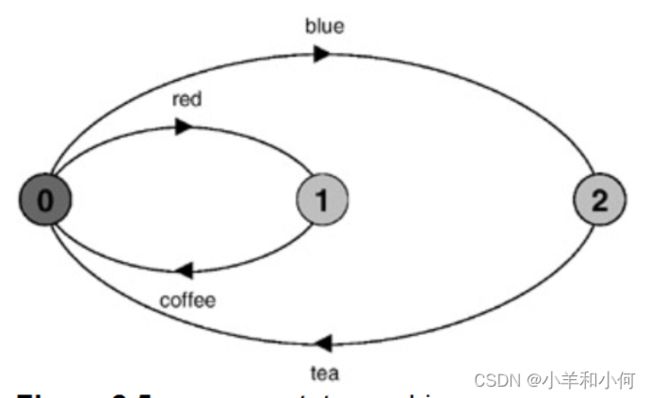
下图描述了饮料分配器的图形状态机描述。选择被表示为具有一个以上的出站过渡的状态。

初始状态（0）有两个可能的传出转换，分别标为红色和蓝色。谁或什么来选择执行哪个动作？在这个例子中，环境做出了选择——有人按了一个按钮。

除了环境做出选择，选择也可能是在一个过程内部做出的。在这一点上，我们可能还会质疑输入和输出动作之间是否有区别。事实上，在我们使用的模型中，输入动作和输出动作之间没有语义上的区别。然而，输入动作通常是通过构成提供给环境的选择的一部分来区分的，而输出则不提供选择。在这个例子中，红色和蓝色是输入动作，咖啡和茶是输出动作。DRINKS的可能痕迹包括。

red → coffee → red → coffee → red → coffee......
blue → tea → blue → tea → blue → tea......
blue → tea → red → coffee → blue → tea → blue → tea......

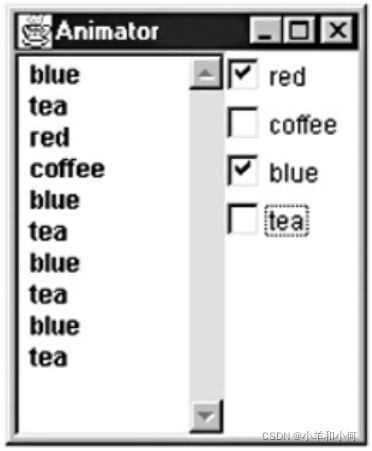
如前所述，LTSA动画师可以用来对模型进行动画处理并产生跟踪，如下图所示。在这种情况下，红色和蓝色的动作都打了勾，因为这两个动作都是提供给人们选择的。

一个状态可能有两个以上的输出转换；因此选择运算符"|"可以表达两个以上的行动选择。例如，下面的过程描述了一台有四个彩色按钮的机器，其中只有一个能产生输出。

FAULTY = (red ->FAULTY
         |blue ->FAULTY
         |green->FAULTY
         |yellow->candy->FAULTY
         ).

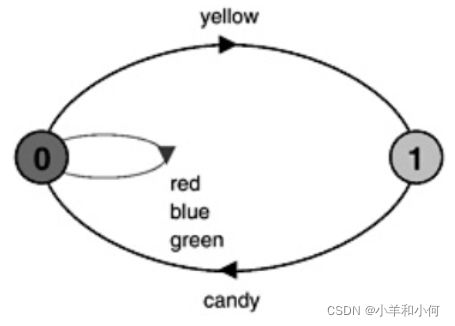
选择中元素的顺序没有任何意义。可以用一组动作标签来更简洁地表达FAULTY过程。该集合被解释为是对其成员之一的选择。

FAULTY = ({red,blue,green}-> FAULTY
         |yellow -> candy -> FAULTY
         ).

FAULTY的两个定义都产生完全相同的状态机图，如图下所示。请注意，红色、蓝色和绿色标注的是回到状态（0）的同一过渡。

再来看红绿灯的例子：

TRAFFIC_LIGHT = (button -> YELLOW | none -> GREEN),
GREEN = (green -> TRAFFIC_LIGHT),
YELLOW = (yellow -> RED),
RED = (red -> TRAFFIC_LIGHT).

如果按下行人按钮，交通灯就会变黄，然后变红，最后回到等待按钮被按下的状态。当按钮未按下时，该灯仍为绿色。

4. FSP—non-deterministic choice

(x -> P | x -> Q)

非确定性选择描述了一个Process，它最初参与到动作x，然后遵循流程P或Q。即P和Q的选择不受环境的控制。

下面是一个投掷硬币的模型，每一次投掷都有可能是头或者尾。

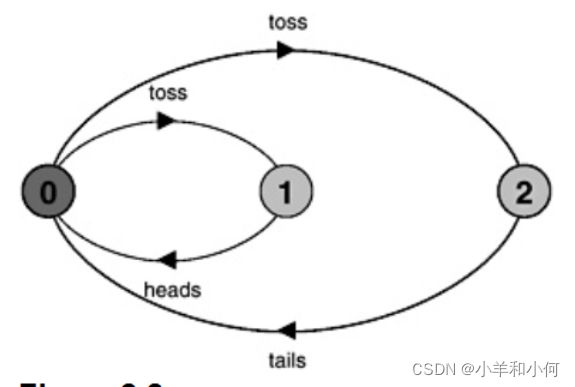
COIN = (toss -> heads -> COIN
       |toss -> tails -> COIN
       ).

 在一个抛掷动作之后，下一个动作可能是头或尾。下图给出了一个COIN过程的样本轨迹。

再来看我们的红绿灯模型。

TRAFFIC_LIGHT = ( button -> YELLOW
                | button -> green -> YELLOW
                | none -> GREEN 
                ),

GREEN = (green -> TRAFFIC_LIGHT),
YELLOW = (yellow -> RED),
RED = (red -> TRAFFIC_LIGHT).

如果按下行人按钮，交通灯可能立刻变黄，再变红；或者先变绿，随后变黄，再变红。

5. FSP—indexed processes

为了对可以取多个值的过程和动作进行建模，局部过程和动作标签都可以在FSP中被索引。这大大增加了符号的表达能力。索引总是有一个它们可以取的有限范围的值。这确保了我们在FSP中描述的模型是有限的，因此可能是可机械分析的。下面的过程是一个可以包含单个值的缓冲器——一个单槽缓冲器。它输入一个范围为0到3的值，然后输出这个值。

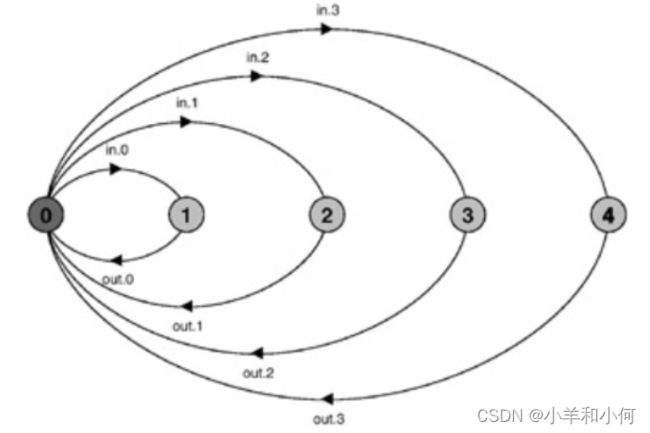
BUFF = (in[i:0..3] -> out[i] -> BUFF).

上面的表达式等同于

BUFF = ( in[0] -> out[0] -> BUFF
        | in[1] -> out[1] -> BUFF
        | in[2] -> out[2] -> BUFF
        | in[3] -> out[3] -> BUFF 
        ).

6. FSP—constants and ranges

为了提高可维护性并使模型通用化，常量可以被声明。常量可以只取整数值。此外，range，即整数的有限范围，可以被使用。

const N = 3
range T = 0..N

BUFF = (in[i:T] -> STORE[i]),
STORE[i:T] = (out[i] -> BUFF).

流程索引变量的范围是流程定义。动作标签索引的范围是它所出现的选择元素。因此，上面BUFF中索引变量的两个定义并不冲突。进程和动作标签都可以有一个以上的索引。下一个例子说明了这一点，一个进程输入两个值a和b，并输出它们的总和。请注意，索引变量上支持通常的算术运算。

const N = 1
range T = 0..N
range R = 0..2*N

SUM        = (in[a:T][b:T]->TOTAL[a+b]),
TOTAL[s:R] = (out[s]->SUM).

我们在SUM的定义中为常数N选择了一个较小的值，以确保下图的图形表示保持可读性。

7. FSP—Process Parameters

过程可以被参数化，以便可以用一般的形式描述它们，并针对特定的参数值进行建模。例如，在第5部分描述的单槽缓冲器可以被描述为一个参数化的过程，其值范围为0到N，如下所示。

BUFF = (in[i:0..3] -> out[i] -> BUFF).

变成

BUFF(N=3) = (in[i:0..N]->out[i]-> BUFF).

参数必须被赋予一个默认值，并且必须以大写字母开头。参数的范围是流程定义。另外，N可以被赋予一个固定的、恒定的值。如果N被用于一个以上的过程描述中，这可能更合适。

const N = 3
BUFF = (in[i:0..N]->out[i]-> BUFF).

8. FSP—guarded actions

根据机器的当前状态，将特定的行动定义为条件性的，往往是有用的。我们使用布尔守卫来表明，只有在满足其守卫的情况下，才能选择一个特定的动作。

被监视的行为，即

(when B x -> P | y -> Q)

当guard 条件B为真时，动作x和y都有资格被选择，否则，如果B为假，动作x不能被选择。注意前面是x和y，后面只限制了x的选择。

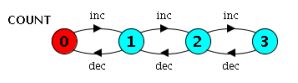
下面的例子（其状态机在下图中描述）是一个封装了一个计数变量的过程。计数可以通过inc操作增加，通过dec操作减少。计数不允许超过N或小于0。

COUNT (N=3) = COUNT[0],
COUNT[i:0..N] = (when(iCOUNT[i+1]
                |when(i>0) dec ->COUNT[i-1]
                ).

FSP只支持整数表达式；因此，零值用来表示假，任何非零值表示真。表达式的语法与C、C++和Java相同。

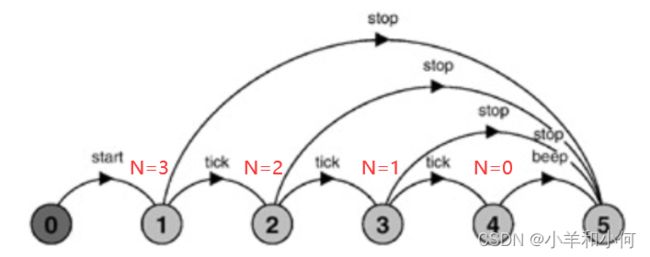
概述一个倒数计时器的实现：计时器一旦启动，每次递减计数时就会输出嘀嗒声，当它达到零时就会发出哔哔声。在任何时候，倒计时都可以通过一个停止动作来终止。倒计时器的模型描述如下；状态机在下图中。

COUNTDOWN (N=3)   = (start-> COUNTDOWN[N]),
COUNTDOWN[i:0..N] = (when(i>0) tick-> COUNTDOWN[i-1]
                    |when(i==0) beep-> STOP
                    |stop-> STOP
                    ).

 COUNTDOWN的可能轨迹集如下。

start → stop
start → tick → stop
start → tick → tick → stop
start → tick → tick → tick→stop
start → tick → tick → tick→beep

9. FSP—the STOP process

STOP流程是一个特殊的、预定义的流程，它不参与任何进一步的操作。它用于定义终止的进程。例如，考虑以下FSP模型，它执行了一个操作，然后终止：

ONESHOT = (once -> STOP).

 STOP process的定义：

const False = 0
P = (when (False) doanything -> P).

也就是说，当False为真时（永远不要）做任何动作（动作本身不重要），然后重复。

10. FSP—Process Alphabets

进程的字母表是它可以参与的行动的集合。

例如，8中的COUNTDOWN过程的字母表是{开始、停止、滴答、哔声}。一个流程只能参与其字母表中的动作；但是，它的字母表中可能有它从未参与的动作。例如，一个向存储位置写入的进程有可能向该位置写入任何32位的值；但是，它通常会写入一组更有限的值。在 FSP 中，进程的字母表是由它的定义中所引用的动作集隐含地决定的。

我们如何处理上述情况，即字母表中的动作集大于其定义中引用的动作集？答案是使用 FSP 提供的字母表扩展结构。下面定义的流程 WRITER 在其定义中使用了 write[1] 和 write[3] 的动作，但是定义了 write[0...3] 动作的字母表扩展 "+{...}"。一个进程的字母表是其隐含的字母表和任何指定的扩展的联合。因此，WRITER的字母表是write[0...3]。

WRITER = (write[1]->write[3]->WRITER)
         +{write[0..3]}.

应该注意的是，如果一个流程是用一个或多个本地流程定义的，每个本地流程的字母表与包围流程的字母表完全相同。包围进程的字母表只是所有本地定义中引用的动作集与任何明确指定的字母表扩展的结合。

以上就是使用FSP对单个过程建模的基础知识。