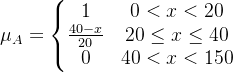模糊综合评价

引入

模糊性概念

对于某些量，比如身高体重，可以得到确切答案。而对于另外一些概念，比如美丑、高矮，就没有一个客观的界定，这些概念称为模糊性概念。

模糊是指客观事物差异的中间过渡中的“不分明性”。

实际上，我们处理现实的数学模型可以分为三大类：

• 确定型
• 随机型
• 模糊型

模糊集合和隶属函数

模糊集合：用来描述模糊性概念的集合

与经典集合相比，模糊集合承认“亦此亦彼”

数学上对模糊集合的刻画：

隶属函数 确定X上的一个模糊集合A，叫做A的隶属函数，叫做x对模糊集A的隶属度，记为,隶属度为0.5时最具模糊性。X中的元素越属于集合A，隶属度越接近于1

 比如说，我们要衡量“年轻”这个概念A="年轻"，X=(0, 150)表示年龄集合，我们可以给出一个隶属函数

实质上，隶属度，就是元素属于某个模糊集合的程度。

模糊集合的分类

• 偏小型：值越小，隶属度越大
• 中间型：值越中间，隶属度越大
• 偏大型 ：值越大，隶属度越大

隶属函数的确定方法

•         模糊统计法：找多个人对同一个模糊概念进行描述，比如问卷
•         借助已有的客观尺度：比如可以把“1-恩格尔系数”看作家庭相对于“小康家庭”的隶属度。
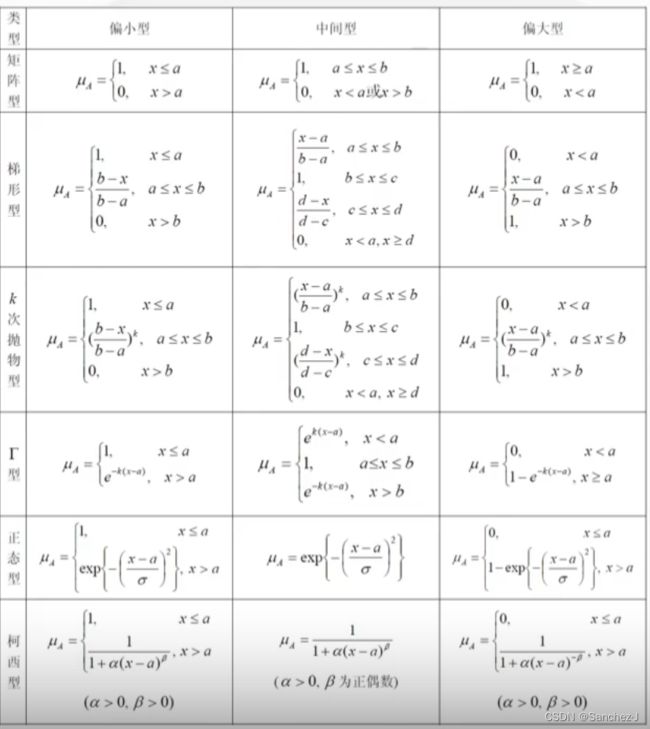
•         指派法：凭主观意愿，在确定模糊集合的所属分类后，给它指派一个隶属函数（可参考下表）。

评价问题概述 

        模糊评价问题是要把论域中的对象对应评语集中一个指定的评语或者将方案作为评语集并选择一个最优方案。 

        引入3个集合

•         因素集（评价指标集） U
•         评语集（评价的结果） V
•         权重集（指标的权重） A

        模糊综合评价模型就是给定对象，用因素集的指标进行评价，从评语集中找到一个最适合它的评语。 这里的“适合”用隶属度来衡量。

Python代码举例

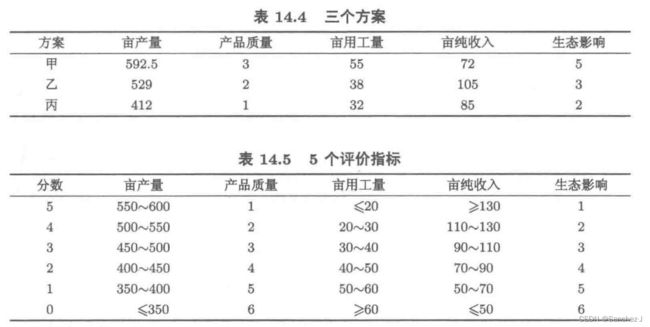
问题概要：

from numpy import array, piecewise, c_

data = array([[592.5, 3, 55, 72, 5], [529, 2, 38, 105, 3], [412, 1, 32, 85, 2]])
data_transposed = data.T
# 对数组data进行转置。现在它有五行三列。
membership_function1 = lambda x: piecewise(x, [(350 < x) & (x < 600), x >= 600], [lambda x: (x - 350) / 250., 1])
membership_function2 = lambda x: piecewise(x, [(1.0 < x) & (x < 6.0), (x <= 1.0)], [lambda x: 1 - (x - 1) / 5.0, 1])
membership_function3 = lambda x: piecewise(x, [(20 < x) & (x < 60), x <= 20], [lambda x: 1 - (x - 20) / 40., 1])
membership_function4 = lambda x: piecewise(x, [(50 < x) & (x < 130), x >= 130], [lambda x: (x - 50) / 80., 1])
membership_function5 = lambda x: piecewise(x, [(1 < x) & (x < 6), x <= 1], [lambda x: 1 - (x - 1) / 5., 1])
# 建立的隶属函数
membership_matrix = c_[membership_function1(data_transposed[0]),
membership_function2(data_transposed[1]),
membership_function3(data_transposed[2]),
membership_function4(data_transposed[3]),
membership_function5(data_transposed[4])].T
# 将 lambda 函数应用于转置后的数组 data 的每一列，并使用 c_ 沿着第二轴连接结果。
# 最终的结果然后再次进行转置。
weights = array([0.2, 0.1, 0.15, 0.3, 0.25])
# 创建权重数组 weights。
aggregated_result = weights.dot(membership_matrix)
# 计算权重数组 weights 和转置数组 membership_matrix 的点积。
print('Membership Matrix=', membership_matrix, '\n---------------------------\n', 'Aggregated Result=',
      aggregated_result)
# 输出综合评价矩阵和隶属度矩阵
# 根据隶属度原则，乙方案的隶属度最大，选乙。

 结果：

Membership Matrix= [

[0.97   0.716  0.248 ]
[0.6    0.8    1.    ]
[0.125  0.55   0.7   ]
[0.275  0.6875 0.4375]
[0.2    0.6    0.8   ]

] 
---------------------------
 Aggregated Result= [0.40525 0.66195 0.58585]