二叉树-堆实现
目录
Test.c测试代码
test1
test2
test3
Test.c总代码
Heap.h头文件&函数声明
头文件
函数声明
Heap.h总代码
Heap.c函数实现
☁HeapInit初始化
☁HeapDestroy销毁
☁HeapPush插入数据
【1】插入数据
【2】向上调整Adjustup❗
数据交换Swap
☁HeapPop删除数据
【1】交换数据
【2】删除数据
【3】向下调整Adjustdown❗
假设法找Child
数据交换Swap
☁HeapTop堆顶元素
☁HeapSize堆元素个数
☁HeapEmpty判断为空否
Heap.c总代码
拖了很久的【堆】,本周主要学习就是【数据结构】。本章【堆】是以【小堆】为例子。
- 堆表面是数组,内核是完全二叉树/满二叉树
- ❗HeapPush
- ❗HeapPop
- 函数如果需要多次复用才会提取出来
- free会对NULL进行检查
- 用循环写起来很方便的代码就不要使用递归
- do while循环用于无论循环条件如何,循环都会执行一次
- 步骤--注意事项--循环结束条件--时间复杂度(下篇重点讲)
Test.c测试代码
#include"Heap.h"
int main()
{
HP php;
//HP*ph=&php
//test1(&php);
test2(&php);
test3(&php);
return 0;
}
test1
//建堆
void test1(HP* ph)
{
int a[] = { 4,5,3,7,8,2,1,9,10 };
HeapInit(ph);
int i = 0;
for (i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
HeapPush(ph, a[i]);
}
}test2
//找出堆的前K个数字
void test2(HP* ph)
{
int a[] = { 4,5,3,7,8,2,1,9,10 };
HeapInit(ph);
int i = 0;
int k = 5;
for (i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
HeapPush(ph, a[i]);
}
while (k--)
{
printf("%d ", HeapTop(ph));
HeapPop(ph);
}
printf("\n");
}test3
//排序--升序
void test3(HP* ph)
{
int a[] = { 4,5,3,7,8,2,1,9,10 };
HeapInit(ph);
int i = 0;
for (i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
HeapPush(ph, a[i]);
}
while (HeapEmpty(ph))//为NULLflase
{
printf("%d ", HeapTop(ph));
HeapPop(ph);
}
}Test.c总代码
#include"Heap.h"
//建堆
void test1(HP* ph)
{
int a[] = { 4,5,3,7,8,2,1,9,10 };
HeapInit(ph);
int i = 0;
for (i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
HeapPush(ph, a[i]);
}
}
//找出堆的前K个数字
void test2(HP* ph)
{
int a[] = { 4,5,3,7,8,2,1,9,10 };
HeapInit(ph);
int i = 0;
int k = 5;
for (i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
HeapPush(ph, a[i]);
}
while (k--)
{
printf("%d ", HeapTop(ph));
HeapPop(ph);
}
printf("\n");
}
void test3(HP* ph)
{
int a[] = { 4,5,3,7,8,2,1,9,10 };
HeapInit(ph);
int i = 0;
for (i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
HeapPush(ph, a[i]);
}
while (HeapEmpty(ph))//为NULLflase
{
printf("%d ", HeapTop(ph));
HeapPop(ph);
}
}
int main()
{
HP php;
//HP*ph=&php
//test1(&php);
test2(&php);
test3(&php);
return 0;
}Heap.h头文件&函数声明
头文件
#pragma once
#include
#include
#include
#include
#include typedef int HpDataType;
//定义堆结构体
typedef struct Heap
{
HpDataType* a;
int size;
int capacity;
}HP;
函数声明
//常用接口
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php,HpDataType x);
void HeapPop(HP* php);
HpDataType HeapTop(HP* php);
int HeapSize(HP* php);
bool HeapEmpty(HP* php);
Heap.h总代码
#pragma once
#include
#include
#include
#include
#include
typedef int HpDataType;
//定义堆结构体
typedef struct Heap
{
HpDataType* a;
int size;
int capacity;
}HP;
//常用接口
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php,HpDataType x);
void HeapPop(HP* php);
HpDataType HeapTop(HP* php);
int HeapSize(HP* php);
bool HeapEmpty(HP* php); Heap.c函数实现
☁HeapInit初始化
#include"Heap.h"
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}☁HeapDestroy销毁
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);//不用担心为NULL,free会对NULL做检查
php->size = php->capacity = 0;
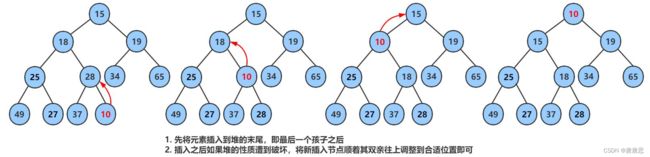
}☁HeapPush插入数据
先插入一个10到数组的尾上,再进行向上调整算法,直到满足堆。
【1】插入数据
void HeapPush(HP* php, HpDataType x)
{
assert(php);
//扩容
if (php->size == php->capacity)
{
int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;
HpDataType* tmp = (HpDataType*)realloc(php->a, newcapacity * sizeof(HpDataType));
if (tmp == NULL)
{
printf("fail realloc");
return;
}
php->capacity = newcapacity;
php->a = tmp;
}
//插入数据
php->a[php->size] = x;
php->size++;
//向上调整//数组,调整元素下标
AdjustUp(php->a, php->size - 1);
}【2】向上调整Adjustup❗
//向上调整算法
void AdjustUp(HpDataType* a, int child)
{
int parent = (child - 1) / 2;
while ( child > 0 )//此刻parent已经数组越界
{
if (a[child] < a[parent])
{
//交换
Swap(&a[child], &a[parent]);
child = parent;
parent = (parent - 1) / 2;
}
else//child>=parent
{
break;
}
}
}数据交换Swap
//交换
void Swap(HpDataType* H1, HpDataType* H2)
{
HpDataType tmp = *H1;
*H1 = *H2;
*H2 = tmp;
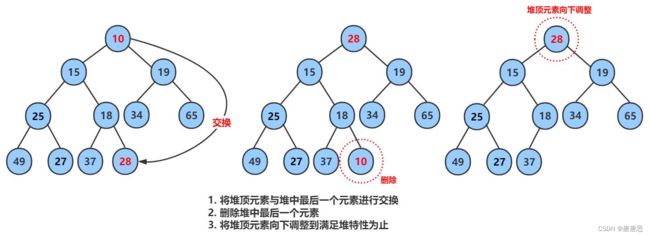
}☁HeapPop删除数据
删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。
//删除
void HeapPop(HP* php)
{
assert(php);
assert(php->size);
//1.交换
Swap(&php->a[0], &php->a[php->size - 1]);
//2.删除
php->size--;
//3.向下调整--数组,结束条件size有关,调整的位置parent
Adjustdown(php->a, php->size, 0);
}【1】交换数据
//1.交换
Swap(&php->a[0], &php->a[php->size - 1]);【2】删除数据
//2.删除
php->size--;【3】向下调整Adjustdown❗
//3.向下调整--数组,结束条件size有关,调整的位置parent
Adjustdown(php->a, php->size, 0);
//向下调整
void Adjustdown(HpDataType* a, int size, int parent)
{
//假设法
int child = parent * 2 + 1;
while (child < size )//why child < size && child+1假设法找Child
int child = parent * 2 + 1;
if (a[child + 1] < a[child])
{
child++;
}数据交换Swap
//交换
void Swap(HpDataType* H1, HpDataType* H2)
{
HpDataType tmp = *H1;
*H1 = *H2;
*H2 = tmp;
}☁HeapTop堆顶元素
HpDataType HeapTop(HP* php)
{
assert(php);
assert(php->size);
return php->a[0];
}☁HeapSize堆元素个数
int HeapSize(HP* php)
{
assert(php);
return php->size;
}☁HeapEmpty判断为空否
bool HeapEmpty(HP* php)
{
assert(php);
return php->size != 0;//!=0是true不为NULL执行 ==0 flase 不执行
}Heap.c总代码
#include"Heap.h"
void HeapInit(HP* php)
{
assert(php);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);//不用担心为NULL,free会对NULL做检查
php->size = php->capacity = 0;
}
//交换
void Swap(HpDataType* H1, HpDataType* H2)
{
HpDataType tmp = *H1;
*H1 = *H2;
*H2 = tmp;
}
//向上调整算法
void AdjustUp(HpDataType* a, int child)
{
int parent = (child - 1) / 2;
while ( child > 0 )//此刻parent已经数组越界
{
if (a[child] < a[parent])
{
//交换
Swap(&a[child], &a[parent]);
child = parent;
parent = (parent - 1) / 2;
}
else//child>=parent
{
break;
}
}
}
void HeapPush(HP* php, HpDataType x)
{
assert(php);
//扩容
if (php->size == php->capacity)
{
int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;
HpDataType* tmp = (HpDataType*)realloc(php->a, newcapacity * sizeof(HpDataType));
if (tmp == NULL)
{
printf("fail realloc");
return;
}
php->capacity = newcapacity;
php->a = tmp;
}
//插入数据
php->a[php->size] = x;
php->size++;
//向上调整//数组,调整元素下标
AdjustUp(php->a, php->size - 1);
}
//向下调整
void Adjustdown(HpDataType* a, int size, int parent)
{
//假设法
int child = parent * 2 + 1;
while (child < size )//why child < size && child+1当然,【大堆】只要改变大小符号即可,如果你不想要改变,可以使用【回调函数】!!
感谢大家的阅读,若有错误和不足,欢迎指正!希望本周可以结束【初阶数据结构】