堆(Heap)数据结构

在阅读本文前，需要明确的是，这里的“堆”是一种数据结构，而不是JVM里的垃圾回收里的堆存储结构。堆可看成一种特殊的树，这里以二叉堆为例介绍堆。

堆的性质

二叉堆可以分为两种形式：最大堆和最小堆。在最大堆中，除了根结点以外的节点的值至多与其父节点一样大。也就是说，最大堆中的最大元素存放在根节点中，并且在任一子树中，该子树所包含的所有节点的值都不大于该子树根节点的值。同理，最小堆中的最小元素存放在根节点中，并且在任一子树中，该子树所包含的所有节点的值都不小于该子树根节点的值。
此外，二叉堆是紧凑的，是一棵完全二叉树或者近似完全二叉树。

堆的存储结构

与二叉树一样，堆的常见存储结构也有两种：顺序存储结构、链式存储结构。这里仅介绍顺序存储结构，链式存储结构请自行学习。
表示堆的数组A包括两个属性：A.length记录数组元素的个数，A.heap-size表示该数组中堆元素个数。也就是说，虽然A[1…A.length]可能存有数据，但只有A[1…A.heap-size]存放的是堆的有效元素。堆的根节点是A[1]。这样给定一个节点的下标$i$，则可以很容易计算其父结点、左孩子、右孩子：

$$PARENT(i)$$
$$return\lfloor i/2\rfloor$$

$$LEFT(i)$$
$$return(2i)$$

$$RIGHT(i)$$
$$return(2i+1)$$

这里给出堆的链式存储和顺序存储示例：

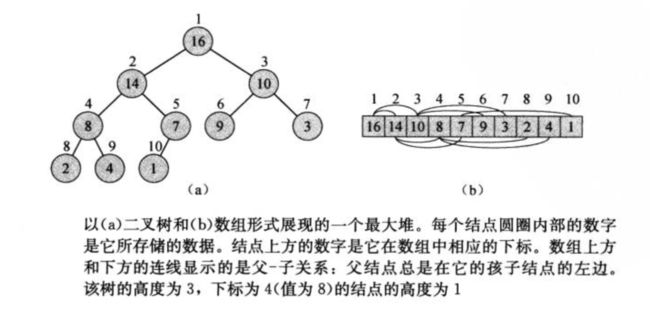
此外，对于最大堆来说：
(1) 最大堆上任一子树，该子树所包含的最大元素都在该子树的根结点上。
(2) 当用数组表示存储n个元素的堆时，叶结点洗标分别是$\lfloor n/2\rfloor +1$,$\lfloor n/2\rfloor +2$,…,$\lfloor n/2\rfloor +n$。

堆的操作

堆上支持的操作有很多，这里将基于最大堆解释一些基本操作，最小堆同理。
(1) maxHeapify: 其时间复杂度为$O(logn)$，用于维护最大堆的性质。
(2) buildMaxHeap: 其时间复杂度为$O(h)$，其中$h$表示树的高度，用于构造最大堆。
(3) sortHeap: 其时间复杂度为$O(nlogn)$，用于对一个数组进行排序。
(4) 优先队列：基于堆原理，可以优先队列。

维护堆的性质

假定数组A后i-1个元素已经构成一个最大堆且第i-1个元素为根结点，现在向这个数组增加第i个元素，使用maxHeapify维护最大堆。该算法的核心思想是通过让A[i]在最大堆中“逐级下降”，从而使得以下标i为根结点的子树重新遵循最大堆的性质。其伪代码实现如下：

maxHeapify(A, i)
// 左子树最大堆的根结点
l = LEFT(i)
// 右子树最大堆的根结点
r = RIGHT(i)
if(l <= A.heap.size && A[l] > A[i])
    largest = l
else
    largest = i
if(r <= A.heap.size && A[r] > A[largest])
    largest = r
// 逐级下降
if(larget != i)
    exchange(A[i], A[largest])
    maxHeapify(A, largest)

维护堆的性质是最大堆的基本操作，后面的构建最大堆、堆排序等实现都是基于该操作实现。更多示例说明可以参考算法导论一书。

构建最大堆

维护最大堆性质时，我们要求堆中的元素从后向前保持最大堆性质。所以，在构建最大堆时，我们用自底向上的方式将A[n]的数组转换成最大堆。另外，由于子数组$\lfloor n/2\rfloor +1$,$\lfloor n/2\rfloor +2$,…,$\lfloor n/2\rfloor +n$都是树的叶结点，而每个叶结点都可看成只包含一个元素的堆，所以仅需对其他节点调用maxHeapify即可完成最大堆的构建。伪代码如下：

buildMaxHeap(A)
A.heap.size = A.length
for(i=A.length/2 downto 1)
    maxHeapify(A, i)

该算法的正确性证明可参考算法导论一书。

堆排序

最大堆可以保证根结点值最大，我们可以利用这一性质实现堆排序。初始时，先利用buildMaxHeap(A)将数组A构建成最大堆，这样A[1]就是数组中的最大元素。然后，让数组中第i个元素与A[1]互换，然后对前i-1个元素进行堆排序，这样A[1]可以第n-i大元素。其伪代码实现如下：

sort(A)
// 先构建最大堆
buildMaxHeap(A)
// 再找出最大元素之外的其他元素
for(i = A.length downto 2)
    exchange(A[i], A[1])
    A.heap.size = A.heap.size - 1
    maxHeapify(A, i)

这样，基于最大堆就可实现一个升序的排序数组。如果期望实现一个降序的数组，则可类比使用最小堆实现。

优先队列(Priority Queue)

堆数据结构的应用有很多，其中比较常见的应用就是优先队列。与堆一样，优先队列也有最大优先队列和最小优先队列。这里仅介绍最大优先队列。优先队列是一种用来维护由一组元素构成的集合S的数据结构，其中每个元素都有一个相关的值，称为关键字(key)。一个最大优先队列支持以下操作：
(1) insert(S, x)，将元素x插入到集合S中。
(2) max(S)，返回S中关键字最大的元素。
(3) extractMax(S)，移除并返回S中关键字最大的元素。
(4) increaseKey(S, x, k)，将元素x的关键字的值增加到k，注意，这里要求k大于元素x原来的值
注意，JDK提供PriorityQueue可以让开发者方便的使用队列（也可以将优先队列作为堆使用）

max(A)

对于基于堆构建的优先队列来说，第一个元素就是最大值。其伪代码如下：

max(A)
return A[i]

extractMax(A)

移除优先队列中关键字最大的元素，这里以第一次移除为例，只需先取出A[1]，然后对2…n元素维护堆的性质。伪代码如下：

extractMax(A)
max = A[1]
A[1] = A[A.heap.size]
A.heap.size = A.heap.size - 1
maxHeapify(A, i)
return max

increaseKey(A, i, keyNewValue)

在优先队列中，期望增加元素的关键字，对于使用堆实现的优先队列来说，这可能会破坏最大堆的性质。因此，新增元素的关键字总是伴随着数据交换。伪代码如下：

increaseKey(A, i, keyNewValue)
A[i] = keyNewValue
while(i > 1 && A[PARENT(i)] < A[i])
    exchange(A[PARENT(i)], A[i])
    i = PARENT(i)

insert(A, key)

将关键字key插入到数组A中。首先，需要新增一个叶结点来扩展最大堆。然后调用increaseKey为新结点设置对应的值，并使其保持最大堆性质。伪代码如下：

insert(A, key)
A.heap.size = A.heap.size + 1
A[A.heap.size] = MIN_VALUE
increaseKey(A, A.heap.size, key)

参考

https://leetcode-cn.com/tag/heap-priority-queue/problemset/ 堆（优先队列）
《算法导论》 第六章 堆排序 第三版 Tomas H. Cormen etc. 殷建平 等译
https://zhuanlan.zhihu.com/p/124885051 排序算法之堆排序