LeetCode | 84. 柱状图中最大的矩形
LeetCode | 84. 柱状图中最大的矩形
- 一、题目描述
- 二、思路及题解
-
- 2.1、方法一:暴力解法
- 2.2、方法二:栈
一、题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例:

示例说明:
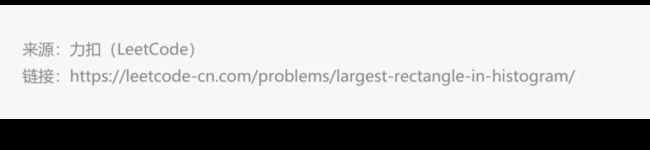
如下是示例输入的柱状图,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]
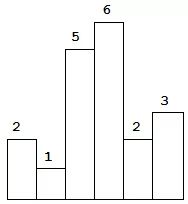
根据题目要求可得到,图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。如下图:
二、思路及题解
首先,拿到这道题,想必很多人和我一样,想到的就是暴力解法,毕竟所有解法都是在优化暴力解法嘛~ 。那我们一起来看看我们熟悉的暴力解法?
2.1、方法一:暴力解法
暴力无外乎于求解所有的可能,找出其中满足要求的解!那么我们可以这样来操作:依次遍历柱形的高度数组,对于每一个矩形分别向它的两边扩散,求出以当前高度构成的矩形的最大面积,也就最大宽度。
为此,我们需要进行如下操作:
-
向前看:从当前矩形往前找,找到小于当前矩形高度的矩形或者到第一个矩形就停止,获取其下标;
-
向后看:从当前矩形往后找,找到小于当前矩形高度的矩阵或者到最后一个矩形就停止,获取其下标;
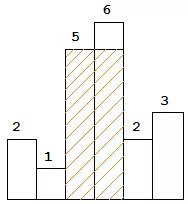
例如 [2,1,5,6,2,3] 的求解过程:如下图:

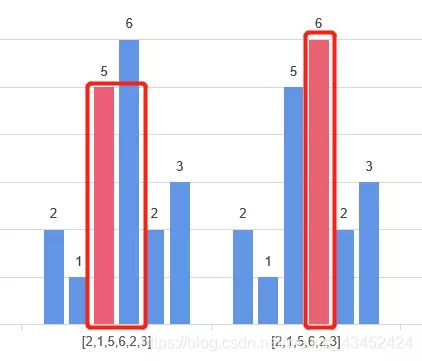

计算结果如下:

示例代码(Java):

复杂度分析:
- 时间复杂度O(N^2):N输入高度数组长度。
- 空间复杂度O(1).
2.2、方法二:栈
分析暴力算法的复杂度,我们可以知道,暴力算法的时间复杂度为O(N^2),而空间复杂度为O(1 ) 。同时暴力算法中,在计算矩形宽度时,我们不断的重复去计算向前和向后满足要求的长度,所以造成一些重复的计算。因此,我们可以将这些计算结果记录下来,从而降低时间复杂度。
利用空间换时间的思路,用到的数据结构是栈~~,至于为什么?请保持疑问,继续往下看。
由于需要获知矩形的面积,我们需要记录矩形的面积,但是题目已经给出了矩形的高度,那么我们只需去获知矩形的宽度,记录矩形宽度即可。对于矩形宽度很容易根据数组的下标计算。因此,我们只需根据矩形的下标计算出矩形的宽,再记录它即可。
可能这样说比较晦涩,咱们直接借用例子说明,如下:
- 首先,遍历到高度为2的矩形,下一个矩形还未知,所以目前还无法获知该矩形高度对应的矩形宽度。那就继续遍历~
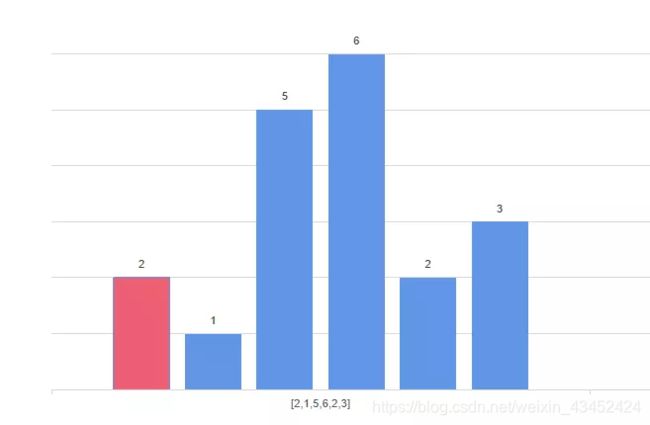
- 这时遍历到高度为1的矩形,还是不知该矩形右边的矩形,因此无法计算出以该矩形高度构成的最大矩形面积。可是,它的前一个高度为2的矩形,高度比当前矩形的高度(1)高,无法继续扩展矩形宽度了,因此可以知道这个高度为2的矩形宽度为1,面积为2。记录完后,便可将其“去除掉”。
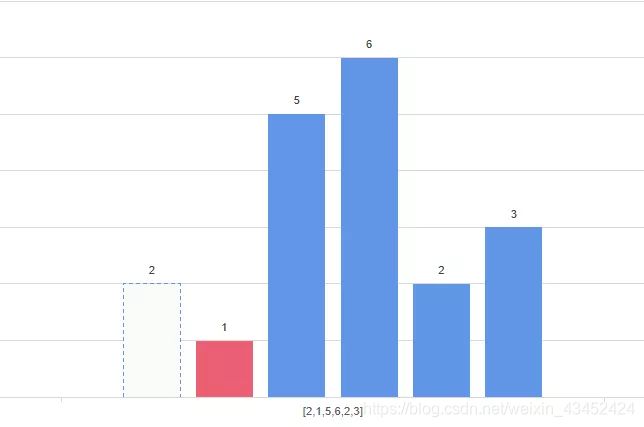
- 遍历到高度为5的矩形,同样的以当前看到柱形为高度的矩形的最大面积也是不知道的,因为我们还要继续看右边高度的情况。那么它的左右有没有可以确定的柱形呢?没有,这是因为 5 > 1 ,我们看后面马上就出现了 6,不管是 1 这个柱形还是 5 这个柱形,都还可以向右边扩展;
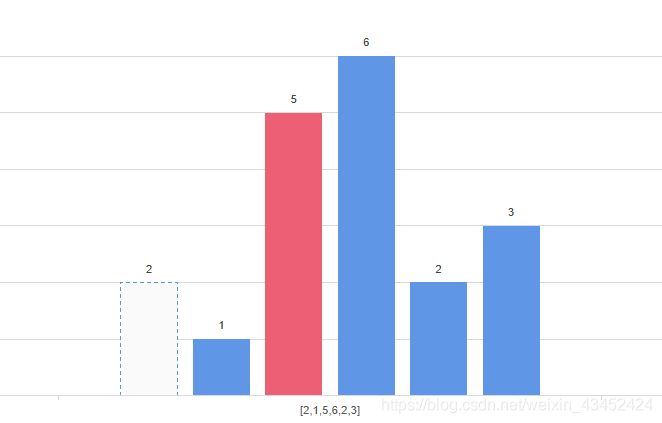
- 遍历到6,如3所述,以1、5、6为高度的矩形最大面积还无法确定。

- 之后便是高度为2 的矩形元素,此时2<6,因此可以确定高度为6的矩形面积,换句话说就是矩形的宽度。width = 1,面积为6;
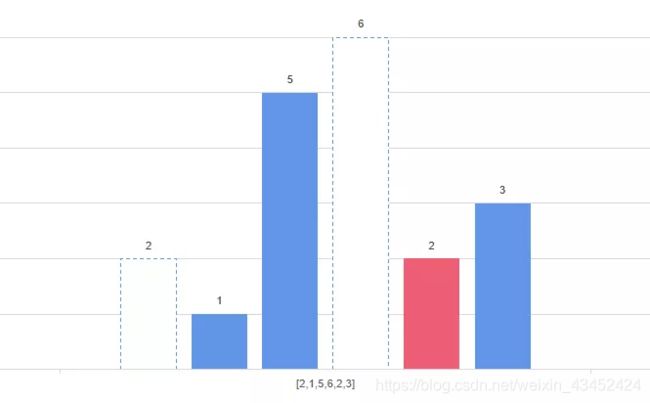
- 此时5>2,依然可以计算出以该矩形高度为高的矩形最大面积为5*2=10。
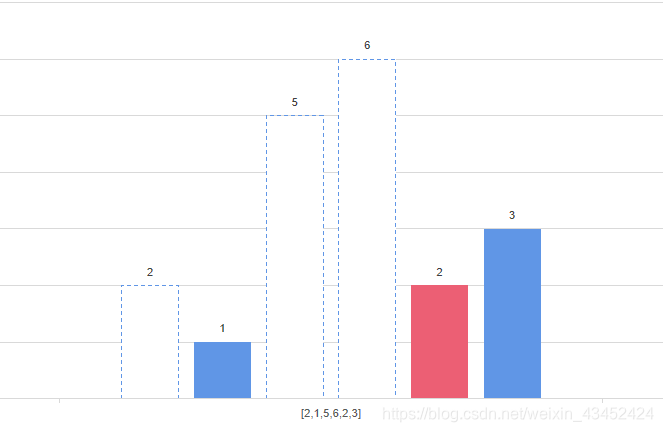
此时,观察计算下标为0、2、3对应元素为高的矩形面积时,我们可以发现该矩形的宽就是该矩形左右两边的矩形下标之差-1.如高度为6的矩形:width = indexOf2 - indexOf5 => width = 4-2-1=1。同时我们发现矩形面积的计算遵循着先遍历后计算的特点,比较符合数据结构中栈的特点,因此,我们就需要使用栈来记录对应高度的矩形的宽度。
可是有人会问了,那么第一个元素和最后一个元素的宽度如何计算呢?它们没有左边或者右边元素啊?无法获取其长度啊?所以我们这里提出了数据结构中快速排序的“哨兵思想”,在数组的开始和最后各加一个元素(0或者符合要求的),不并入计算面积,但是用于计算数组中矩形的宽度。
例如,计算第一个矩形2的宽度,width = index1 - index0.5 = 2 - 0 - 1= 1,如下图:
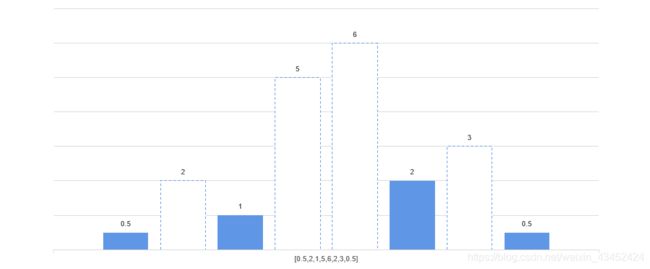
- 由于2>1,因此继续遍历到高度为3的矩形。此时,已经遍历完数组了,所以3对应矩形的宽度为:width = index0.5-index1-1=7-2-1=4,因此该高度对应矩形的宽度为4,面积为8 。
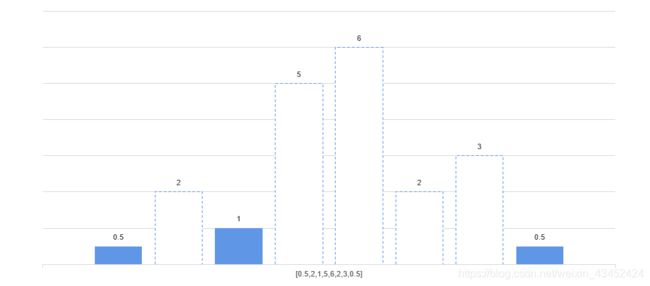
- 因此,高度为1的矩形对应的宽度为with=7-0-1=6;

总结来说,就是使用栈来记录对应高所构成的矩形宽度,从而使用栈的特点来计算每个高对应的最大宽度的矩形面积。
-
width = nextIndex - preIndex - 1。
-
使用栈来存储矩形对应的宽。
-
当当前元素严格小于前一个元素(栈顶元素对应的数组下标的元素)时候,便可确定前一个元素对应矩形的最大面积。
-
在数组开头和最后添加“哨兵”,因此解决计算第一个元素和最后一个元素对应矩形的宽。
示例代码(Java):
class Solution {
public int largestRectangleArea(int[] heights) {
int len = heights.length ;
if(len == 0){
return 0;
}
if(len == 1){
return heights[0];
}
int res = 0;
//创建新的数组,存储加入的哨兵
int[] newHeights = new int[len+2];
newHeights[0] = 0;
System.arraycopy(heights,0,newHeights,1,len);
newHeights[len+1]=0;
len+=2;
heights = newHeights;
Deque<Integer> stack = new ArrayDeque<>(len);
//放入哨兵后,在循环中就不用栈非空判断
stack.addLast(0);
for(int i=1;i<len;i++){
while(heights[i]<heights[stack.peekLast()]){
int curHeight = heights[stack.pollLast()];
int curWidth = i -stack.peekLast()-1;
res = Math.max(res,curHeight*curWidth);
}
stack.addLast(i);
}
return res;
}
}
复杂度分析:
-
时间复杂度O(N)。
-
空间复杂度O(N)。