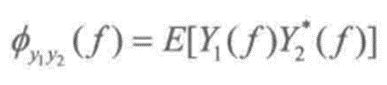雷达DoA估计的跨行业应用--麦克风阵列声源定位（Matlab仿真）

一、概述

       麦克风阵列： 麦克风阵列是由一定数目的声学传感器（麦克风）按照一定规则排列的多麦克风系统，而基于麦克风阵列的声源定位是指用麦克风拾取声音信号，通过对麦克风阵列的各路输出信号进行分析和处理，得到一个或者多个声源的位置信息。

        麦克风阵列系统的声源定位技术研究意义在于： 输入的信息只有两个方向难以确定声源的位置，人类的听觉系统主要取决于头和外耳气压差声波实现声源定位。假使没有这个压力差，只能定位在平面上声源的位置，但就无法知道声音是从前面，或从后面传来的。因此，由人的听觉系统，科技研发人员得到了灵感，使用多个麦克风系统可以实现在三维空间中的声源位置的定位，麦克风的数量越多，所接收到的信息量也越多。声源的声源定位和声源增强是实现智能处理的两个关键问题，而声源定位是实现语音增强的前提和基础。一个麦克风的信息量较少，使得声源定位所需的信息缺乏，而麦克风阵列克服了上述缺点，充分利用每个麦克风信号之间的数据相关性，并加以融合，可以实现声源定位。

        麦克风阵列声源定位技术的应用： 广泛应用于国防、智能机器人、视频会议及语音增强等众多领域,尤其在当下以智能办公和智能家居为主要室内场景的远场语音交互系统中。

二、声源定位模型

        声源定位可以分为近场模型和远场模型，顾名思义，离麦克风近则符合近场模型，离得远则符合远场模型 。

        假设L为阵列间距，λ为声波波长，M为声源与麦克风的距离，定义为远近场临界值。

        当 M<时，符合近场模型，此时声源到达麦克风阵列的波形视为球面波。

        当M>时，符合远场模型，此时声源到达麦克风阵列的波形视为平面波。

        可听声的机械波频带为20Hz ~20000Hz，机械波波长大约在1.7cm ~ 17m（声速取340m/s）。然而在现实生活中，过高频率或过低频率的声波都是非常少量的，以人的声音为例，人语音频带的范围大概为300Hz至3400Hz，波长范围为0.1m~ 1.12m，当阵列间隔取4cm时，远近场临界值范围为 0m~3.2m。若取中间值，则可以认为1.6m内符合近场模型，1.6m外符合远场模型。

1 近场模型

        当 M<时，符合近场模型，此时声源到达麦克风阵列的波形视为球面波。

        近场模型至少需要3个麦克风，以最简单的3麦克风模型为例（如图：y1、y2、y3）。假设τ12、τ13分别表示第一个麦克分与第二和第三个麦克风之间的时延，那么有：

      

        

       其中，c为声速。标准大气压、15°条件下，声速为340m/s。

       根据麦克风阵列的的几何关系，由余弦定理，可以得到：

      

      

       其中，τ12、τ13可以通过互相关GCC求得，且c、d 为已知。结合上述公式即可求出未知量 r_1、r_2、r_3、θ，结合坐标系可以求出s(k)的坐标。

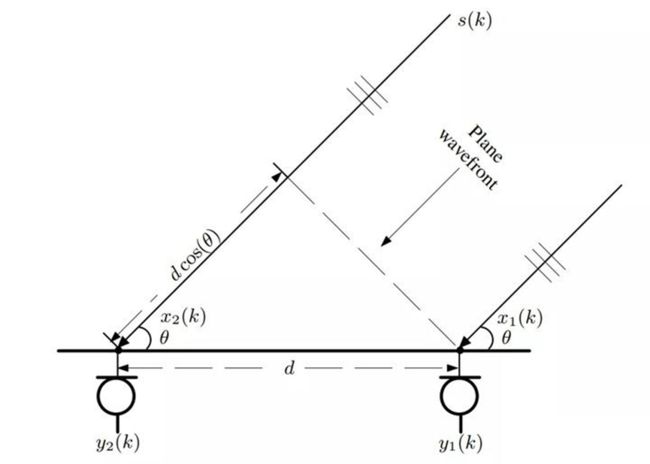
2 远场模型

       当M<时，符合远场模型，此时声源到达麦克风阵列的波形视为平面波。

        对于两个麦克风的情况，只能计算出方位角，无法计算出方位距离。假设 τ 为声波到达两个麦克风之间的时延，则有

      

        

三、声源定位算法原理和仿真

        目前基于麦克风阵列的声源定位方法主要有三种：基于最大输出功率的可控波束成形的定位方法、基于高分辨谱估计的定位方法、基于到达时延差估计的定位方法(Time Difference of Arrival，TDOA)。

1 基于最大输出功率的可控波束成形定位法

        波束形成法的原理是将麦克风接收到的信号进行滤波加权求和来形成波束，按照一定的规律对声源位置进行搜索，当麦克风达到最大输出功率时，为时搜索到的声源位置即为真实的声源方位。

        DBF是Digital Beam Forming的缩写，译为数字波束形成或数字波束合成。数字波束形成技术是天线波束形成原理与数字信号处理技术相结合的产物，其广泛应用于阵列信号处理领域。

        DBF体现的是声源信号的空域选择性，许多传统波束形成方法具有线性处理结构；波束形成需要考虑三个方面：

        1)麦克风阵列个数；

        2)性能；

        3)鲁棒性。

        在麦克风较少时，波束形成的空域选择性差，当麦克风数量较多时，其波束3dB带宽较为窄，如果估计的目标声源方向有稍有偏差，带来的影响也更大，鲁棒性不好。通常鲁棒性和性能是对矛盾体，需要均衡来看。

        以均匀线阵波束形成模型为例：

        按窄带模型分析：

        ​​​​​​​

        可以写成矩阵形式：

        ​​​​​​​

       其中a(θ)为方向矢量或导向矢量（Steering Vector），波束形成主要是针对各个接收信号X进行权重相加，峰值位置对应的角度即是声源方向角。

        Matlab仿真代码及结果如下。

% DBF均匀阵列的dbf测角
clear all; clc; close all;

%构造阵列和信号
array_uni = 0:1:13;                 % 同样孔径下的均匀阵列
theta = -15;                        % 目标角度
dd     = 0.5;                       % 均匀间隔
snr    = 20; 
A_uni = exp(-1i*2*pi*dd*sind(theta).*array_uni.');  
x_uni = awgn(A_uni,snr);            % 添加噪声

%使用dbf测角
thetascan = linspace(-90,90,1024);
a_uni  = exp(1i*2*pi*dd*sind(thetascan).'*array_uni);
p_uni = x_uni.'*a_uni.';  p_uni = 10*log10(abs(p_uni)./max(abs(p_uni)));

[max_value,index] = max(p_uni);
theta_est = thetascan(index);
est_error = abs(theta_est - theta);

figure(1)
plot(thetascan,p_uni);hold on;
plot([theta,theta],ylim,'m-.');
xlabel('xita/°');ylabel('amplitude/dB');title(['DBF测角结果 SNR = ' num2str(snr)]);

2 基于高分辨谱估计的定位法

        基于高分辨率谱估计的定位方法通过分解协方差矩阵估计声源方位。适合多个声源的情况，且声源的分辨率与阵列尺寸无关，突破了物理限制。该方法的优点是不受采样频率限制，且在一定程度下可以实现任意程度的定位，但是该方法计算复杂度较高，抗噪和抗混响性能较差，因此该方法适合在一些特定的环境下使用。这类方法可以拓展到宽带处理，但是对误差十分敏感（如麦克风单体误差，通道误差），适合远场模型，且矩阵运算量巨大。

        MUSIC（Multiple Signal Classification）算法是一种典型的谱估计算法，该算法建立在一下假设基础上：

        ①、噪声为高斯分布，每个麦克风之间的噪声分布为随机过程，之间相互独立，空间平稳，即每个麦克风噪声方差相等。

        ②、要求空间信号为高斯平稳随机过程，且与单元麦噪声互不相干，相互独立。

        ③、目标声源数目小于阵列元数目。

        ④、阵元间隔不大于来波信号中频率最高波长的1/2。

        MUSIC算法是空间谱估计技术的代表之一，它利用特征结构分析。其基本原理是将协方差矩阵进行特征值分解。它通常把空间信号分为两种，一种是信号特征向量对应的信号空间，另一种是噪声向量对应的噪声空间，利用噪声空间和信号空间的正交性原理，构造空间谱函数进行搜索，从而预估出DOA信息。

        阵列数据的协方差矩阵为：

        

        其中，RS和RN分别为信源的协方差矩阵和噪源的协方差矩阵。

        通过对阵列协方差矩阵进行特征值分解，将特征值进行升序排列，其中有D个较大的特征值，对应于声源信号，而有M-D个较小的特征值，对应于噪声信号。

        设λi为第i个特征值，vi为其对应的特征向量，则：

        

        设λi = σ2是R的最小特征值，则：

        

        将R = ARS AH + σ2I代入上式得：

        

        化简可得：

        

        由于AHA是满秩矩阵，(AHA)−1存在，而RS−1也存在，则上式同乘以RS−1(AHA)−1AH后变成：

        

        于是有AHvi = 0 , i = D + 1 , D + 2 , . . . , M，故可以用噪声向量来求信号源的角度。先构造噪声矩阵En

        

        最后定义空间谱P ( θ )

        

        其中a为上一节中的方向导向向量，通过遍历θ，即可得到一个空间的功率谱，寻找其最值即可寻得DOA方向角。二维的估计也相同，增加一个遍历的维度即可。

        Matlab仿真代码及结果如下。

clear all; clc; close all;
%----------------均匀线列阵实现MUSIC算法------------------%
ang2rad = pi/180;                   % 角度转弧度系数
N = 14;                             % 阵元个数
M = 1;                              % 信源个数
theta = -25.3;                        % 来波方向(角度)
% M = 3;                              % 信源个数
% theta = [-65,0,45];                 % 来波方向(角度)
snr = 20;                           % 信号信噪比dB
K = 512;                            % 总采样点
delta_d = 0.05;                     % 阵元间距
f = 2400;                           % 信号源频率
c = 340;                            % 声速
 
d = 0:delta_d:(N-1)*delta_d;
A = exp(-1i*2*pi*(f/c)*d.'*sin(theta*ang2rad));   % 接收信号方向向量
S = randn(M,K);                     % 阵列接收到来自声源的信号
X = A*S;                            % 最终接收信号，是带有方向向量的信号
X1 = awgn(X,snr,'measured');        % 在信号中添加高斯噪声
Rx = X1*X1'/K;                      % 协方差矩阵
[Ev,D] = eig(Rx);                   % 特征值分解
% [V,D] = eig(A) 返回特征值的对角矩阵 D 和矩阵 V
% 其列是对应的右特征向量，使得 AV = VD
EVA = diag(D)';                     % 将特征值提取为1行
[EVA,I] = sort(EVA);                % 对特征值排序,从小到大。其中I为index：1,2，...，10
EV = fliplr(Ev(:,I));               % 对应特征矢量排序
En = EV(:,M+1:N);                  % 取特征向量矩阵的第M+1到N列特征向量组成噪声子空间
 
% 遍历所有角度，计算空间谱
thetascan = linspace(-90,90,1024);  % 映射到0度到180度
for i = 1:1024
    theta_m = thetascan(i)*ang2rad;
    a = exp(-1i*2*pi*(f/c)*d*sin(theta_m)).';
    p_music(i) = abs(1/(a'*En*En'*a));
end
[p_max,index] = max(p_music);
p_music = 10*log10(p_music/p_max);  % 归一化处理
theta_est = thetascan(index);
est_error = abs(theta_est - theta);
figure()
plot(thetascan,p_music,'b-');hold on;
plot([theta,theta],ylim,'m-.');
grid on;
xlabel('入射角/度');
ylabel('空间谱/dB');
title(['MUSIC测角结果 SNR = ' num2str(snr)]);

3 基于到达时延差估计的定位法

        TDOA（time difference of arrival）是先后估计声源到达不同麦克风的时延差，通过时延来计算距离差，再利用距离差和麦克风阵列的空间几何位置来确定声源的位置。可分为TDOA估计（估计信号到达各麦克风的时间差）和TDOA定位（运用几何关系确定声源位置）两步。

3.1 互相关法

       对于两个观测信号y1(k)、y2(k)之间的互相关函数（CCF，Cross-Correlation Function）定义为

              

        当p=τ时，τ为相对时延，互相关值达到其最大值

        

3.2 广义互相关方法

        广义互相关函数（GCCF，Generalized CCF）与互相关方法相同，但此时两个麦克风之间的TDOA估计可以等效为能够使麦克风输出的滤波信号之间的CCF最大的时间间隔

        

        GCC函数为：

         

        广义互频谱：

        

        互频谱：

        

        这个公式实际应该是CC函数的互相关函数y的傅里叶变换。

        

        Matlab仿真代码及结果如下。

% 互相关测角算法仿真
clear all; clc; close all;

%加载一段声音（matlab自带敲锣声）
load gong;
%采样频率
Fs = 44100;  
%采样周期
dt=1/Fs;
%music_src为声源
music_src=y;       

%设置两个麦克风坐标
mic_d=1;
mic_x=[-mic_d mic_d];
mic_y=[0 0];
plot(mic_x,mic_y,'x');
axis([-15 15 -15 15])
hold on;
quiver(-5,0,10,0,1,'color','black');
quiver(0,-5,0,10,1,'color','black');

%声源位置
r = 10;
theta=25;
s_x=r*cosd(theta);
s_y=r*sind(theta);

plot(s_x,s_y,'o');
xlabel('横轴-x');
ylabel('纵轴-y');
title('声源位置');
quiver(s_x,s_y,-s_x-mic_d,-s_y,1);
quiver(s_x,s_y,-s_x+mic_d,-s_y,1);

%求出距离
dis_s1=sqrt((mic_x(1)-s_x).^2+(mic_y(1)-s_y).^2);
dis_s2=sqrt((mic_x(2)-s_x).^2+(mic_y(2)-s_y).^2);
c=340;
delay=abs((dis_s1-dis_s2)./340);

%设置延时
music_delay = delayseq(music_src,delay,Fs);
figure(2);
subplot(211);
plot(music_src);
axis([0 length(music_src) -2 2]);
title('源信号');
subplot(212);
plot(music_delay);
axis([0 length(music_delay) -2 2]);
title('延时后的信号');

%gccphat算法,matlab自带
% [tau,R,lag] = gccphat(music_delay,music_src,Fs);
% disp(tau);
% figure(3);
% t=1:length(tau);
% plot(lag,real(R(:,1)));

%cc算法
[rcc,lag]=xcorr(music_delay,music_src);
figure(4);
plot(lag/Fs,rcc);
title('互相关函数--cc');
[M,I] = max(abs(rcc));
lagDiff = lag(I);
timeDiff = lagDiff/Fs;
% disp(timeDiff);

%gcc+phat算法，根据公式写
RGCC=fft(rcc);
rgcc=ifft(RGCC*1./abs(RGCC));
figure(5);
plot(lag/Fs,rgcc);
title('广义互相关函数-gcc');
[M,I] = max(abs(rgcc));
lagDiff = lag(I);
timeDiff = lagDiff/Fs;
% disp(timeDiff);


%计算角度,这里假设为平面波
% dis_r=tau*c;
% angel=acos(tau*c./(mic_d*2))*180/pi;
dis_r=timeDiff*c;
theta_est=acos(timeDiff*c./(mic_d*2))*180/pi;
if dis_s1

四、算法对比

       算法在Intel(R) Core(TM) i7-10700 CPU @ 2.90GHz配置的64操作系统上运行，matlab版本为2017a，运行结果如下。

1 DBF仿真结果

        DBF在0~180°范围内搜索1024点，耗时约0.1s，角度平均误差约0.2°。

2 MUSIC算法仿真结果

        MUSIC在0~180°范围内搜索1024点，耗时约1s，角度平均误差约0.03°。

3 互相关算法仿真结果

       互相关函数计算取前1024个点，耗时约0.4s，角度平均误差0.2°。

        对比可以发现，MUSIC算法具有超分辨能力，但运算量大；DBF和GCC没有超分辨能力，但算法相对简单。

4 测距仿真

       远场模型无法测距，这里使用近场模型下的互相关方法估计延时、角度和距离。仿真结果表明距离平均误差很小，但部分位置距离偏差较大，可达约0.5m。

        Matlab仿真代码及结果如下。

% 使用近场模型做角度和距离仿真
clc;clear;close all;

mic1_positon=[-10,0];
mic2_positon=[0,0];
mic3_positon=[10,0];

% 使用实际数据
% [wave,fs] = audioread('myspeech.wav');
% wave = wave(:,1);   %数组第一列
% scale = 0.8/max(wave);
% wave = scale*wave;

% 使用单频仿真数据
f0 = 2000;                                  % 人声频率在500~2000Hz
fs = 44100;                                 % 声音采样率为44100或48000Hz
N = 20000;                                  % 采样点数
t = (1:1:N)'/fs;
wave = cos(2*pi*f0*t);
snr = 20; 
wave = real(awgn(wave,snr));                % 添加噪声
 
Trials = 20;  %测试点的个数
Radius = 15;                 
N = 3;
Sen_position=[mic1_positon;mic2_positon;mic3_positon];
True_position = zeros(Trials, 3);
Est_position = zeros(Trials,3);
Position_error = zeros(Trials,3);
 
% 生成十个随机位置，半径在50以内
for i=1:Trials
    r = rand(1)*Radius;
    t = rand(1)*pi; 
    x = r*cos(t);
    y = r*sin(t);
    True_position(i,1) = x;
    True_position(i,2) =y;    
end
 
%计算距离
Distances = zeros(Trials,N);
for i=1:Trials
    for j=1:N
        x1 = True_position(i,1);
        y1 = True_position(i,2);
        x2 = Sen_position(j,1);
        y2 = Sen_position(j,2);
        Distances(i,j) = sqrt((x1-x2)^2 + (y1-y2)^2 );   
    end
end
TimeDelay = Distances./340.29;
Padding = TimeDelay*44100;  %时延乘采样率  1s的数据的时延，十个数据点，三个MIC
 
for i=1:Trials
   x = True_position(i,1);
   y = True_position(i,2);
   xstr = num2str(round(x));
   ystr = num2str(round(y));
   istr = num2str(i);
   mic1 = [zeros(round(Padding(i,1)),1) ; wave];
   mic2 = [zeros(round(Padding(i,2)),1) ; wave];
   mic3 = [zeros(round(Padding(i,3)),1) ; wave];  %创建一个全零矩阵，矩阵长度为padding，再续上一个wave
   %麦克一开始什么都收不到，经过一定时间的延迟，收到了音频信号
   l1 = length(mic1);
   l2 = length(mic2);
   l3 = length(mic3);
   lenvec = [l1 l2 l3];
   m = max(lenvec);
   c = [m-l1, m-l2, m-l3];
   %找到最远的接受端
   mic1 = [mic1; zeros(c(1),1)];
   mic2 = [mic2; zeros(c(2),1)];
   mic3 = [mic3; zeros(c(3),1)];
   %补零，最近的声音结束了，最远的没有，通过补零让数组都一样长
   
   mic1 = mic1./(Distances(i,1))^2;
   mic2 = mic2./(Distances(i,2))^2;
   mic3 = mic3./(Distances(i,3))^2;
   %声强和距离的关系是平方I = P / (4 * π * r^2)
   multitrack = [mic1, mic2, mic3];
%   wavwrite(multitrack, 44100, name);
 
[x,y] = Locate(Sen_position, multitrack);
Est_position(i,1) = x;
Est_position(i,2) = y;
Position_error(i,1)=abs(Est_position(i,1)-True_position(i,1));
Position_error(i,2)=abs(Est_position(i,2)-True_position(i,2));
end
figure;
plot(True_position(:,1),True_position(:,2),'bd',Est_position(:,1),Est_position(:,2),'r+','LineWidth',2);
legend('True Position','Estimated Position');
xlabel('目标X轴');
ylabel('目标Y轴');
title('TDOA定位估计');
axis([-Radius Radius 0 Radius]);
%越接近0度和180度时误差越大，这是原理上的问题
figure;
subplot(211);
plot(Position_error(:,1));
title('X方向误差');
subplot(212);
plot(Position_error(:,2));
title('Y方向误差');
 
function [x,y] = Locate(Sen_position, multitrack)
s = size(Sen_position);
len = s(1);
timedelayvec = zeros(len,1);
for i=1:len
   timedelayvec(i) = timedelayfunc(multitrack(:,1),multitrack(:,i));
end
t1=timedelayvec(1)-timedelayvec(2);
t2=timedelayvec(3)-timedelayvec(2);
r=(2*(10)^2-340.29^2*(t1^2+t2^2))/(2*340.29*(t1+t2));
a=acos((t1-t2)/20*(340.29^2*(t1+t2)/(2*r)+340.29));
x=r*cos(a);
y=r*sin(a);
end
 
function out = timedelayfunc(x,y)
% suppose sampling rate is 44100
% Let Tx be transit time for x
% Let Ty be transit time for y
% out is Ty - Tx

c = xcorr(x, y);     %互相关函数
[C,I] = max(c);      
out = ((length(c)+1) - I)/44100;
 
end