图论——最短路径之渡河问题

渡河问题是图论（图与网络模型及方法）中求解最短路径的经典例题，也是一道很有意思的问题。

题目大致描述如下：某人带狼、羊、蔬菜渡河，有一艘船，每次渡河人只能载一物。我们都知道，狼吃羊、羊吃菜，所以当人不在场时，狼和羊不能共存、羊和菜不能共存。试述此人的最少渡河次数。

首先第一步，我们将河的两岸分为东西两岸，东岸为起始状态，西岸为最终目标状态。构造一个四维向量，分别代表人、狼、羊、菜的位置状态，1表示在东岸（起始位置），0表示在西岸（目标位置）。利用穷举法我们可以获得所有可以发生的10种情况：

• (1,1,1,1) ——都在东岸
• (1,1,1,0) ——除了菜在西岸，其余都在东岸（以此类推）
• (1,1,0,1)
• (1,0,1,1)
• (1,0,1,0) ——把狼和羊、羊和菜分开，即人和羊在一起，狼和菜在一起
• (0,1,0,1) ——同上
• (0,1,0,0)
• (0,0,1,0)
• (0,0,0,1)
• (0,0,0,0)

上述十种情况分别对应“图”中的十个顶点，本题本质为：求解当初始状态（1,1,1,1）时，经最小次数转移达到最终状态（0,0,0,0）的最短路径。

综上所述，图中的顶点已经构造好，下面要考虑如何确定哪些顶点之间可以有线，而哪些顶点之间不会存在线。

因此第二步，我们需要构造“可行转移“的四维向量。上述十个可行状态，当且仅当对应的两个可行状态之间存在一个可行转移时，两顶点之间才有边，此时我们让存在可行转移的两顶点之间的边对应的权重取1，否则取无穷大（inf）。

定义转移向量（1,0,0,0）、（1,1,0,0）、（1,0,1,0）、（1,0,0,1）分别表示人自己过河、人带狼过河、人带羊过河、人带菜过河。

状态向量与转移向量之间的运算是0+0 = 0；0+1 = 1；1+0 = 1；1+1=0。

即+0表示该物体位置保持不变，+1表示该物体过一次河。观察运算规律，其实本质上是对当前位置状态向量和可行转移操作向量之间进行异或处理，相同留0，不同留1，得到的新的四维向量若属于上述十种可行状态向量，则在先后的两种状态对应的“顶点”之间添加一条边。获得完整的“图”，利用matlab工具箱中的graphshortestpath函数求的最短路径。

具体代码如下：

clc,clear %清空当前命令行窗口和工作区变量
a = [1 1 1 1;1 1 1 0;1 1 0 1;1 0 1 1;1 0 1 0;0 1 0 1;0 1 0 0;0 0 1 0;0 0 0 1;0 0 0 0];%每一行是一个可行状态
b = [1 0 0 0;1 1 0 0;1 0 1 0;1 0 0 1]; %每一行是一个转移状态
w = zeros(10); %邻接矩阵初始化
for i = 1:9
    for j = i+1:10
        for k = 1:4
            if strfind(xor(a(i,:),b(k,:)),a(j,:)) %#ok  
                % strfind(s1,pattern),因此其意思在s1中搜索pattern
                % xor(a,b)表示异或，当两者都是0，或两者是非零值时，xor(a,b)结果为0；否则，xor(a,b)结果为1；
                w(i,j) = 1;
            end
        end
    end
end
w = w';
c = sparse(w); %构造稀疏矩阵
[x,y,z] = graphshortestpath(c,1,10,'Directed',0); %无向图，0/false
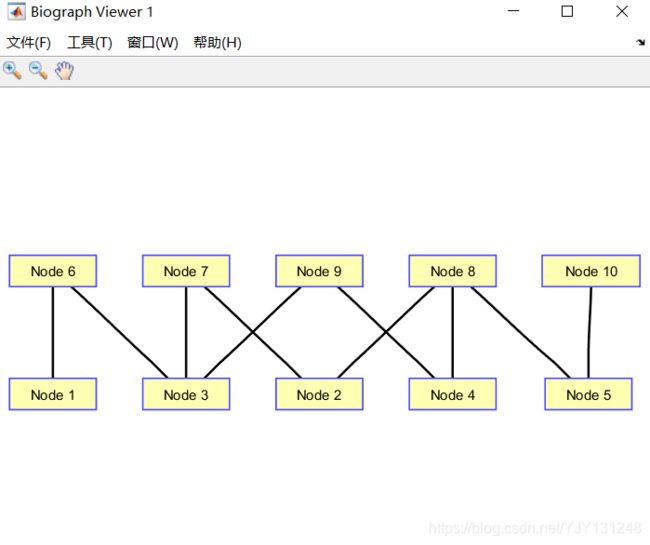
h = view(biograph(c,[],'ShowArrows','off','ShowWeights','off'));  %画出无向图
Edges = getedgesbynodeid(h); %提取句柄h中的边集
set(Edges,'LineColor',[0,0,0]); %为了打印清楚，边画成黑色
set(Edges,'LineWidth',1.5) %线型宽度设置为1.5

在matlab中运行该代码，得到的结果表明的含义如下：

x = 7; %表示最短路径要进行7次渡河
y = 1 6 3 7 2 8 5 10; %表示转移状态顺序：1-6-3-7-2-8-5-10；

图像如下：