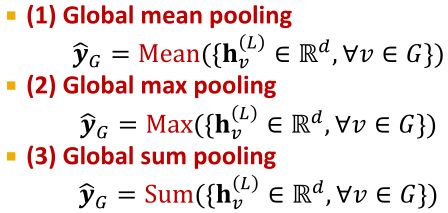《图机器学习》-GNN Augmentation and Training
GNN Augmentation and Training
- 一、Graph Augmentation for GNNs
-
- 1、Feature Augmentation
- 2、Structure augmentation
- 3、Node Neighborhood Sampling
- 二、GNN Training Pipeline
-
- 1、Prediction heads
- 2、Supervised VS Unsupervised
- 3、Loss Function
- 4、Evaluation metrics
- 三、Dataset Split
一、Graph Augmentation for GNNs
之前的假设:
Raw input graph = computational graph,即原始图等于计算图。
现在要打破这个假设,原因如下:
- 如果图过于稀疏:消息传递效率低下
- 如果图过于密集了:消息传递的开销太大
- 如要点击查看某个名人的embedding,要汇聚其成千上万个追随者的信息,这个花销是很大的
- 如果图很大:难以将计算图拟合到CPU内存中
所以,原始输入图不太可能恰好是嵌入的最佳计算图。因此需要Graph Augmentation,改变解构使之适于嵌入。
1、Feature Augmentation
为什么我们需要特征增强?
(1)、输入图没有节点特征;如只有邻接矩阵的时候。
解决方案:
- 为节点分配常量值
如为每个节点都分配一个常数1,在一轮汇聚后,各节点就能学习到其邻居节点的个数。
- 为节点分配唯一的IDs
如为每个节点都分配one-hot编码

该方法每个node的向量不一样,增加了模型的表达能力,但是花费的代价非常大,如one-hot编码的维度和节点数量一致
两种方式的对比:
| Constant node feature | One-hot node feature | |
|---|---|---|
| 表达能力 | 中等。所有的节点都是相同的,但GNN仍然可以从图结构中学习 | 高。每个节点都有唯一的ID,因此可以存储特定于节点的信息 |
| 归纳学习(推广到新的节点) | 高。推广到新节点很简单:我们为它们分配恒定的特征,然后应用我们的GNN | 低。不能泛化到新节点:新节点引入新ID, GNN不知道如何嵌入看不见的ID |
| 计算成本 | 低。只有一维特征 | 高。O(|V|)维度特征,不能应用于大型图 |
| 使用范围 | 任何图 | 小图 |
为什么我们需要特征增强?
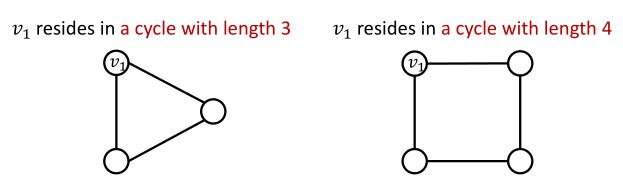
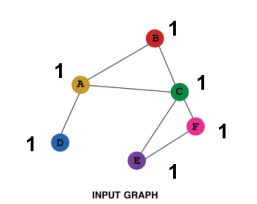
(2)、GNN很难学习某些结构
基于前面的GNN是不能够解答这个问题的,原因是这两个节点的计算图是一样的,学习出来的embedding大致类似
解决方案:
可以添加cycle count作为节点的特征,如下图;即开辟一个特征空间用于描述所需要的属性。

其他常用于数据增强的特征:
- Node degree
- Clustering coefficient
- PageRank
- Centrality
2、Structure augmentation
出发点: Augment sparse graphs(增强稀疏图)
-
Add virtual edges
-
Add virtual nodes
增加一个虚拟节点,虚拟节点将于图中的所有节点相连接
3、Node Neighborhood Sampling
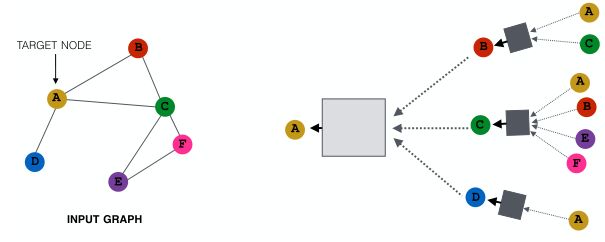
回顾之前的GNN计算图,所有节点都用于消息传递,如下图:
新的想法:
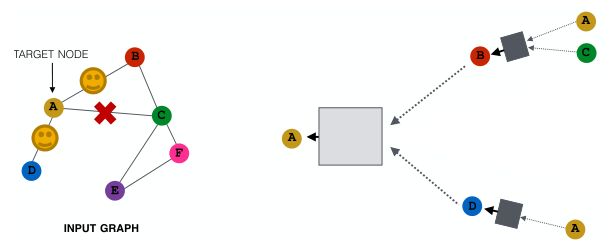
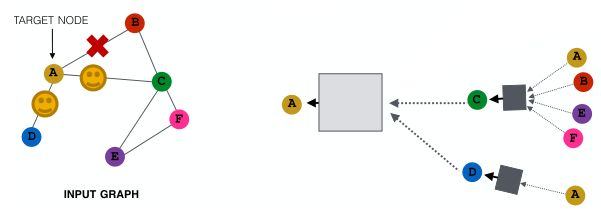
随机的选取邻居节点的子集用于计算图的构建(用于信息传递)
例如,可以在给定的层中随机选择2个邻居来传递消息,如下图:
在大图中,随机采样邻居节点的子集用于信息传递能够减少计算图;但会丢失信息,即获得了效率但失去了一些表现力。
为了弥补,可以在下一层中,当我们计算嵌入时,对不同的邻居进行采样(即每一层都采样不同的邻居用于计算图的构建),提升模型的鲁棒性。
该方法在实践中效果不错。
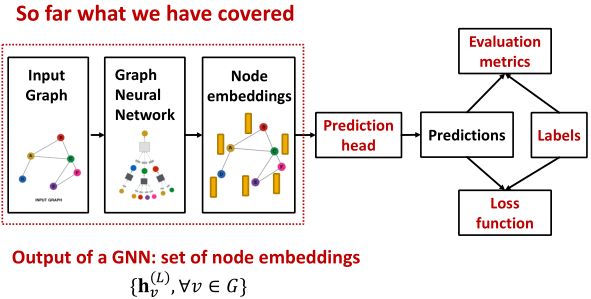
二、GNN Training Pipeline
GNN的训练流水线如下图:
- 设置输入图
- 定义图神经网络架构
- 创建embedding
- 将embedding输入到预测头中
- 对输入做出预测
- 使用Labels定义Loss function
- 反向传播调整参数,改进模型
- 使用指标评估模型
1、Prediction heads
不同的任务级别需要不同的预测头:
- Node-level tasks
- Edge-level tasks
- Graph-level tasks
节点级的预测头:
可以直接使用节点嵌入进行预测。
在GNN计算完后,就获得了各节点的d维的embedding: { h v ( L ) ∈ R d , ∀ v ∈ G } \{h^{(L)}_v∈R^d,∀v ∈ G\} {hv(L)∈Rd,∀v∈G};我们可以使用节点的embedding去做k分类或者回归任务。
如将节点embedding输入到简单的线性层并得到预测结果 y ^ v \hat{y}_v y^v:

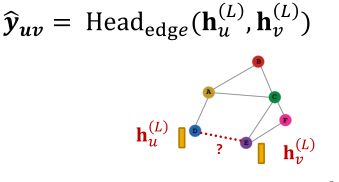
边级的预测头:
使用一对节点嵌入进行预测。
假设我们要预测边 u v uv uv是否存在,可以使用 u u u和 v v v节点的embedding来进行预测,预测结果 y ^ u v \hat{y}_{uv} y^uv:
H e a d e d g e ( h u ( L ) , h v ( L ) ) Head_{edge}(h^{(L)}_u,h^{(L)}_v) Headedge(hu(L),hv(L))的可选项:
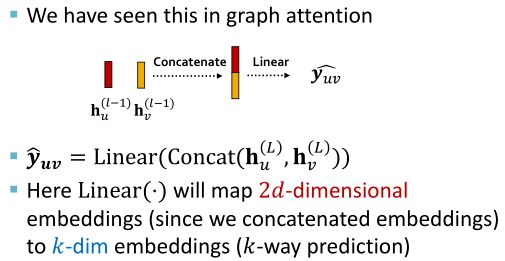
-
Dot product:
y ^ u v = ( h u ( L ) ) T h v ( L ) \hat{y}_{uv}=(h_u^{(L)})^Th_v^{(L)} y^uv=(hu(L))Thv(L)
该公式输出的是一个一维向量,只适用于1-way prediction
若相应用于k-way prediction:
类是于多头注意力机制,创建几个公式分布用于各类的预测:

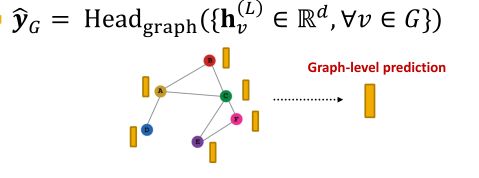
图级别的预测头:
使用图中的所有节点嵌入进行预测。
假设我们现在做的是k分类问题,需要使用图中所有节点的embedding来进行预测:
H e a d g r a p h ( ⋅ ) Head_{graph}(\cdot) Headgraph(⋅)类似于GNN layer中的聚合函数,即先将所有节点进行聚合构建一个代表图的“超级节点”,再使用“超级节点”的embedding来进行预测。
H e a d g r a p h ( h v ( L ) ∈ R d , ∀ v ∈ G ) Head_{graph}(h^{(L)}_v∈R^d, ∀v∈G) Headgraph(hv(L)∈Rd,∀v∈G)的可选项:
这些选项适用于小图形,在一个大图上的全局池将丢失信息。
如,使用一维来表示各节点的embedding,现有两个图 G 1 、 G 2 G_1、G_2 G1、G2的节点embedding表示:
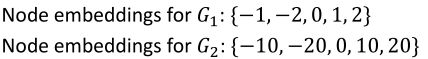
通过node embedding可以看出这两个图具有非常不同的节点嵌入,所以它们的结构应该是不同的。
如果对 G 1 、 G 2 G_1、G_2 G1、G2使用sum pooling:
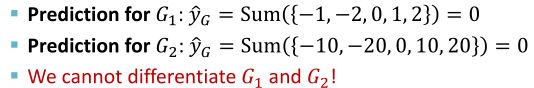
使用sum pooling将无法区分 G 1 G_1 G1和 G 2 G_2 G2。
解决方案:
让我们按层次结构聚合所有节点嵌入,即分层聚合。
如,我们使用 R e L U ( S U M ( ⋅ ) ) ReLU(SUM(\cdot)) ReLU(SUM(⋅))来聚合节点的embedding;
首先分别聚合前2个节点和后3个节点;然后我们再次汇总,做出最终的预测。【不一下聚合所有的节点,分批聚合得到多个结果,再将结果分批聚合】
在 G 1 G_1 G1中,先聚合前两个节点,再聚合后3个节点,再将聚合的结果做聚合; G 2 G_2 G2同理,如下图:

现在我们能够挖掘 G 1 G_1 G1和 G 2 G_2 G2的不同了。
那么先聚合哪些节点呢?如何分层聚合?
我们可以假设图中存在着社区,社区中节点的embedding相似,所以先聚合社区;再将社区聚合的社区聚合成超级社区,不断聚合最后得到一个节点的嵌入;如下图:
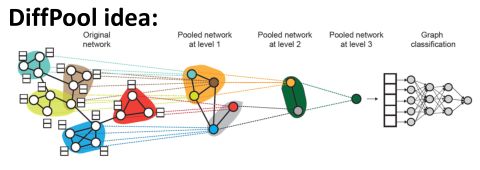
上述可以使用两个GNN来完成:
- GNN A用来计算节点的embedding
- GNN B用来判断节点属于哪个社区,即社区的划分,社区中的所有结点都会聚合为一个结点输入到下一层pooling layer
GNN A和GNN B可以并行执行
2、Supervised VS Unsupervised
- 图的监督学习:
- 标签来自外部;
如预测分子是否有毒的可能性。
- 标签来自外部;
- 图的无监督学习:
- 信号来自于图本身;
如链路预测:预测两个节点是否连通
- 信号来自于图本身;
有时监督与无监督学习之间是模糊的,有时无监督学习也叫“self-supervised”,即无监督学习可以根据数据的结构定义监督任务。
Supervised:
监督学习的标签来自于特定的用例:
- 节点级标签 y v y_v yv:在引用网络中,节点属于哪个学科邻域;
- 边级标签 y u v y_{uv} yuv:在交易网络中,边是否存在欺诈行为
- 图标签 y G y_G yG:在分子图中,是否有毒
再接纳度学习中,将任务归纳为node / edge / graph labels会更好一些,因为会有许多现存的理论框架可以参考和使用。
如,将聚类任务看成是node labels,即每个节点都需要赋予一个类别标签。
Unsupervised:
无监督学习中有时我们只有一个图,没有任何外部标签。
解决方案:
“自监督学习”,可以在图中找到监督信号。
前面的使用PageRank随机生成路径,然后缩小路径上节点embedding的内积就是自监督学习,在图中找到监督信号的例子。
3、Loss Function
如何定义损失函数,我们可以将loss分成两类:
- Classification loss
- Regression loss
接下来根据实际的任务,使用预测标签 y ^ ( i ) \hat{y}^{(i)} y^(i)和实际标签 y ( i ) y^{(i)} y(i)来构建损失函数。
分类任务输出的值是离散的;
回归任务输出值是连续的。
分类任务中,交叉熵(cross entropy, CE)是中常见的损失函数:

对于回归任务,我们经常使用均方误差(MSE),也就是L2 loss:

4、Evaluation metrics
对GNN使用标准的评估指标:
三、Dataset Split
本节讲如何划分数据集为训练集、验证集和测试集。
训练集用于训练模型;
验证机用于调整超参数和各种常量以及决策选择。
- Fixed split:
将对数据集进行一次拆分,分成不相交的三个独立部分,此后一直使用该划分方式。 - Random split:
随机将数据集分为训练/验证/测试集。
模型的性能表现由不同随机分法下的表现的平均。
假设我们想拆分一个图像数据集,每个数据点都是一张图像,这里的数据点是独立的,上述的两种方法会比较好实施。
但对于图数据(graph dataset),每个数据点是一个节点;而图中的数据点是相互连接的,并非独立的。上述两种方法不好实施。
解决方案:
1、 T r a n s d u c t i v e s e t t i n g Transductive\ setting Transductive setting:
保持图结构不变,分割 l a b e l s labels labels。因此在训练集和验证集上使用的都是同一张图。

例子:
- 在训练时,使用整张图的结构信息和1、2节点的标签计算embedding;
- 在验证时,使用整张图的结构信息计算embedding,并在节点3和4的标签上进行评估。
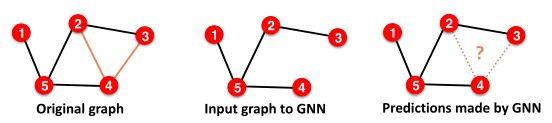
- I n d u c t i v e s e t t i n g Inductive\ setting Inductive setting:
劈开Train/Test/Valid之间的边缘,生成多个独立图。
如下图,虚线边表示去掉的边缘,最后生成三个互相独立的子图。

该方法抛弃了很多图信息,在小图中不推荐该方法,会有结构化信息的泄露。
但该方法能够确保可以泛化到看不见的图上。
例子:
- 在训练时,仅使用节点1和2的图和labels来计算嵌入
- 在验证时,使用节点3和4上的图来计算嵌入,并在节点3和4的标签上进行评估
I n d u c t i v e / T r a n s d u c t i v e Inductive/Transductive Inductive/Transductive对比:
- Transductive:
- 训练/验证/测试集在同一图形上
- 数据集由一个图形组成
- 整个图可以在所有数据集分割中观察到,只分割标签
- 仅适用于节点/边缘预测任务
- Inductive:
- 训练集/验证集/测试集在不同的图上
- 数据集由多个图组成
- 每个分割只能观察分割内的图。一个成功的模型应该推广到看不见的图
- 适用于节点/边/图任务
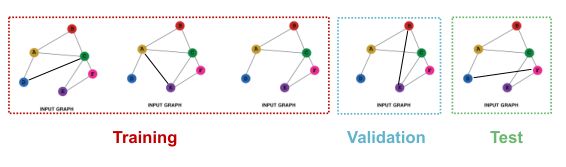
在图级别的分类任务中,每个数据点就是一张图,只适用inductive setting,以图为单位进行划分。
如假设我们有一个5张图的数据集,每个split将包含独立的图:
在连接预测中。
链接预测的目标 : 预测缺失的边
建立链接预测是很棘手的:
- 链接预测是一个无监督/自我监督的任务。需要自己创建标签和数据集分割。
- 具体来说,需要对GNN隐藏一些边,并让GNN预测这些边是否存在
建立连接预测任务:
-
步骤一:在原始图中指定2种类型的边
- Message edges:用于GNN消息传递
- Supervision edges:用于计算目标
图中只保留Message edges,Supervision edges用于监督模型所做的边缘预测,不会被馈送到GNN!
-
将边缘分割为训练/验证/测试
-
方式一:Inductive link prediction split
假设我们有一个包含3个图的数据集。
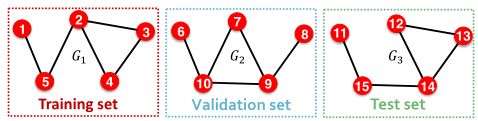
inductive 划分法会将每个图中的边划分为:Message edges+Message edges:

-
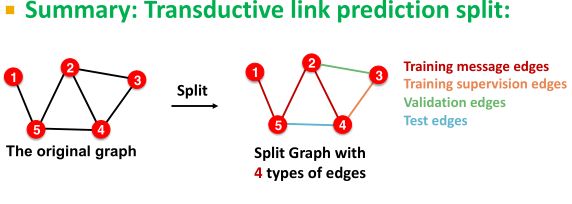
方式二:Transductive link prediction split
(一般在连接任务中默认使用该方式)
假设我们有一个只有1个图的数据集

将边划分为training edges、validation edges、test edges和supervision edges;- 在训练时:训练模型利用training edges预测supervision edges
- 在验证时:使用training edges和supervision edges来validation edges
- 在测试时:利用training edges、supervision edges和validation edges来预测test edges
-