数据结构之二叉排序树(C++实现)
目录
非递归方法:
递归方法:
递归查找:
删除节点
中序遍历:
二叉树是数据结构中的一个非常非常重要的板块,俗话说不到长城非好汉,那么不会二叉树就不算了解数据结构。什么是二叉树,在之前我们了解了链表,但是我们在使用的时候就会发现一个问题就是,链表的每一个节点只能在同一方向指向一个节点,也就是不能分叉,可是在实际应用中必须要有分叉的存在,怎么办呢,前辈们就提出了二叉排序树的概念。通过前边的学习我们了解了单链表有两个区域,就是数据域和指针域,双向链表为了实现反向遍历多加了一个区域叫前驱指针域,所以双向链表就有了三个域,前驱指针域,后继指针域和数据域,同理我们就能猜出来,二叉树又多加了一个域,所以有四个域,即双亲指针域,数据域,左子树指针域,右子树指针域。我们通过下边的图具体了解一下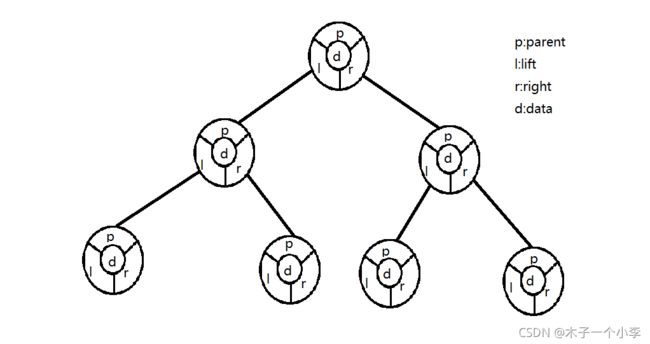
为了便于理解我将排序树的四个区域标记了起来,通过前边的学习我们就可以了解到一点就是,在简历二叉排序树的时候我们需要建立一个结点类,类的属性应该有四点,就是图中的四点,p,l,r,d。那么我们通过节点类一块儿构成了一个树类,所以我们需要建立一个树的类,那么属的类中就没有属性了,因为它的属性就是结点的属性,所以树的行为就是对树的操作,即我们常说的增删改查操作。我们在下边的代码里边详细解释一下。
class node
{
public:
int data;
node *parent;
node *lift;
node *right;
node() : data(-1) , parent(NULL) , lift(NULL) , right(NULL) {}
node(int num) : data(num) , parent(NULL) , lift(NULL) , right(NULL) {}
};上边的代码就是我们建立的结点的类,我们建立了结点的四个区域,以及两个构造函数,也就是说我们在建立一个结点的时候就是创建了一个拥有四个区域的结点,并且通过构造函数可以给其数据域传参数。对于节点类来说,每个结点都有向下的两个指针,并且有一个向上的指针。
class trees
{
public:
trees(int num[] , int len); //构造函数,用来插入n个数据
void insertnode(int data); //非递归的方法
void insertnode1(int data); //递归的方法
node *searchnode(int data); //查找结点
void deletenode(int data); //删除结点及其子树
void inorder(); //中序遍历
private:
void insertnode(node* cur , int data); //递归插入
node *searchnode(node* cur , int data); //递归查找
void deletenode(node* cur); //递归删除
void inorder(node* cur); //递归中序遍历
node* root; //二叉排序树的根节点
};这里的代码就是我们的树的类,构造函数我们利用数组的方法来创建二叉树,我们大家都知道创建二叉树有两种方法,即递归的方法与非递归的方法,所以我在上一次的博文中我为大家讲了什么是递归,并且利用汉诺塔的代码举了例子,并且下边的查找和删除的方法也是利用了递归的方法。
非递归方法:
我们先利用非递归的方法来创建一个二叉树,具体的代码如下:
trees::trees(int num[] , int len)
{
root = new node(num[0]);
for(int i = 1; i p->data)
{
p = p->right;
}
else if(datanew < p->data)
{
p = p-> lift;
}
else if(datanew == p->data)
{
delete newnode;
return;
}
}
newnode->parent = par;
if(par->data > newnode->data)
{
par->lift = newnode;
}
else
{
par->right = newnode;
}
}
/*这个函数主要由两部分组成,一部分是查找,当插入一个
新的节点的时候,程序要知道到底在哪里插入,因为是二叉
排序树,为什么叫二叉排序树,因为左子树的数值一直要比
右子树小,根节点的data一定要比左子树的data大,比右子树的data小。*/ 上边的代码是我们创建一个二叉树并且给其中插入数据,详细的分为以下几步:
1、创建节点,就是node *newnode = new node(int);
2、查找新的节点的具体位置
根据二叉树的性质,给二叉树插入数据的时候需要做一下遍历,如果找到了数据相同的结点,那么新的节点也就没有了存在的意义,所以就将其delete了。
3、找到位置后的插入操作。
上边介绍的就是插入节点的非递归的一个方法,下面来解释一下递归的方法。
递归方法:
什么是递归我就不多说了,想了解的看看我的上一篇博文,递归的方法插入节点其实是我写了一个插入的方法,但是具体的插入操作我写在了私有行为的insertnode方法中,具体的代码如下:
//递归的方法
void trees::insertnode(int data)
{
if(root != NULL)
{
insertnode(root , data); //调用递归插入的方法
}
}
void trees::insertnode(node* cur , int data)
{
//首先要查看插入的数据和当前结点的data的大小
if(data < cur->data)
{
if(cur->lift == NULL)
{
cur->lift = new node(data);
cur->lift->parent = cur;
}
else
{
insertnode(cur->lift , data); //这里就进入递归了,因为一个结点的左子树单独来看也是一个二叉树
}
}
else if(data>cur->data)
{
if(cur->right == NULL)
{
cur->right = new node(data);
cur->right->parent = cur;
}
else
{
insertnode(cur->right , data);
}
}
return;
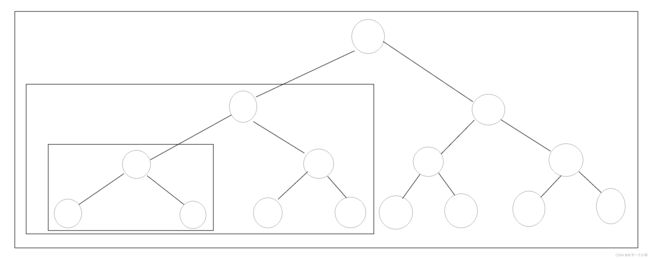
}看上边的代码可能有很多人不理解到底是怎么一个递归的调用,我用一张图来做一下解释,应该就能懂了
如图所示,每一个框都可以看做是一个二叉树,那么也就是说对二叉树的所有操作它都可以进行,所以就有了递归的方法进行操作,那么我们对私有属性的函数insertnode执行的步骤进行解释:
1、如果当前的节点的数据值小于data,那么我们应该在它的左子树进行插入操作,此时就有了一个判断,就是说如果当前节点没有左子节点,那么我们就把插入的新节点作为它的左子节点,否则的话那它的左子节点再和data作比较,一直进行下去,直到截至。
2、如果当前结点的数据值大于data的情况,其实和第一步差不多,就是一左一右,一大一小而已,我就不多废话了,主要是懒。
我们再来看看在二叉树里边的查找的方法:
递归查找:
通过上边的代码和上一篇的博客我们了解到了递归算法的使用可以使我们的代码变的更为简单,代码也不再冗余,那么我们的查找也是用递归的方法来写,代码如下:
//以下是查找
node* trees::searchnode(int data)
{
node * p = new node(data);
if(root != NULL)
{
p = searchnode(root , data);
return p;
}
return NULL;
}
node* trees::searchnode(node* cur , int data)
{
if(data < cur->data)
{
if(cur->lift == NULL)
{
return NULL;
}
return searchnode(cur->lift , data);
}
else if(data>cur->data)
{
if(cur->right == NULL)
{
return NULL;
}
return searchnode(cur->right , data);
}
return cur;
}
通过上边的代码我们可以总结出来实现二叉排序树的查找过程可以分为以下几步:
1、如果data小于当前的cur的值,且cur的左子树存在,则继续搜索cur的左子树,否则返回NULL;
2、如果data大于当前的cur的值,且cur的右子树存在,则继续搜索cur的右子树,否则返回NULL;
3、如果data等于当前结点的值,则返回cur。
删除节点
在实际的工作当中我们经常会遇到星空删除树中数据的情况,所以我们必须要有一个完整的算法来实现删除操作,所谓的删除当然了,我这里直接就把定位节点后的树给删除了,要想之删除一个数据我觉得是可以的,只是我在写我的代码的时候并没有去写它,因为牵扯到再次比较大小,重新排序等太麻烦了,现在我们就直接把树给删除的代码给大家看看吧
//以下是删除
void trees::deletenode(int data)
{
node* cur = new node(data);
cur = searchnode(data);
if(cur != NULL)
{
deletenode(cur);
}
}
void trees::deletenode(node *cur)
{
if(cur->lift != NULL)
{
deletenode(cur->lift);
}
if(cur->right != NULL)
{
deletenode(cur->right);
}
if(cur->parent == NULL)
{
delete cur;
root = NULL;
return;
}
if(cur->parent->data > cur->data)
{
cur->parent->lift = NULL;
}
else
{
cur->parent->right = NULL;
}
delete cur;
}针对以上代码我在这里做以下解释:
public成员方法deletenode()删除数据为data的结点及其子树。首先调用了searchnode()方法来查找到我们需要删除的结点位置,,如果找到了就会调用私用的成员方法searchnode()进行返回。
private成员方法也是使用的是递归的方法进行删除的具体的方法如下
1、如果cur左子树存在,则递归删除左子树;
2、如果其右子树存在,则递归删除右子树;
3、如果最后删除粗人,此时cur是根节点,则需要把root置空,否则的话就把其父节点对应的指针置空。
那么到这里为止啊,我们的二叉树第一座大山“入门山”已经翻过去了,我们可以写一个打印函数进行打印,和链表一样,要想打印必须遍历,在二叉树中的遍历方法我下一篇博客再详细介绍,这里就直接使用中序遍历吧。
中序遍历:
这一段不需要看懂,其实也很简单啦,下篇博客我做详细的解释
//中序遍历
void trees::inorder()
{
if(root == NULL)
{
return;
}
inorder(root);
}
void trees::inorder(node* cur)
{
if(cur != NULL)
{
inorder(cur->lift);
cout<data<<" ";
inorder(cur->right);
}
} 好的,到此为止基本上就写完了,我们加入主函数来看看运行的效果是怎样的:
int main()
{
int num[] = {5,3,1,4,8,9,7,6,2,11,34,99,100};
trees tr(num , 13);
tr.inorder();
cout << endl;
tr.insertnode(78);
tr.inorder();
cout << endl;
tr.deletenode(11);
tr.inorder();
return 0;
}ok,今天的二叉树就先介绍到这里,下一期博客我们说一下二叉树的几种排序方式,最后把我们的工程代码贴上以供参考,如有问题欢迎留言或私信讨论
//main.cpp
#include "tree.h"
int main()
{
int num[] = {5,3,1,4,8,9,7,6,2,11,34,99,100};
trees tr(num , 13);
tr.inorder();
cout << endl;
tr.insertnode(78);
tr.inorder();
cout << endl;
tr.deletenode(11);
tr.inorder();
return 0;
}//tree.h
#ifndef _TREE_H_
#define _TREE_H_
#include
using namespace std;
class node
{
public:
int data;
node *parent;
node *lift;
node *right;
node() : data(-1) , parent(NULL) , lift(NULL) , right(NULL) {}
node(int num) : data(num) , parent(NULL) , lift(NULL) , right(NULL) {}
};
class trees
{
public:
trees(int num[] , int len); //构造函数,用来插入n个数据
void insertnode(int data); //非递归的方法
void insertnode1(int data); //递归的方法
node *searchnode(int data); //查找结点
void deletenode(int data); //删除结点及其子树
void inorder(); //中序遍历
private:
void insertnode(node* cur , int data); //递归插入
node *searchnode(node* cur , int data); //递归查找
void deletenode(node* cur); //递归删除
void inorder(node* cur); //递归中序遍历
node* root; //二叉排序树的根节点
};
#endif //tree.cpp
#include "tree.h"
trees::trees(int num[] , int len)
{
root = new node(num[0]);
for(int i = 1; i p->data)
{
p = p->right;
}
else if(datanew < p->data)
{
p = p-> lift;
}
else if(datanew == p->data)
{
delete newnode;
return;
}
}
newnode->parent = par;
if(par->data > newnode->data)
{
par->lift = newnode;
}
else
{
par->right = newnode;
}
}
//递归的方法
void trees::insertnode(int data)
{
if(root != NULL)
{
insertnode(root , data); //调用递归插入的方法
}
}
void trees::insertnode(node* cur , int data)
{
//首先要查看插入的数据和当前结点的data的大小
if(data < cur->data)
{
if(cur->lift == NULL)
{
cur->lift = new node(data);
cur->lift->parent = cur;
}
else
{
insertnode(cur->lift , data); //这里就进入递归了,因为一个结点的左子树单独来看也是一个二叉树
}
}
else if(data>cur->data)
{
if(cur->right == NULL)
{
cur->right = new node(data);
cur->right->parent = cur;
}
else
{
insertnode(cur->right , data);
}
}
return;
}
//以下是查找
node* trees::searchnode(int data)
{
node *p = new node(data);
if(root != NULL)
{
p = searchnode(root , data);
return p;
}
return NULL;
}
node* trees::searchnode(node* cur , int data)
{
if(data < cur->data)
{
if(cur->lift == NULL)
{
return NULL;
}
return searchnode(cur->lift , data);
}
else if(data>cur->data)
{
if(cur->right == NULL)
{
return NULL;
}
return searchnode(cur->right , data);
}
return cur;
}
//以下是删除
void trees::deletenode(int data)
{
node* cur = new node(data);
cur = searchnode(data);
if(cur != NULL)
{
deletenode(cur);
}
}
void trees::deletenode(node *cur)
{
if(cur->lift != NULL)
{
deletenode(cur->lift);
}
if(cur->right != NULL)
{
deletenode(cur->right);
}
if(cur->parent == NULL)
{
delete cur;
root = NULL;
return;
}
if(cur->parent->data > cur->data)
{
cur->parent->lift = NULL;
}
else
{
cur->parent->right = NULL;
}
delete cur;
}
//中序遍历
void trees::inorder()
{
if(root == NULL)
{
return;
}
inorder(root);
}
void trees::inorder(node* cur)
{
if(cur != NULL)
{
inorder(cur->lift);
cout<data<<" ";
inorder(cur->right);
}
}