【初中生讲机器学习】3. 支持向量机(SVM)一万字详解!超全超详细超易懂!
创建时间:2024-01-31
最后编辑时间:2024-02-01
作者:Geeker_LStar
你好呀~这里是 Geeker_LStar 的人工智能学习专栏,很高兴遇见你~
我是 Geeker_LStar,一名初三学生,热爱计算机和数学,我们一起加油~!
⭐(●’◡’●) ⭐
那就让我们开始吧!
文章目录
- 一、基础概念
-
- 1. 向量
- 2. 支持向量
- 3. 超平面
- 4. 间隔
- 二、数学推导(原理)
-
- 1. 线性可分支持向量机
- 2. 软间隔支持向量机
- 3. 非线性支持向量机
上一篇中,我对监督学习以及其中的各种算法做了大致的说明。我打算先从分类算法学起,因为最好奇 SVM,所以第一个就是支持向量机(SVM)啦嘿嘿。
支持向量机,英文全称 Support Vector Machine,简称 SVM。是二分类算法的一种,常常用于图像、文字等的分类。我在下一篇文章中会利用支持向量机识别(不同种类的)鸢尾花图像。
一、基础概念
为了深入理解支持向量机,我们首先需要理解一些数学概念。
它们包括:向量、支持向量、超平面、间隔
1. 向量
Well,向量肯定大家都不陌生。从数学或物理角度来看,“向量”是指有向线段,不过从数据科学领域来看,“向量”通常指的是某样本的特征表示。举个例子,我们要统计某班同学的身高体重并分析一些情况,有下表:
| 姓名 | 性别 | 身高/cm | 体重/kg |
|---|---|---|---|
| A | 男 | 175 | 70 |
| B | 女 | 165 | 55 |
好吧,但是计算机不认识这种表示,为了让计算机能够理解,我们让 1 代表男生,0 代表女生(姓名对于这个数据分析的例子来说并不重要),那么,一个身高 175cm,体重 70kg 的男生就可以表示为:[1, 175, 70]。这样才能更好地交给计算机处理。
说白了就是特征向量嘛。
正常来讲,男生的数据和女生的数据差别还是比较明显的(尤其是如果以身高作为主成分来看的时候),如果画出图,数据的分布应该会像下图,分明的两堆(或许“两坨”会更形象一点?)。
ok,现在图已经有了,SVM 的任务(简单且不太严谨地概括一下)就是找到一个超平面(后面会讲,这张图里就是一条线),把这两坨数据分开,并且这个超平面到支持向量的距离之和需要最大。
我知道肯定有些童鞋和我曾经 n 次一样看到这里就开始一头雾水了()()不过没事,咱慢慢来嘛。
2. 支持向量
所以,这个突然冒出来的“支持向量”是什么东西?
weeeeell,先接着上面的图聊,划分这两坨数据,有 n 种划分方式,比如图中已经画出的 H1、H2、H3,但是从考虑到模型的泛化能力(就是分类器对从来没见过的新数据的分类能力),H1 和 H2 肯定不如 H3 好。
(为什么?首先 H1 肯定不用说了,连已有数据都分错了,H2 太过靠近两坨数据的边界,在新数据上的表现不会很好)
但是对于 H3,新的问题又来了,这好像有无数种分法。。。
哪一种最好?(好 ≈ 对新数据的分类能力强)
直观来看,分割线(超平面)肯定不能距离某一个数据点特别近,否则就会和之前提到过的 H2 线一样,“冗余空间” 太小,导致泛化能力不强。
还是直观来看,怎么让这个 “冗余空间” 变大一些呢?
——让这个分割线更靠近两个不同类的数据点之间呀,更加均衡一些!(就是不要太偏心(((
换一种比较严谨的说法就是:让距离决策超平面最近的两个不同类的向量(样本)到超平面的距离(都)尽可能大。(如果你还在上初中高中,你可能会觉得这种表述很熟悉——“求某函数最小值的最大值”,或者,均值不等式?(doge))
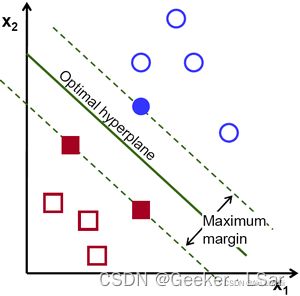
其中,这 “两个不同类的向量(正负样本)” 就是支持向量。如下图中的红色实心方块和蓝色实心圆。and 绿色实线就是(这个例子中)最合适的超平面。
更严谨一点,各类别向量空间中到决策超平面最近的正负样本称为支持向量。
不过,需要先说明,一开始我们并不知道哪两个向量会成为支持向量,支持向量的选取和决策超平面的选取是同时进行的,下面还会再讲到~

好好好我知道有些童鞋已经着急了,说了这么半天超平面到底是个啥?
别急,马上启动()
3. 超平面
还是从简单的例子开始。
要把二维空间划分为两部分,需要一条直线(一维);要把三维空间划分为两部分,需要一个平面(二维)。那如果要把三维以上的空间划分为两部分怎么办呢?没错,这个时候就需要一个超平面。
超平面的数学定义(我是说文字表述)并不难理解:超平面是 n 维欧氏空间中余维度等于一的线性子空间,也就是必须是 (n-1) 维度。这是平面中的直线、空间中的平面之推广(n>3 才被称为 “超” 平面)。
well,虽然从上面这几行来看,理解什么是超平面似乎并不难,但真要通过严格的数学证明去更本质地理解它也真的不简单,来看看。
先来看超平面的数学定义式:
W T X + b = 0 W^{T} X+b=0 WTX+b=0其中 W 和 X 都是 n 维的列向量,W 是法向量,X 是超平面上的点,W 和 X 决定了超平面的方向。T 表示转置,b 是一个常数。
浅举例一下,比如一个三维坐标系中的二维平面,上面有一个向量 A B ⃗ \vec{AB} AB,其中 A = ( x 0 , y 0 , z 0 ) , B = ( x , y , z ) A=(x0, y0, z0),B=(x, y, z) A=(x0,y0,z0),B=(x,y,z),显然 A B ⃗ = ( x − x 0 , y − y 0 , z − z 0 ) \vec{AB}=(x-x0, y-y0, z-z0) AB=(x−x0,y−y0,z−z0),还有一个法向量 M N ⃗ \vec{MN} MN(垂直于二维平面的向量),比如坐标 ( A , B , C ) (A, B, C) (A,B,C),由向量数量积的知识可知, A B ⃗ ⋅ M N ⃗ = 0 \vec{AB}·\vec{MN} = 0 AB⋅MN=0,也就是:
A ( x − x 0 ) + B ( y − y 0 ) + C ( z − z 0 ) = 0 A(x-x0)+B(y-y0)+C(z-z0) = 0 A(x−x0)+B(y−y0)+C(z−z0)=0再把这个式子展开并移项,就得到: A x + B y + C z = A x 0 + B y 0 + C z 0 Ax+By+Cz = Ax0+By0+Cz0 Ax+By+Cz=Ax0+By0+Cz0令右边等于常数 b,再把 ABC 换成 w1、w2、w3,xyz 换成 x1、x2、x3(这样方便推广)就有: w 1 x 1 + w 2 x 2 + w 3 x 3 = b w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3} = b w1x1+w2x2+w3x3=b这实际上就是二维平面的方程,把这个式子推广到 n 维,就得到 n 维下的超平面的方程:
w 1 x 1 + w 2 x 2 + . . . + w n x n = b w_{1}x_{1}+w_{2}x_{2}+...+w_{n}x_{n} = b w1x1+w2x2+...+wnxn=b把所有 w 和 x 用向量表示,不就得到超平面的定义式了嘛! W T X + b = 0 W^{T} X+b=0 WTX+b=0呃当然 b 似乎需要变个号,但那不重要,b 只是一个常数。
既然提到了法向量,顺带说一下超平面的正反吧,这样对于理解后面的内容会更容易:
一个超平面可以把它所在的空间分为两部分,其中它的法向量指向的一面是超平面的正面,另一面是超平面的反面。
相应的,有:
{ W T X + b > 0 ,正面 W T X + b = 0 ,超平面上 W T X + b < 0 ,反面 \left\{\begin{matrix}W^{T}X+b > 0,正面 \\W^{T}X+b = 0,超平面上 \\W^{T}X+b < 0,反面 \end{matrix}\right. ⎩ ⎨ ⎧WTX+b>0,正面WTX+b=0,超平面上WTX+b<0,反面
ok,这样对于超平面的理解应该会更深入一层!(我当时看了半个晚上)
4. 间隔
讲完超平面,间隔也是一个很重要的概念。
假设现在我们找到了一个决策超平面,把所有数据点分为两堆,那对于每一个数据点,这个分法的可信度(正确性)有多少?
很明显,一个点离超平面越远,那么它被分类正确的可能就越大(如果这个点在超平面的旁边,它通常是特征不那么鲜明的,可能被分错的),在已知超平面为 W T X + b = 0 W^{T} X+b=0 WTX+b=0 的情况下,点到超平面的距离大小可以用 ∣ W T X + b ∣ |W^{T} X+b| ∣WTX+b∣ 判断, ∣ W T X + b ∣ |W^{T} X+b| ∣WTX+b∣ 越大,说明点到超平面的距离越远。
如果不好理解,可以这么想:超平面 W T X + b = 0 W^{T} X+b = 0 WTX+b=0 是一个基准面,某个点在和超平面平行的另一个平面上,这个面的方程是 W T X + b = C W^{T} X+b = C WTX+b=C,C 就是相对于基准面的偏移量大小,也就是 ∣ W T X + b ∣ |W^{T} X+b| ∣WTX+b∣,这个值越大,说明点距离超平面的偏移量越大,也就是点到超平面的距离越远。
那么,如果我想同时判断一个点是否分类正确 and 可信度有多少,怎么办?
这时,我们需要引入一个符号变量。好巧不巧,分类结果(或者说标签) y ∈ 1 , − 1 y∈{1, -1} y∈1,−1。也就是说,如果一个变量落在超平面的正面,那么它的标签就是 +1,如果落在超平面的反面,它的标签就是 -1,如下图。

不难发现,如果分类正确, y y y 的符号和 W T X + b W^{T} X+b WTX+b 是一致的,也就是 y ⋅ ( W T X + b ) y · (W^{T} X+b) y⋅(WTX+b) 是正数,利用这一点可以判断分类是否正确。并且由于 ∣ y ∣ = 1 |y| = 1 ∣y∣=1,所以 y ⋅ ( W T X + b ) y · (W^{T} X+b) y⋅(WTX+b) 的大小等于 ∣ W T X + b ∣ |W^{T} X+b| ∣WTX+b∣ 的大小,利用这一点可以得出点距离超平面的距离,进而判断分类的可信度。
y ⋅ ( W T X + b ) y · (W^{T} X+b) y⋅(WTX+b) 就是函数间隔。
上文说,要让支持向量到超平面的距离尽可能大,这个“距离”指的是函数间隔吗?并不是,这其中的原因在于,如果等比例改变 W W W 和 b b b,根据向量数乘的知识,超平面本身是不会变的,但是函数间隔却会等比例增加。所以,“让函数间隔最大” 的结果就是函数间隔有可能趋向正无穷。
为此,我们可以在函数间隔的基础上除以一个量,使得新的这一种间隔不会随着 W W W 和 b b b 的改变而等比例改变,比如,下面这种间隔就符合要求:
∣ W T X + b ∣ ∣ ∣ W ∣ ∣ \frac{|W^{T}X+b|}{||W|| } ∣∣W∣∣∣WTX+b∣
这个间隔被称为几何间隔,这里只是以一种比较好理解的方式提出它,至于它为什么是这个式子,下一部分会给出详细的解释~
上面提到的 “到超平面的距离尽可能大” 其实就是 “几何间隔尽可能大”。
以上四个小部分就当作热身吧,SVM 最精髓的部分马上开始!
二、数学推导(原理)
先说嗷:我目前仅有一部分高中数学和更少更少一部分高等数学的基础,所以这一部分有任何 bug 请各位童鞋 and 大佬尽情拷打我(((
支持向量机分为三种:线性可分支持向量机、软间隔支持向量机、非线性支持向量机。(关于线性和非线性、线性可分和线性不可分,之前的文章中解释过啦~)
其中第一种最简单,利用硬间隔最大化,第二种利用软间隔最大化,第三种利用核函数+软间隔最大化(这些名词后面都会解释哒)。先从第一种开始推吧~
1. 线性可分支持向量机
书接上文,SVM 的核心是什么?
——让距离决策超平面最近的两个不同类的向量(样本)到超平面的间隔尽可能大。
(其实总觉得这句话并不绝对严谨,但是这样会更容易理解,并且在一定程度上也是严谨的(天a我在绕什么))((
我们现在已经得到了超平面的方程,接上文,为了确定距离等一堆量(下面会一个一个说),并且找到最优超平面,我们还需要知道正负超平面的方程,然后进行一些向量运算…
注意注意,“正超平面”和“超平面的正面”并不是同一个东西(没错的确有点emmm难说),“正超平面”是指,通过正样本支持向量并且和决策超平面平行的超平面,负超平面同理。
根据超平面的方程,有:
{ W T X + b = C ,正超平面的方程 W T X + b = − C ,负超平面的方程 \left\{\begin{matrix}W^{T}X+b = C,正超平面的方程 \\W^{T}X+b = -C,负超平面的方程 \end{matrix}\right. {WTX+b=C,正超平面的方程WTX+b=−C,负超平面的方程因为正负超平面都和决策超平面平行,所以只需要上下平移即可,±C 是平移量。前面说过正负超平面到决策超平面的距离要均衡,所以一个 +C 一个 -C 也不难理解~
化简,两边同时除以 C,得到:
(向量数乘法则告诉我们,同比例放缩并不会改变这个超平面(上面也有提到过),这里让函数间隔为 1 只是为了计算方便,实际上它是多少都行)
{ W T X + b = 1 ,正超平面的方程 W T X + b = − 1 ,负超平面的方程 \left\{\begin{matrix}W^{T}X+b = 1,正超平面的方程 \\W^{T}X+b = -1,负超平面的方程 \end{matrix}\right. {WTX+b=1,正超平面的方程WTX+b=−1,负超平面的方程或者说:
W T X + b = ± 1 W^{T}X+b = ±1 WTX+b=±1
然后计算两个支持向量(在正负超平面上)到决策超平面的距离,二维空间中,点到直线的距离公式是:
∣ A x 0 + B y 0 + C A 2 + B 2 ∣ \left | \frac{Ax_{0}+By_{0}+C}{\sqrt{A^{2}+B^{2} } } \right | A2+B2Ax0+By0+C
对没错,其实就是:直线的方程除以向量的范数(二维空间内),超级智障((
(模长和范数可以认为是同一个东西,都表示向量的长度。空间几何里喜欢用模长,线性代数里更爱用范数。)
插播一句,一年多前我手推这个公式,费了老大劲了(当时还没学向量之类的),现在一眼看出“套路”(((
Ok,推广到 n 维,n 维下超平面的方程我们已经知道了,n 维向量(就是我们要用到的支持向量)的范数和二维的也是一个套路,把 n 个分量的平方加起来再开方。
所以,n 维空间下支持向量(X)到超平面的距离公式不就这个嘛!其实就是之前提到的,几何间隔:
∣ W T X + b ∣ ∣ ∣ W ∣ ∣ \frac{|W^{T}X+b|}{||W|| } ∣∣W∣∣∣WTX+b∣ 其中 ∣ ∣ W ∣ ∣ = w 1 2 + w 2 2 + . . . + w n 2 , W T X = w 1 x 1 + w 2 x 2 + . . . + w n x n 其中||W||=\sqrt{w_{1}^2+w_{2}^2+...+w_{n}^2} ,W^{T}X = w_{1}x_{1}+w_{2}x_{2}+...+w_{n}x_{n} 其中∣∣W∣∣=w12+w22+...+wn2,WTX=w1x1+w2x2+...+wnxn
由之前对于正负超平面方程的推导可得,公式的分母等于 1,所以,其中一个支持向量到决策超平面的距离是:
r = 1 ∣ ∣ W ∣ ∣ r = \frac{1}{||W||} r=∣∣W∣∣1那么正负超平面之间的距离(间隔)就是 2 r = 2 ∣ ∣ W ∣ ∣ 2r = \frac{2}{||W||} 2r=∣∣W∣∣2
线性可分 SVM 中的间隔也被称为硬间隔。
转化为图:
我们要求的就是 2 r 2r 2r 的最大值,可以转换为求 ∣ ∣ W ∣ ∣ 2 \frac{||W||}{2} 2∣∣W∣∣ 的最小值。进一步,转化成求 ∣ ∣ W ∣ ∣ 2 2 \frac{||W||^{2}}{2} 2∣∣W∣∣2 的最小值。
好,现在推导过程中最核心的内容已经搞定!(又变成了熟悉的(我是说初高中生熟悉的)函数最值问题,不过这个问题貌似没有那么简单…)
well,我们似乎还漏了一个约束条件——上面一直没有提到分类结果。
分类结果好办,两类样本,正样本的分类结果就是 +1,负样本的分类结果就是 -1 嘛。数学表示就是:
{ W T X + b ≥ 1 , y = 1 W T X + b ≤ − 1 , y = − 1 \left\{\begin{matrix}W^{T}X+b ≥ 1,y = 1 \\W^{T}X+b ≤ -1,y = -1 \end{matrix}\right. {WTX+b≥1,y=1WTX+b≤−1,y=−1
再把两边相乘(也就是函数间隔大于等于 1),最后,问题被转化为一个在约束条件下求函数最小值的问题,即(还是都换成小写吧,看着舒服点emm):
{ m i n ∣ ∣ w ∣ ∣ 2 2 y i [ w t x + b ] ≥ 1 , i = 1 , 2... n \left\{\begin{matrix}min \frac{||w||^{2}}{2} \\y_{i}[w^{t}x+b] ≥ 1,i = 1, 2...n \end{matrix}\right. {min2∣∣w∣∣2yi[wtx+b]≥1,i=1,2...n
好,以上就是 SVM 的核心原理,式子已经推导完了,下面要解决的就是怎么计算的问题了…(记住这一部分讲的是线性可分支持向量机噢~)
好吧,如果没有下面那个约束条件的式子,直接导数或者偏导启动,奈何支持向量机要考虑约束条件(((
嗯,变量受到约束条件的限制,求函数极值,这是个凸二次规划问题,那就拉格朗日乘数法启动吧(((嗯反正都是启动(doge)
摘自百度:这种方法将一个有 n 个变量与 k 个约束条件的最优化问题转换为一个有 n + k 个变量的方程组的极值问题,其变量不受任何约束。这种方法引入了一种新的标量未知数,即拉格朗日乘数:约束方程的梯度(gradient)的线性组合里每个向量的系数。此方法的证明牵涉到偏微分,全微分或链法,从而找到能让设出的隐函数的微分为零的未知数的值。
eeee看着好吓人。。。不过没事,因为我们需要计算的例子里面只涉及到一个变量和一个约束条件,所以相对。。。呃好吧相对也不简单。
推导过程是这样的,我真的没有能力解释了()。大概就是用拉格朗日乘子法和对偶,然后变成常规的没有约束条件的求最值问题,再用偏导。不过。。。我可以说我真的明白的只有偏导。。。。。。
2. 软间隔支持向量机
好好好终于讲完线性可分了,别人用高数消愁,我被高数变成消愁()
为什么会想到软间隔 SVM 呢?先来看个图:
还是最开始提到的通过身高体重数据区分男生女生的例子,在第一部分中我们画出的图其实非常理想化,所有数据都被 “正好” 分成两堆。但是这种情况在现实生活中很少见。就比如,有一些男生比较矮,有一些女生比较高,所以真实的数据更可能像下图这样分布:

换言之,从整体来看,数据集还是大致呈现线性可分(近似线性可分)的样子的,但是存在一些不按常理出牌的点(特异点、异常值),导致数据集变成线性不可分的了(或者说近似线性可分的)。特异点的数学表达就是不满足函数间隔大于等于 1 的约束条件,即不满足 y i [ w t x + b ] ≥ 1 , i = 1 , 2... n y_{i}[w^{t}x+b] ≥ 1,i = 1, 2...n yi[wtx+b]≥1,i=1,2...n。
这怎么办呢?——既然做不到完美地分开两坨数据,那就适当放宽条件嘛!
我们引入一个松弛变量 ξ i ξi ξi(就相当于一个“容忍区间”),然后让这些特异点的函数间隔加上松弛变量 ξ i ξi ξi 之后满足大于等于 1,就可以了。数学表达: y i [ w t x + b ] + ξ i ≥ 1 , i = 1 , 2... n y_{i}[w^{t}x+b]+ ξi ≥ 1,i = 1, 2...n yi[wtx+b]+ξi≥1,i=1,2...n
在线性不可分 SVM 中的间隔,就是软间隔(挺形象的,有一定容忍度的间隔嘛)。
当然,引入松弛变量也是要付出代价的,这个代价表现在目标函数上。
对于线性可分 SVM,我们需要令 ∣ ∣ w ∣ ∣ 2 2 \frac{||w||^{2}}{2} 2∣∣w∣∣2 最小,但是在软间隔 SVM 中,我们引入了松弛变量,并且很明显,考虑到分类器的性能,这个 “容忍度” 并不能太大(也就是松弛变量也要尽可能小),所以,我们的目标函数变为:
1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i n ξ i \frac 1 2 ||w||^2 + C \sum_i^n \xi _i 21∣∣w∣∣2+Ci∑nξi这就是一个在原先的基础上加上了和松弛变量有关的求和函数的目标函数,其中 C C C 是惩罚项,我们需要令目标函数最小。
然后,其实现在问题的本质已经解决了,不过就是:
{ 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i n ξ i (目标函数,最小) y i [ w t x + b ] + ξ i ≥ 1 , i = 1 , 2... n (约束条件) \left\{\begin{matrix}\frac 1 2 ||w||^2 + C \sum_i^n \xi _i(目标函数,最小) \\y_{i}[w^{t}x+b]+ ξi ≥ 1,i = 1, 2...n(约束条件) \end{matrix}\right. {21∣∣w∣∣2+C∑inξi(目标函数,最小)yi[wtx+b]+ξi≥1,i=1,2...n(约束条件)
接下来就是令人emmm的数学推导过程了,和线性可分 SVM 是完全一样的,还是用拉格朗日乘子法和对偶和偏导去解决就 ok(怎么说的好像我很会一样emm)。
发现了吗?软间隔 SVM 的原理其实和线性可分 SVM 很像很像,不过就是多了一个松弛变量。so 如果理解了线性可分 SVM 的原理(当然,可以不包括那一大坨令人emm的数学推导。。),理解线性不可分 SVM 并不难。
喔cool!线性已经搞定了,接下来开始攻打非线性 SVM!
3. 非线性支持向量机
上面讲了线性可分和近似线性可分情况下的 SVM,现在来看最后一种例子——完全线性不可分的情况。
要说非线性,最经典的肯定是这个 “异或” 图:我们无法找到一条直线来分开两组点。
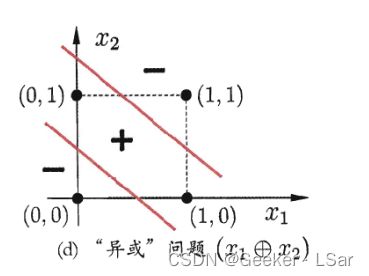
上一篇讲过,所谓线性不可分就是无法用一个超平面把两组/多组数据分隔开。
不过,好就好在,“非(停顿)线性可分” 同时意味着 “非线性(停顿)可分”(怎么感觉我在抖机灵(((),也就是说,虽然找不到线性分类面分开这些数据,但是能找到非线性分类面,也就是曲面或者超曲面来分开这些数据,所以这种问题是可解的,不过会麻烦点。
同时,对于线性不可分的数据,可以对它们进行非线性变换,变成线性可分的数据。
大概就是:线性不可分数据 + 非线性变换 ——> 线性可分数据。(其实 “非线性变换” 应该写在反应条件而不是反应物((
非线性变换通常是将低维空间中线性不可分的数据映射到高维空间中,使其变为在高维空间中线性可分的数据。也就是将原本用较少的特征来描述代表的数据,转换为用较多的特征来描述的数据。
用于非线性变换(高维映射)的函数被称为核函数。
其实核函数本身和映射并没有直接联系,但是它提供了在高维空间中计算内积的简便方法。换言之,如果不利用核函数,在高维空间中计算内积简直就是一种灾难,但是核函数技术可以避免这种 “维度灾难”。
关于低维线性不可分数据集映射到高维后变得线性可分这件事,举两个例子。
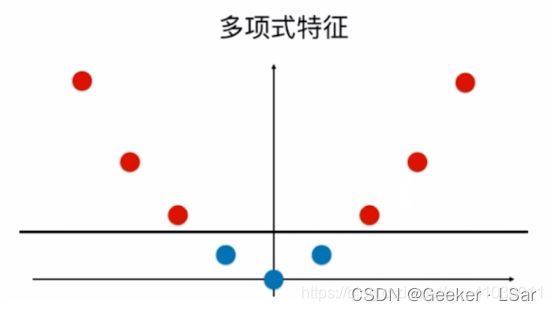
先来看一个特别形象的,一条直线(一维空间)上有蓝色和红色的点,这肯定是线性不可分的。

然而,当我们把这些点 “映射” 到高维空间,比如二维平面,让 y y y 轴的坐标为 x 2 x^2 x2:
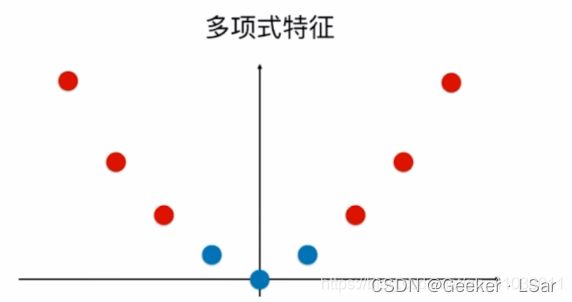
核函数本质上也在做同样的事。
再举一个严谨一点的例子,以下图为例:
用数学语言表示,设左边原空间为( R 2 R^2 R2 表示平面点集): x ⊂ R 2 , z = ( x ( 1 ) , x ( 2 ) ) T ⊂ x x\subset R^2, z = (x^{(1)}, x^{(2)})^T \subset x x⊂R2,z=(x(1),x(2))T⊂x右边新空间为: z ⊂ R 2 , z = ( z ( 1 ) , z ( 2 ) ) T ⊂ x z\subset R^2, z = (z^{(1)}, z^{(2)})^T \subset x z⊂R2,z=(z(1),z(2))T⊂x
则原空间到新空间的映射为: z = φ ( x ) = ( ( x ( 1 ) ) 2 , ( x ( 2 ) ) 2 ) T z = φ(x) = ((x^{(1)})^2, (x^{(2)})^2)^T z=φ(x)=((x(1))2,(x(2))2)T
这样,原空间 X ⊂ R 2 X\subset R^2 X⊂R2 变成了新空间 Z ⊂ R 2 Z\subset R^2 Z⊂R2,原空间中的椭圆(超曲面)也相应变成了新空间中的直线(超平面)。
在变换后的新空间里,可以用一个超平面将正负样本分开了,原问题也就转化成为高维空间中的线性可分问题。
也就是说,用线性分类方法求解非线性可分问题分为两步:
- 使用非线性变换将原空间映射到新空间(高维)
- 在新的高维空间中利用线性可分 SVM 求解
核技巧就属于这样的方法。
常用的核函数有:线性核函数、多项式核函数、高斯核函数等。 以下是它们的表示:
线性核函数:这是核函数中最简单的一种。 k ( x , z ) = x ⋅ z + c k(x, z) = x · z+c k(x,z)=x⋅z+c
多项式核函数:其中 a 、 c 、 p a、c、p a、c、p 都是实系数,线性核函数是多项式核函数的一个特例。 k ( x , z ) = ( a x ⋅ z + c ) p k(x, z) = (ax · z+c)^p k(x,z)=(ax⋅z+c)p
高斯核函数/径向基函数(RBF):高斯核函数可将输入空间映射到无穷维的特征空间中。 K ( x i , x j ) = e x p − γ ∣ ∣ x i − x j ∣ ∣ 2 K(xi, xj) = exp^{-γ||xi-xj||^2} K(xi,xj)=exp−γ∣∣xi−xj∣∣2
核函数还有很多,不一一举例啦,它们的原理大体上都是相似的。
不过,在什么场景使用什么核函数并不是一件确定的事,and 核函数调参数也并不简单)))从理解到用好还是有很长的路要走的。
ok!!!!!以上就是关于支持向量机的详细讲解!!一万字啦!
嘿嘿真的非常开心你能够看到这里!!一起加油!
如果有任何 bug 欢迎评论区拷打我!!
这篇文章写了两天,准确来说是【一个晚上 3000 字】+【一个半天 7000 字】,查了无数篇资料,每一个词每一句话都反复斟酌了很久,希望对你有所帮助!⭐
——Geeker_LStar