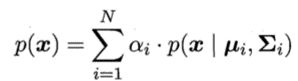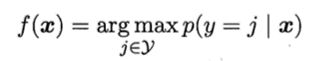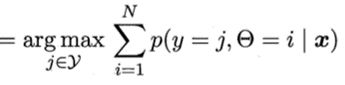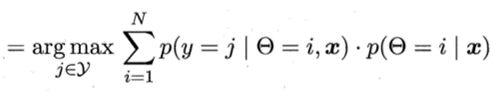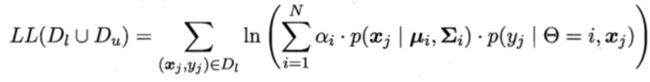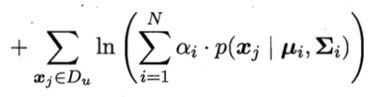机器学习---半监督学习（生成式方法）

1. 主动学习

形式化地看，我们有训练样本集，这l个样本的类别标记（即是否

好瓜）已知，称为“有标记”(labeled)样本；此外，还有，这u

个样本的类别标记未知（即不知是否好瓜)，称为“未标记”(unlabeled)样本。若直接使用传统监督学

习技术，则仅有Dl能用于构建模型，Du所包含的信息被浪费了；另一方面，若Dl较小，则由于训

练样本不足，学得模型的泛化能力往往不佳。那么，能否在构建模型的过程中将Du利用起来呢？

一个简单的做法，是将Du中的示例全部标记后用于学习。这就相当于请瓜农把地里的瓜全都检查

一遍，告诉我们哪些是好瓜，哪些不是好瓜，然后再用于模型训练。显然，这样做需耗费瓜农大量

时间和精力。有没有“便宜”一点的办法呢？

我们可以用Dl先训练一个模型，拿这个模型去地里挑一个瓜，询问瓜农好不好，然后把这个新获得

的有标记样本加入Dl中重新训练一个模型，再去挑瓜，… 这样，若每次都挑出对改善模型性能帮

助大的瓜，则只需询问瓜农比较少的瓜就能构建出比较强的模型，从而大幅降低标记成本。这样的

学习方式称为“主动学习”(active learning)，其目标是使用尽量少的“查询”(query)来获得尽量好的性

能。若不引入专家知识，还能利用未标记昂本提高分类器泛化性能吗？

2. 半监督学习

事实上，未标记样本虽未直接包含标记信息，但若它们与有标记样本是从同样的数据源独立同分布

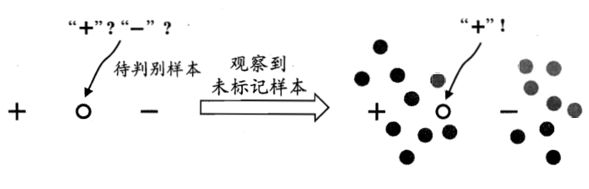
采样而来，则它们所包含的关于数据分布的信息对建立模型将大有裨益。图1给出了一个直观的

例示。若仅基于图中的一个正例和一个反例，则由于待判别样本恰位于两者正中间，大体上只能随

机猜测；若能观察到图中的未标记样本，则将很有把握地判别为正例。

让学习器不依赖外界交互、自动地利用未标记样本来提升学习性能，就是半监督学习(semi-

supervised learning)。

半监督学习的现实需求非常强烈，因为在现实应用中往往能容易地收集到大量未标记样本，而获取

“标记”却需耗费人力、物力。例如，在进行计算机辅助医学影像分析时，可以从医院获得大量医学

影像，但若希望医学专家把影像中的病灶全都标识出来则是不现实的。“有标记数据少，未标记数

据多”这个现象在互联网应用中更明显，例如在进行网页推荐时需请用户标记出感兴趣的网页，但

很少有用户愿花很多时间来提供标记，因此，有标记网页样本少，但互联网上存在无数网页可作为

未标记样本来使用。半监督学习恰是提供了一条利用“廉价”的未标记样本的途径。

要利用未标记样本，必然要做一些将未标记样本所揭示的数据分布信息与类别标记相联系的假设。

最常见的是“聚类假设”(cluster assumption)，即假设数据存在簇结构，同一个簇的样本属于同一个

类别。图1就是基于聚类假设来利用未标记样本，由于待预测样本与正例样本通过未标记样本的

“撮合”聚在一起，与相对分离的反例样本相比，待判别样本更可能属于正类。半监督学习中另一种

常见的假设是“流形假设”(manifold assumption)，即假设数据分布在一个流形结构上，邻近的样本

拥有相似的输出值。“邻近”程度常用“相似”程度来刻画，因此，流形假设可看作聚类假设的推广，

但流形假设对输出值没有限制，因此比聚类假设的适用范围更广，可用于更多类型的学习任务。事

实上，无论聚类假设还是流形假设，其本质都是“相似的样本拥有相似的输出”，这个基本假设。

半监督学习可进一步划分为纯(pure)半监督学习和直推学习(transductivelearning)，前者假定训练

数据中的未标记样本并非待预测的数据，而后者则假定学习过程中所考虑的未标记样本恰是待预测

数据，学习的目的就是在这些未标记样本上获得最优泛化性能。换言之，纯半监督学习是基于“开

放世界”假设，希望学习模型能适用于训练过程中未观察到的数据；而直推学习是基于“封闭世界”假

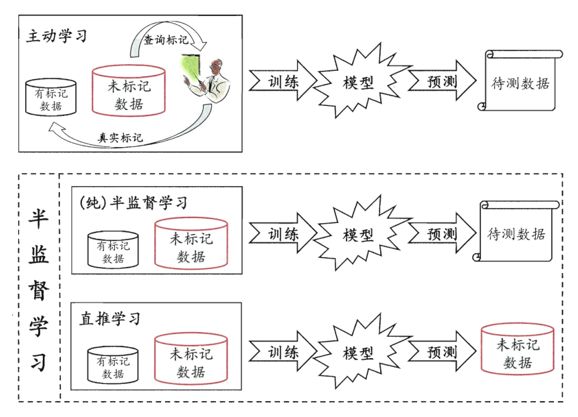
设，仅试图对学习过程中观察到的未标记数据进行预测。图2直观地显示出主动学习、纯半监督

学习、直推学习的区别。需注意的是，纯半监督学习和直推学习常合称为半监督学习。

3. 生成式方法 

生成式方法(generative methods)是直接基于生成式模型的方法。此类方法假设所有数据（无论是

否有标记）都是由同一个潜在的模型“生成”的。这个假设使得我们能通过潜在模型的参数将未标记

数据与学习目标联系起来，而未标记数据的标记则可看作模型的缺失参数，通常可基于EM算法进

行极大似然估计求解。此类方法的区别主要在于生成式模型的假设，不同的模型假设将产生不同的

方法。

给定样本x，其真实类别标记为y∈Y，其中Y∈{1,2,..,N}为所有可能的类别。假设样本由高斯混合

模型生成，且每个类别对应一个高斯混合成分。换言之，数据样本是基于如下概率密度生成：

其中，混合系数是样本x属于第i个高

斯混合成分的概率；μi和∑i为该高斯混合成分的参数。

令f(x)∈y表示模型f对x的预测标记，Θ∈{1,2，...，N}表示样本x隶属的高斯混合成分。由最大化后

验概率可知

其中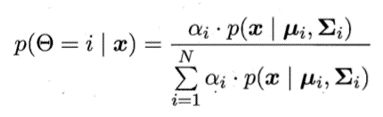：为样本x由第i个高斯混合成分生成的后验概率，p(y=j|Θ=i,x)

为x由第i个高斯混合成分生成且其类别为的概率。由于假设每个类别对应一个高斯混合成分，因此

p(y=j|Θ=i,x)仅与样本x所属的高斯混合成分日有关，可用p(y=j|Θ=i)代替。不失一般性，假定第i个

类别对应于第i个高斯混合成分，即p(y=j|Θ=i)=1当且仅当i=j，否则p(y=j|Θ=i)=0。

不难发现，上式中估计p(y=j|Θ=i,x)需知道样本的标记，因此仅能使用有标记数据；而p(Θ=i|x)不涉

及样本标记，因此有标记和未标记数据均可利用，通过引入大量的未标记数据，对这一项的估计可

望由于数据量的增长而更为准确，于是上式整体的估计可能会更准确.由此可清楚地看出未标记数

据何以能辅助提高分类模型的性能。

给定有标记样本集和未标记样本集

。假设所有样本独立同分布，且都是由同

一个高斯混合模型生成的。用极大似然法来估计高斯混合模型的参数

的对数似然是由两项

组成：基于有标记数据Dl的有监督项和基于未标记数据Du的无监督项。显然，高斯混合模型参数

估计可用EM算法求解，迭代更新式如下：

E步：根据当前模型参数计算未标记样本x属于各高斯混合成分的概率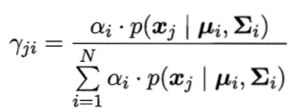

M步：基于Y更新模型参数，其中：表示第i类的有标记样本数目

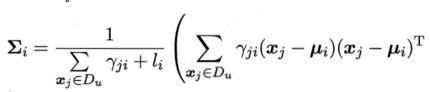
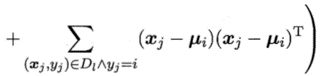
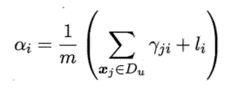以上过程不断迭代直至收敛，即可获得模型参数。然后由前面的式子f(x)和

p(Θ=i|x)就能对样本进行分类。

将上述过程中的高斯混合模型换成混合专家模型[Miller and Uyar,1997]、朴素贝叶斯模型[Nigam et

al.,2000]等即可推导出其他的生成式半监督学习方法。此类方法简单，易于实现，在有标记数据极

少的情形下往往比其他方法性能更好。然而，此类方法有一个关键：模型假设必须准确，即假设的

生成式模型必须与真实数据分布吻合；否则利用未标记数据反倒会降低泛化性能[Cozman and

Cohen,2002]。遗憾的是，在现实任务中往往很难事先做出准确的模型假设，除非拥有充分可靠的

领域知识。