双非本科准备秋招（13.1）—— 力扣 栈、队列与堆

1、103. 二叉树的锯齿形层序遍历

昨天做的二叉树的层序遍历，把代码直接拿过来。

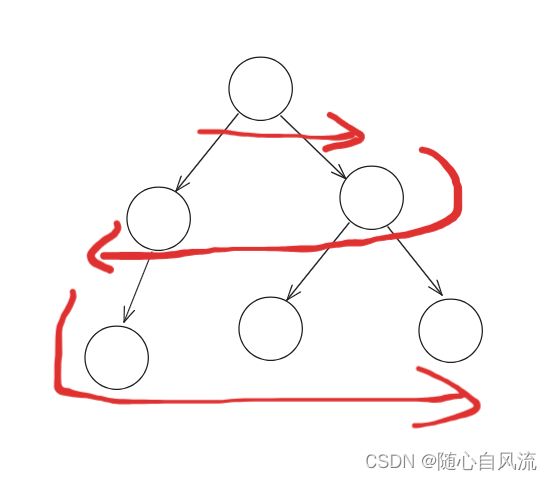
这个题要求的是一个Z型遍历，如下图。

        用一个变量f记录正反顺序，然后使用LinkedList记录答案，下图可以看到LinkedList继承了Deque，所以可以当作双端队列来用。

每次记录答案时，根据f的值选择调用offerLast和offerFirst方法。

class Solution {
    public List> zigzagLevelOrder(TreeNode root) {
        LinkedBlockingQueue q = new LinkedBlockingQueue<>();
        List> list = new ArrayList<>();
        if(root == null) return list;
        q.offer(root);
        int cnt = 1;
        boolean f = true;

        while(!q.isEmpty()){
            LinkedList L = new LinkedList<>();
            int temp = 0;
            for(int i = 0; i < cnt; i++){
                TreeNode t = q.poll();
                if(f) L.offerLast(t.val);
                else L.offerFirst(t.val);
                if(t.left != null){
                    q.offer(t.left);
                    temp++;
                }
                if(t.right != null){
                    q.offer(t.right);
                    temp++;
                }
            }
            cnt = temp;
            list.add(L);
            f = !f;
        }

        return list;
    }
}

2、23. 合并 K 个升序链表

        用优先队列来做，默认排序即可（小顶堆），最后处理一下答案，把队列q中的元素转移到新的链表上。

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        PriorityQueue q = new PriorityQueue<>();
        ListNode head = new ListNode();
        ListNode p = head;
        for(int i = 0; i < lists.length; i++){
            while(lists[i] != null){
                q.offer(lists[i].val);
                lists[i] = lists[i].next;
            }
        }
        while(!q.isEmpty()){
            ListNode t = new ListNode(q.poll());
            p.next = t;
            p = p.next;
        }
        return head.next;
    }
}

3、215. 数组中的第K个最大元素

堆这种数据结构就适合求前几个具有xx特性的元素问题，包括下一个题目和最后一个题目。

这个题用小顶堆做，我们可以手写一个堆的结构class MinHeap。

我们只需要把前k个元素加入堆（offer()方法），然后后面的元素只需要判断是否大于堆中的第一个元素即可，如果大于，就替换第一个元素（replace()方法）。

因为堆中第一个元素是k个中最小的，我们不断加入大的元素，那么最后是不是堆中只剩下最大的k个元素了，k个最大元素中最小的不就是堆的第一个元素嘛。

class Solution {
    public int findKthLargest(int[] nums, int k) {
        MinHeap heap = new MinHeap(k);

        for(int i = 0; i < k; i++){
            heap.offer(nums[i]);
        }

        for(int i = k; i < nums.length; i++){
            if(nums[i] > heap.array[0]){
                heap.replace(nums[i]);
            }
        }

        return heap.array[0];
    }
}

public class MinHeap {
    int[] array;
    int size;

    public MinHeap(int capacity) {
        this.array = new int[capacity];
    }

    public void offer(int offerd){
        up(offerd);
        size++;   
    }

    public void up(int offerd){
        int child = size;
        while(child > 0){
            int parent = (child-1)/2;
            if(array[parent] > offerd){
                array[child] = array[parent];
            }
            else{
                break;
            }
            child = parent;
        }
        array[child] = offerd;
    }

    public void replace(int replaced){
        array[0] = replaced;
        down(0);
    }

    private void down(int parent) {
        int lc = parent*2+1;
        int rc = lc+1;
        int min = parent;
        if(lc < size && array[lc] < array[min]){
            min = lc;
        }
        if(rc < size && array[rc] < array[min]){
            min = rc;
        }
        if(min != parent){
            swap(min, parent);
            down(min);
        }
    }

    private void swap(int i, int j) {
        int t = array[i];
        array[i] = array[j];
        array[j] = t;
    }
}

4、703. 数据流中的第 K 大元素

与上个题不能说一模一样，只能说完全一致。

需要注意add方法要判断一下堆是不是满了，因为初始化堆的时候有可能提供的元素个数小于k个，如果没满直接加入堆就好。

class KthLargest {
    MinHeap heap = null;
    public KthLargest(int k, int[] nums) {
        heap = new MinHeap(k);
        int len = Math.min(k, nums.length);
        for(int i = 0; i < len; i++){
            heap.offer(nums[i]);
        }
        for(int i = k; i < nums.length; i++){
            if(nums[i] > heap.array[0]){
                heap.replace(nums[i]);
            }
        }
    }
    
    public int add(int val) {
        if(heap.size < heap.array.length){
            heap.offer(val);
        }
        else if(val > heap.array[0]){
            heap.replace(val);
        }
        return heap.array[0];
    }
}

public class MinHeap {
    int[] array;
    int size;

    public MinHeap(int capacity) {
        this.array = new int[capacity];
        Arrays.fill(this.array, Integer.MIN_VALUE);
    }

    public void offer(int offerd){
        up(offerd);
        size++;   
    }

    public void up(int offerd){
        int child = size;
        while(child > 0){
            int parent = (child-1)/2;
            if(array[parent] > offerd){
                array[child] = array[parent];
            }
            else{
                break;
            }
            child = parent;
        }
        array[child] = offerd;
    }

    public void replace(int replaced){
        array[0] = replaced;
        down(0);
    }

    private void down(int parent) {
        int lc = parent*2+1;
        int rc = lc+1;
        int min = parent;
        if(lc < size && array[lc] < array[min]){
            min = lc;
        }
        if(rc < size && array[rc] < array[min]){
            min = rc;
        }
        if(min != parent){
            swap(min, parent);
            down(min);
        }
    }

    private void swap(int i, int j) {
        int t = array[i];
        array[i] = array[j];
        array[j] = t;
    }
}

5、1047. 删除字符串中的所有相邻重复项

解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

读完解释后，感觉就是明示了栈的数据结构。

我们把a入栈，b入栈，b入栈，b和栈顶重复，b不入了并且弹出栈顶元素，这时候栈只剩下a，然后a入栈，a和栈顶重复，a不入了并且弹出栈顶元素，栈空了，然后c入栈，a入栈。

这时候我们依次弹出，得到ac，那么我们可以倒着遍历字符串，倒着入栈，结果都是一样的，不影响删除相邻重复的字母。

class Solution {
    public String removeDuplicates(String s) {
        Stack stack = new Stack<>();
        for(int i = s.length()-1; i >= 0; i--){
            if(!stack.isEmpty() && stack.peek() == s.charAt(i)){
                stack.pop();
            }
            else{
                stack.push(s.charAt(i));
            }
        }
        String ans = "";
        while(!stack.isEmpty()){
            ans += stack.pop();
        }

        return ans;
    }
}

6、347. 前 K 个高频元素

        元素与元素的次数，让人联想到哈希表。存到哈希表后，对出现的次数进行排序，这应该是第一思路。

        前k个高频元素，有出现了前几个具有xx特性的这种要求，我们就会想到堆，在堆中只存放前k个高频元素，使用小顶堆，我们最后得到的就是前k个最高频的元素了。

        java中的ProrityQueue的底层就是堆，我就不用自己写的了。因为我们的堆中要存储数据和出现的次数，因此可以存个数组，下标0代表是什么数据，下标1代表出现的次数。        

        我们先加入到map中，然后遍历map集合，把cnt大于堆顶的元素替换掉原来的元素，也就是队列出队，这样就得到了前k个高频的元素了。

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        PriorityQueue q = new PriorityQueue<>(k, (o1, o2) -> o1[1] - o2[1]);
        HashMap map = new HashMap<>();

        for(int i = 0; i < nums.length; i++){
            int v = 0;
            if(map.containsKey(nums[i])){
                v = map.get(nums[i]);
            }
            map.put(nums[i], v+1);
        }

        for(Integer n : map.keySet()){
            int cnt = map.get(n);
            if(q.size() < k){
                q.offer(new int[]{n, cnt});
            }
            else if(cnt > q.peek()[1]){
                q.poll();
                q.offer(new int[]{n, cnt});
            }
        }

        int[] ans = new int[k];
        int j = 0;
        while(!q.isEmpty()){
            ans[j++] = q.poll()[0];
        }
        return ans;
    }
}