每日一题合集1

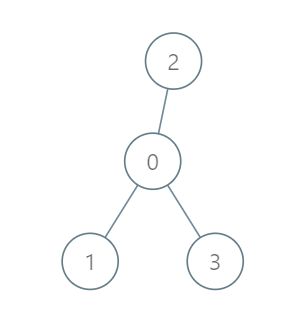
1038 从二叉搜索树到更大和树

1038. 从二叉搜索树到更大和树 - 力扣（LeetCode）

二叉树的中序遍历+逆向思维

给定一个二叉搜索树 root (BST)，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

提醒一下， 二叉搜索树 满足下列约束条件：

• 节点的左子树仅包含键 小于 节点键的节点。
• 节点的右子树仅包含键 大于 节点键的节点。
• 左右子树也必须是二叉搜索树。

示例 1：

输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

提示：

• 树中的节点数在 [1, 100] 范围内。
• 0 <= Node.val <= 100
• 树中的所有值均 不重复 。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int cur;

    public TreeNode bstToGst(TreeNode root) {
        dfs(root);
        return root;
    }

    public void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        dfs(root.right);
        cur += root.val;
        root.val = cur;
        dfs(root.left);
    }
}

2477 到达首都的最少油耗

2477. 到达首都的最少油耗 - 力扣（LeetCode）

图论 树形DP

向上取整 (x+y-1)/y

给你一棵 n 个节点的树（一个无向、连通、无环图），每个节点表示一个城市，编号从 0 到 n - 1 ，且恰好有 n - 1 条路。0 是首都。给你一个二维整数数组 roads ，其中 roads[i] = [ai, bi] ，表示城市 ai 和 bi 之间有一条 双向路 。

每个城市里有一个代表，他们都要去首都参加一个会议。

每座城市里有一辆车。给你一个整数 seats 表示每辆车里面座位的数目。

城市里的代表可以选择乘坐所在城市的车，或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。

请你返回到达首都最少需要多少升汽油。

示例 1：

输入：roads = [[0,1],[0,2],[0,3]], seats = 5
输出：3
解释：
- 代表 1 直接到达首都，消耗 1 升汽油。
- 代表 2 直接到达首都，消耗 1 升汽油。
- 代表 3 直接到达首都，消耗 1 升汽油。
最少消耗 3 升汽油。

示例 2：

输入：roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
输出：7
解释：
- 代表 2 到达城市 3 ，消耗 1 升汽油。
- 代表 2 和代表 3 一起到达城市 1 ，消耗 1 升汽油。
- 代表 2 和代表 3 一起到达首都，消耗 1 升汽油。
- 代表 1 直接到达首都，消耗 1 升汽油。
- 代表 5 直接到达首都，消耗 1 升汽油。
- 代表 6 到达城市 4 ，消耗 1 升汽油。
- 代表 4 和代表 6 一起到达首都，消耗 1 升汽油。
最少消耗 7 升汽油。

示例 3：

输入：roads = [], seats = 1
输出：0
解释：没有代表需要从别的城市到达首都。

提示：

• 1 <= n <= 105
• roads.length == n - 1
• roads[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• roads 表示一棵合法的树。
• 1 <= seats <= 105

class Solution {
    private long ans;

    public long minimumFuelCost(int[][] roads, int seats) {
        int n = roads.length;
        List<Integer>[] g = new ArrayList[n + 1];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (var r : roads) {
            int x = r[0], y = r[1];
            g[x].add(y);
            g[y].add(x);
        }
        dfs(0, -1, g, seats);
        return ans;
    }

    private int dfs(int x, int father, List<Integer>[] g, int seats) {
        int size = 1;
        for (int y : g[x]) {
            if (y != father) {
                size += dfs(y, x, g, seats);
            }
        }
        if (x > 0) {
            // ans += (size - 1) / seats + 1;//向上取整(size/seats)
            ans += Math.ceil(1.0 * size / seats);
        }
        return size;
    }
}

2646 最小化旅行的价值总和

2646. 最小化旅行的价格总和 - 力扣（LeetCode）

图论 树形DP 经典题

现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

示例 1：

输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。

示例 2：

输入：n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出：1
解释：
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 并使其价格减半后的树。 
第 1 次旅行，选择路径 [0] 。路径的价格总和为 1 。 
所有旅行的价格总和为 1 。可以证明，1 是可以实现的最小答案。

提示：

• 1 <= n <= 50
• edges.length == n - 1
• 0 <= ai, bi <= n - 1
• edges 表示一棵有效的树
• price.length == n
• price[i] 是一个偶数
• 1 <= price[i] <= 1000
• 1 <= trips.length <= 100
• 0 <= starti, endi <= n - 1

class Solution {
    private List<Integer>[] g;
    private int[] price, cnt;
    private int end;

    public int minimumTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {
        g = new ArrayList[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        for (var e : edges) {
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x);
        }
        this.price = price;
        cnt = new int[n];
        for (var t : trips) {
            end = t[1];
            path(t[0], -1);
        }
        int[] p = dfs(0, -1);
        return Math.min(p[0], p[1]);
    }

    //求经过点的次数
    private boolean path(int x, int father) {
        if (x == end) {
            cnt[x]++;
            return true;
        }
        for (int y : g[x]) {
            if (y != father && path(y, x)) {
                cnt[x]++;
                return true;
            }
        }
        return false;
    }

    //求价值总和 选/不选
    private int[] dfs(int x, int father) {
        int notselect = price[x] * cnt[x];
        int select = notselect / 2;
        for (int y : g[x]) {
            if (y != father) {
                int[] p = dfs(y, x);
                notselect += Math.min(p[0], p[1]);
                select += p[0];
            }
        }
        return new int[]{notselect, select};
    }
}

1466 重新规划路线

1466. 重新规划路线 - 力扣（LeetCode）

图论 树形DP DFS

n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。

今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。

题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。

示例 1：

输入：n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出：3
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 2：

输入：n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
输出：2
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 3：

输入：n = 3, connections = [[1,0],[2,0]]
输出：0

提示：

• 2 <= n <= 5 * 10^4
• connections.length == n-1
• connections[i].length == 2
• 0 <= connections[i][0], connections[i][1] <= n-1
• connections[i][0] != connections[i][1]

class Solution {
    public int minReorder(int n, int[][] connections) {
        List<int[]>[] g = new List[n];
        Arrays.setAll(g, e -> new ArrayList<int[]>());
        for (var c : connections) {
            int x = c[0], y = c[1];
            g[x].add(new int[]{y, 1});
            g[y].add(new int[]{x, 0});
        }
        return dfs(0, -1, g);
    }

    public int dfs(int x, int fa, List<int[]>[] g) {
        int ans = 0;
        for (var y : g[x]) {
            if (y[0] != fa) {
                ans += y[1] + dfs(y[0], x, g);
            }
        }
        return ans;
    }
}

2008 出租车的最大盈利

2008. 出租车的最大盈利 - 力扣（LeetCode）

动态规划 记忆化搜索 递推

你驾驶出租车行驶在一条有 n 个地点的路上。这 n 个地点从近到远编号为 1 到 n ，你想要从 1 开到 n ，通过接乘客订单盈利。你只能沿着编号递增的方向前进，不能改变方向。

乘客信息用一个下标从 0 开始的二维数组 rides 表示，其中 rides[i] = [starti, endi, tipi] 表示第 i 位乘客需要从地点 starti 前往 endi ，愿意支付 tipi 元的小费。

每一位 你选择接单的乘客 i ，你可以 盈利 endi - starti + tipi 元。你同时 最多 只能接一个订单。

给你 n 和 rides ，请你返回在最优接单方案下，你能盈利 最多 多少元。

**注意：**你可以在一个地点放下一位乘客，并在同一个地点接上另一位乘客。

示例 1：

输入：n = 5, rides = [[2,5,4],[1,5,1]]
输出：7
解释：我们可以接乘客 0 的订单，获得 5 - 2 + 4 = 7 元。

示例 2：

输入：n = 20, rides = [[1,6,1],[3,10,2],[10,12,3],[11,12,2],[12,15,2],[13,18,1]]
输出：20
解释：我们可以接以下乘客的订单：
- 将乘客 1 从地点 3 送往地点 10 ，获得 10 - 3 + 2 = 9 元。
- 将乘客 2 从地点 10 送往地点 12 ，获得 12 - 10 + 3 = 5 元。
- 将乘客 5 从地点 13 送往地点 18 ，获得 18 - 13 + 1 = 6 元。
我们总共获得 9 + 5 + 6 = 20 元。

提示：

• 1 <= n <= 105
• 1 <= rides.length <= 3 * 104
• rides[i].length == 3
• 1 <= starti < endi <= n
• 1 <= tipi <= 105

class Solution {
    public long maxTaxiEarnings(int n, int[][] rides) {
        List<int[]>[] groups = new ArrayList[n + 1];
        for (var r : rides) {
            int start = r[0], end = r[1], tip = r[2];
            if (groups[end] == null) {
                groups[end] = new ArrayList<>();
            }
            groups[end].add(new int[]{start, end - start + tip});
        }
        long[] cache = new long[n + 1];
        Arrays.fill(cache, -1);
        return dfs(n, groups, cache);
    }

    public long dfs(int i, List<int[]>[] groups, long[] cache) {
        if (i == 1) {
            return 0;
        }
        if (cache[i] != -1) {
            return cache[i];
        }
        long res = dfs(i - 1, groups, cache);
        if (groups[i] != null) {
            for (var p : groups[i]) {
                res = Math.max(res, dfs(p[0], groups, cache) + p[1]);
            }
        }
        return cache[i] = res;
    }
}

class Solution {
    public long maxTaxiEarnings(int n, int[][] rides) {
        List<int[]>[] groups = new ArrayList[n + 1];
        for (var r : rides) {
            int start = r[0], end = r[1], tip = r[2];
            if (groups[end] == null) {
                groups[end] = new ArrayList<>();
            }
            groups[end].add(new int[]{start, end - start + tip});
        }
        long[] f = new long[n + 1];
        for (int i = 2; i <= n; i++) {
            f[i] = f[i - 1];
            if (groups[i] != null) {
                for (var p : groups[i]) {
                    f[i] = Math.max(f[i], f[p[0]] + p[1]);
                }
            }
        }
        return f[n];
    }
}

附加题

2830. 销售利润最大化 - 力扣（LeetCode）

1235. 规划兼职工作 - 力扣（LeetCode）

1751. 最多可以参加的会议数目 II - 力扣（LeetCode）

2048 下一个更大的数值平均数

2048. 下一个更大的数值平衡数 - 力扣（LeetCode）

暴力枚举 打表 二分查找

如果整数 x 满足：对于每个数位 d ，这个数位 恰好 在 x 中出现 d 次。那么整数 x 就是一个 数值平衡数 。

给你一个整数 n ，请你返回 严格大于 n 的 最小数值平衡数 。

示例 1：

输入：n = 1
输出：22
解释：
22 是一个数值平衡数，因为：
- 数字 2 出现 2 次 
这也是严格大于 1 的最小数值平衡数。

示例 2：

输入：n = 1000
输出：1333
解释：
1333 是一个数值平衡数，因为：
- 数字 1 出现 1 次。
- 数字 3 出现 3 次。 
这也是严格大于 1000 的最小数值平衡数。
注意，1022 不能作为本输入的答案，因为数字 0 的出现次数超过了 0 。

示例 3：

输入：n = 3000
输出：3133
解释：
3133 是一个数值平衡数，因为：
- 数字 1 出现 1 次。
- 数字 3 出现 3 次。 
这也是严格大于 3000 的最小数值平衡数。

提示：

• 0 <= n <= 106

class Solution {
    public int nextBeautifulNumber(int n) {
        for (int i = n + 1; i <= 1224444; i++) {
            if (isBalance(i)) {
                return i;
            }
        }
        return -1;
    }

    public boolean isBalance(int x) {
        int[] cnt = new int[10];
        while (x > 0) {
            cnt[x % 10]++;
            x /= 10;
        }
        for (int i = 0; i < 10; i++) {
            if (cnt[i] > 0 && cnt[i] != i) {
                return false;
            }
        }
        return true;
    }
}

70 爬楼梯

70. 爬楼梯 - 力扣（LeetCode）

动态规划DP

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

• 1 <= n <= 45

class Solution {
    public int climbStairs(int n) {
        // int[] dp = new int[n + 2];
        // dp[0] = 1;
        // dp[1] = 1;
        // for (int i = 2; i <= n; i++) {
        //     dp[i] = dp[i - 1] + dp[i - 2];
        // } 
        // return dp[n];
        //找到规律不难发现为斐波那契数列
        int sum, a = 1, b = 1;
        for (int i = 2; i <= n; i++) {
            sum = a + b;
            a = b;
            b = sum;
        }
        return b;
    }
}

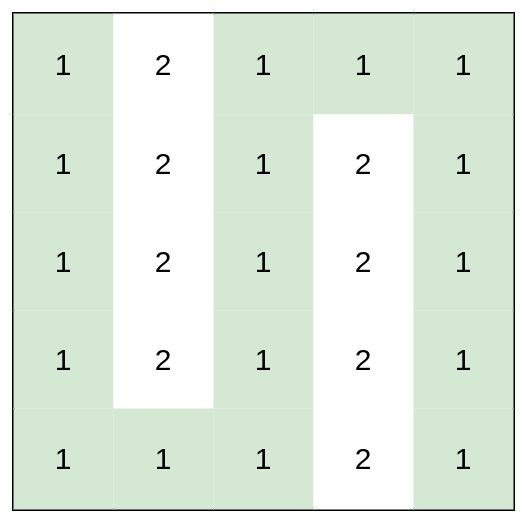
1631 最小体力消耗路径

1631. 最小体力消耗路径 - 力扣（LeetCode）

二分查找 并查集 图论 最短路径Dijkstra算法

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

示例 1：

输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 106

class Solution {
    public int minimumEffortPath(int[][] heights) {
        int m = heights.length, n = heights[0].length;
        UnionFind uf = new UnionFind(m * n);
        List<int[]> edges = new ArrayList<>();
        int[] dirs = new int[]{1, 0, 1};
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                for (int k = 0; k < 2; k++) {
                    int x = i + dirs[k], y = j + dirs[k + 1];
                    if (x >= 0 && x < m && y >= 0 && y < n) {
                        int d = Math.abs(heights[i][j] - heights[x][y]);
                        edges.add(new int[]{d, i * n + j, x * n + y});
                    }
                }
            }
        }
        Collections.sort(edges, (a, b) -> a[0] - b[0]);
        for (var e : edges) {
            uf.union(e[1], e[2]);
            if (uf.connected(0, m * n - 1)) {
                return e[0];
            }
        }
        return 0;
    }
}

class UnionFind {
    private final int[] p;
    private final int[] size;

    public UnionFind(int n) {
        p = new int[n];
        size = new int[n];
        for (int i = 0; i < n; i++) {
            p[i] = i;
            size[i] = i;
        }
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    public boolean union(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa == pb) {
            return false;
        }
        if (size[pa] > size[pb]) {
            p[pb] = pa;
            size[pa] += size[pb];
        } else {
            p[pa] = pb;
            size[pb] += size[pa];
        }
        return true;
    }

    public boolean connected(int a, int b) {
        return find(a) == find(b);
    }
}

2454 下一个更大元素Ⅳ

2454. 下一个更大元素 IV - 力扣（LeetCode）

单调栈

给你一个下标从 0 开始的非负整数数组 nums 。对于 nums 中每一个整数，你必须找到对应元素的 第二大 整数。

如果 nums[j] 满足以下条件，那么我们称它为 nums[i] 的 第二大 整数：

• j > i
• nums[j] > nums[i]
• 恰好存在 一个 k 满足 i < k < j 且 nums[k] > nums[i] 。

如果不存在 nums[j] ，那么第二大整数为 -1 。

• 比方说，数组 [1, 2, 4, 3] 中，1 的第二大整数是 4 ，2 的第二大整数是 3 ，3 和 4 的第二大整数是 -1 。

请你返回一个整数数组 answer ，其中 answer[i]是 nums[i] 的第二大整数。

示例 1：

输入：nums = [2,4,0,9,6]
输出：[9,6,6,-1,-1]
解释：
下标为 0 处：2 的右边，4 是大于 2 的第一个整数，9 是第二个大于 2 的整数。
下标为 1 处：4 的右边，9 是大于 4 的第一个整数，6 是第二个大于 4 的整数。
下标为 2 处：0 的右边，9 是大于 0 的第一个整数，6 是第二个大于 0 的整数。
下标为 3 处：右边不存在大于 9 的整数，所以第二大整数为 -1 。
下标为 4 处：右边不存在大于 6 的整数，所以第二大整数为 -1 。
所以我们返回 [9,6,6,-1,-1] 。

示例 2：

输入：nums = [3,3]
输出：[-1,-1]
解释：
由于每个数右边都没有更大的数，所以我们返回 [-1,-1] 。

提示：

• 1 <= nums.length <= 105
• 0 <= nums[i] <= 109

class Solution {
    private int MX = 100000;
    private int[] s = new int[MX];
    private int[] t = new int[MX];

    public int[] secondGreaterElement(int[] nums) {
        int n = nums.length;
        int lenS = 0, lenT = 0;
        int[] ans = new int[n];
        Arrays.fill(ans, -1);
        for (int i = 0; i < n; i++) {
            int num = nums[i];
            while (lenT > 0 && nums[t[lenT - 1]] < num) {
                ans[t[--lenT]] = num;//t栈顶的第二个更大元素是x
            }
            int temp = lenS;
            while (lenS > 0 && nums[s[lenS - 1]] < num) {
                lenS--;//s栈顶的第一个更大元素是x
            }
            System.arraycopy(s, lenS, t, lenT, temp - lenS);
            lenT += temp - lenS;
            s[lenS++] = i;
        }
        return ans;
    }
}

2697 字典序最小回文串

2697. 字典序最小回文串 - 力扣（LeetCode）

贪心 双指针

给你一个由 小写英文字母 组成的字符串 s ，你可以对其执行一些操作。在一步操作中，你可以用其他小写英文字母 替换 s 中的一个字符。

请你执行 尽可能少的操作 ，使 s 变成一个 回文串 。如果执行 最少 操作次数的方案不止一种，则只需选取 字典序最小 的方案。

对于两个长度相同的字符串 a 和 b ，在 a 和 b 出现不同的第一个位置，如果该位置上 a 中对应字母比 b 中对应字母在字母表中出现顺序更早，则认为 a 的字典序比 b 的字典序要小。

返回最终的回文字符串。

示例 1：

输入：s = "egcfe"
输出："efcfe"
解释：将 "egcfe" 变成回文字符串的最小操作次数为 1 ，修改 1 次得到的字典序最小回文字符串是 "efcfe"，只需将 'g' 改为 'f' 。

示例 2：

输入：s = "abcd"
输出："abba"
解释：将 "abcd" 变成回文字符串的最小操作次数为 2 ，修改 2 次得到的字典序最小回文字符串是 "abba" 。

示例 3：

输入：s = "seven"
输出："neven"
解释：将 "seven" 变成回文字符串的最小操作次数为 1 ，修改 1 次得到的字典序最小回文字符串是 "neven" 。

提示：

• 1 <= s.length <= 1000
• s 仅由小写英文字母组成

class Solution {
    public String makeSmallestPalindrome(String s) {
        char[] str = s.toCharArray();
        int n = str.length;
        int left = 0, right = n - 1;
        while (left < right) {
            if (str[left] != str[right]) {
                str[left] = str[right] = (char) Math.min(str[left], str[right]);
            }
            left++;
            right--;
        }
        return new String(str);
    }
}

2132 用邮票贴满网格图

2132. 用邮票贴满网格图 - 力扣（LeetCode）

差分数组 前缀和 贪心

给你一个 m x n 的二进制矩阵 grid ，每个格子要么为 0 （空）要么为 1 （被占据）。

给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中，且满足以下 限制 和 要求 ：

1. 覆盖所有 空 格子。
2. 不覆盖任何 被占据 的格子。
3. 我们可以放入任意数目的邮票。
4. 邮票可以相互有 重叠 部分。
5. 邮票不允许 旋转 。
6. 邮票必须完全在矩阵 内 。

如果在满足上述要求的前提下，可以放入邮票，请返回 true ，否则返回 false 。

示例 1：

输入：grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
输出：true
解释：我们放入两个有重叠部分的邮票（图中标号为 1 和 2），它们能覆盖所有与空格子。

示例 2：

输入：grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 
输出：false 
解释：没办法放入邮票覆盖所有的空格子，且邮票不超出网格图以外。

提示：

• m == grid.length
• n == grid[r].length
• 1 <= m, n <= 105
• 1 <= m * n <= 2 * 105
• grid[r][c] 要么是 0 ，要么是 1 。
• 1 <= stampHeight, stampWidth <= 105

class Solution {
    public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) {
        int m = grid.length;
        int n = grid[0].length;

        //计算grid二维前缀和
        int[][] s = new int[m + 1][n + 1];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] -s[i][j] + grid[i][j];
            }
        }

        //计算二维差分
        int[][] d = new int[m + 2][n + 2];
        for (int i2 = stampHeight; i2 <= m; i2++) {
            for (int j2 = stampWidth; j2 <= n; j2++) {
                int i1 = i2 - stampHeight + 1;
                int j1 = j2 - stampWidth + 1;
                if (s[i2][j2] - s[i2][j1 - 1] - s[i1 - 1][j2] + s[i1 - 1][j1 - 1] == 0) {
                    d[i1][j1]++;
                    d[i1][j2 + 1]--;
                    d[i2 + 1][j1]--;
                    d[i2 + 1][j2 + 1]++;
                }
            }
        }

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j];
                if (grid[i][j] == 0 && d[i + 1][j + 1] == 0) {
                    return false;
                }
            }
        }
        return true;
    }
}

2415 反转二叉树的奇数层

2415. 反转二叉树的奇数层 - 力扣（LeetCode）

层序遍历

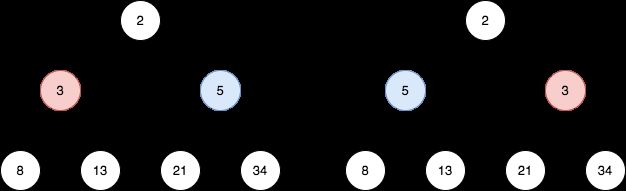
给你一棵 完美 二叉树的根节点 root ，请你反转这棵树中每个 奇数 层的节点值。

• 例如，假设第 3 层的节点值是 [2,1,3,4,7,11,29,18] ，那么反转后它应该变成 [18,29,11,7,4,3,1,2] 。

反转后，返回树的根节点。

完美 二叉树需满足：二叉树的所有父节点都有两个子节点，且所有叶子节点都在同一层。

节点的 层数 等于该节点到根节点之间的边数。

示例 1：

输入：root = [2,3,5,8,13,21,34]
输出：[2,5,3,8,13,21,34]
解释：
这棵树只有一个奇数层。
在第 1 层的节点分别是 3、5 ，反转后为 5、3 。

示例 2：

输入：root = [7,13,11]
输出：[7,11,13]
解释： 
在第 1 层的节点分别是 13、11 ，反转后为 11、13 。 

示例 3：

输入：root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
输出：[0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
解释：奇数层由非零值组成。
在第 1 层的节点分别是 1、2 ，反转后为 2、1 。
在第 3 层的节点分别是 1、1、1、1、2、2、2、2 ，反转后为 2、2、2、2、1、1、1、1 。

提示：

• 树中的节点数目在范围 [1, 214] 内
• 0 <= Node.val <= 105
• root 是一棵 完美 二叉树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode reverseOddLevels(TreeNode root) {
        Queue<TreeNode> q = new ArrayDeque<>();
        q.add(root);
        for (int i = 0; !q.isEmpty(); i++) {
            List<TreeNode> ans = new ArrayList<>();
            int n = q.size();
            while(n-- > 0) {
                TreeNode node = q.poll();
                if (i % 2 == 1) ans.add(node);
                if (node.left != null) q.add(node.left);
                if (node.right != null) q.add(node.right);
            }
            for (int l = 0, r = ans.size() - 1; l < r; l++, r--) {
                var temp = ans.get(l).val;
                ans.get(l).val = ans.get(r).val;
                ans.get(r).val = temp;
            }
        }
        return root;
    }
}

2276 统计区间中的整数数目

2276. 统计区间中的整数数目 - 力扣（LeetCode）

线段树

给你区间的 空 集，请你设计并实现满足要求的数据结构：

• **新增：**添加一个区间到这个区间集合中。
• **统计：**计算出现在 至少一个 区间中的整数个数。

实现 CountIntervals 类：

• CountIntervals() 使用区间的空集初始化对象
• void add(int left, int right) 添加区间 [left, right] 到区间集合之中。
• int count() 返回出现在 至少一个 区间中的整数个数。

**注意：**区间 [left, right] 表示满足 left <= x <= right 的所有整数 x 。

示例 1：

输入
["CountIntervals", "add", "add", "count", "add", "count"]
[[], [2, 3], [7, 10], [], [5, 8], []]
输出
[null, null, null, 6, null, 8]

解释
CountIntervals countIntervals = new CountIntervals(); // 用一个区间空集初始化对象
countIntervals.add(2, 3);  // 将 [2, 3] 添加到区间集合中
countIntervals.add(7, 10); // 将 [7, 10] 添加到区间集合中
countIntervals.count();    // 返回 6
                           // 整数 2 和 3 出现在区间 [2, 3] 中
                           // 整数 7、8、9、10 出现在区间 [7, 10] 中
countIntervals.add(5, 8);  // 将 [5, 8] 添加到区间集合中
countIntervals.count();    // 返回 8
                           // 整数 2 和 3 出现在区间 [2, 3] 中
                           // 整数 5 和 6 出现在区间 [5, 8] 中
                           // 整数 7 和 8 出现在区间 [5, 8] 和区间 [7, 10] 中
                           // 整数 9 和 10 出现在区间 [7, 10] 中

提示：

• 1 <= left <= right <= 109
• 最多调用 add 和 count 方法 总计 105 次
• 调用 count 方法至少一次

class CountIntervals:
    __slots__ = 'left', 'right', 'l', 'r', 'cnt'

    def __init__(self, l=1, r=10 ** 9):
        self.left = self.right = None
        self.l, self.r, self.cnt = l, r, 0

    def add(self, l: int, r: int) -> None:
        if self.cnt == self.r - self.l + 1:
            return
        if l <= self.l and self.r <= r:
            self.cnt = self.r - self.l + 1
            return
        mid = (self.l + self.r) // 2
        if self.left is None:
            self.left = CountIntervals(self.l, mid)
        if self.right is None:
            self.right = CountIntervals(mid + 1, self.r)
        if l <= mid:
            self.left.add(l, r)
        if mid < r:
            self.right.add(l, r)
        self.cnt = self.left.cnt + self.right.cnt

    def count(self) -> int:
        return self.cnt


# Your CountIntervals object will be instantiated and called as such:
# obj = CountIntervals()
# obj.add(left,right)
# param_2 = obj.count()

746 使用最小花费爬楼梯

746. 使用最小花费爬楼梯 - 力扣（LeetCode）

动态规划

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。
- 支付 15 ，向上爬两个台阶，到达楼梯顶部。
总花费为 15 。

示例 2：

输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。
- 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
- 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
- 支付 1 ，向上爬一个台阶，到达楼梯顶部。
总花费为 6 。

提示：

• 2 <= cost.length <= 1000
• 0 <= cost[i] <= 999

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        // int n = cost.length;
        // int[] dp = new int[n];//第i个阶梯最小花费
        // dp[0] = cost[0];
        // dp[1] = cost[1];
        // for (int i = 2; i < n; i++) {
        //     dp[i] = Math.min(dp[i - 1],dp[i - 2]) + cost[i];
        // }
        // return Math.min(dp[n - 1],dp[n -2]);
        int n = cost.length;
        //你会发现dp数组用的cost的数据，而且答案并没有涉及到cost，既然如此，直接使用cost
        for (int i = 2; i < n; i++) {
            cost[i] = Math.min(cost[i - 1],cost[i - 2]) + cost[i];
        }
        return Math.min(cost[n - 1],cost[n - 2]);
    }
}

162 寻找峰值

162. 寻找峰值 - 力扣（LeetCode）

二分查找

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

示例 1：

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。

示例 2：

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；
     或者返回索引 5， 其峰值元素为 6。

提示：

• 1 <= nums.length <= 1000
• -231 <= nums[i] <= 231 - 1
• 对于所有有效的 i 都有 nums[i] != nums[i + 1]

class Solution:
    def findPeakElement(self, nums: List[int]) -> int:
        left = -1
        right = len(nums) - 1
        while left + 1 < right:
            mid = (left + right) // 2
            if nums[mid] < nums[mid + 1]:
                left = mid
            else:
                right = mid
        return right

附模版

**原始问题：**返回有序数组中第一个≥8的数的位置 如果每个数都＜8 返回数组长度

闭区间

def lower_bound(nums: List[int], target: int) -> int:
    left = 0
    right = len(nums) - 1
    while left <= right:
        # 循环不变量 nums[left-1]=target
        # 区间左侧外面的都是 < target，区间右侧外面的都是 ≥ target
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return left

左闭右开区间

def lower_bound(nums: List[int], target: int) -> int:
    left = 0
    right = len(nums)
    while left < right:
        # 循环不变量 nums[left-1]=target
        # 区间左侧外面的都是 < target，区间右侧外面的都是 ≥ target
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid + 1 # [mid+1,right)
        else:
            right = mid # [left,mid)
    return left # 最后 left right 指向同一个位置 也可以返回 right 区间为空[)

开区间

def lower_bound(nums: List[int], target: int) -> int:
    left = -1
    right = len(nums)
    while left + 1 < right:
        # 循环不变量 nums[left]=target
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid  # (mid,right)
        else:
            right = mid # (left,mid)
    return right # left + 1

小技巧：

• ＞可以看成 ≥ x 右边的数
• ＜可以看成 ≥ x 左边的数
• ≤ 可以看成＞x

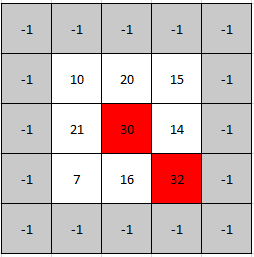
1901 寻找峰值 Ⅱ

1901. 寻找峰值 II - 力扣（LeetCode）

二分查找

一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。

给你一个 从 0 开始编号 的 m x n 矩阵 mat ，其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。

你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。

要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法

示例 1:

输入: mat = [[1,4],[3,2]]
输出: [0,1]
解释: 3 和 4 都是峰值，所以[1,0]和[0,1]都是可接受的答案。

示例 2:

输入: mat = [[10,20,15],[21,30,14],[7,16,32]]
输出: [1,1]
解释: 30 和 32 都是峰值，所以[1,1]和[2,2]都是可接受的答案。

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 500
• 1 <= mat[i][j] <= 105
• 任意两个相邻元素均不相等.

class Solution:
    def findPeakGrid(self, mat: List[List[int]]) -> List[int]:
        left = -1
        right = len(mat) - 1
        while left + 1 < right:
            i = (left + right) // 2
            mx = max(mat[i])
            if mx > mat[i + 1][mat[i].index(mx)]:
                right = i
            else:
                left = i
        i = right
        return [i, mat[i].index(max(mat[i]))]

2828 判别首字母缩略词

2828. 判别首字母缩略词 - 力扣（LeetCode）

简单模拟

给你一个字符串数组 words 和一个字符串 s ，请你判断 s 是不是 words 的 首字母缩略词 。

如果可以按顺序串联 words 中每个字符串的第一个字符形成字符串 s ，则认为 s 是 words 的首字母缩略词。例如，"ab" 可以由 ["apple", "banana"] 形成，但是无法从 ["bear", "aardvark"] 形成。

如果 s 是 words 的首字母缩略词，返回 true ；否则，返回 false 。

示例 1：

输入：words = ["alice","bob","charlie"], s = "abc"
输出：true
解释：words 中 "alice"、"bob" 和 "charlie" 的第一个字符分别是 'a'、'b' 和 'c'。因此，s = "abc" 是首字母缩略词。 

示例 2：

输入：words = ["an","apple"], s = "a"
输出：false
解释：words 中 "an" 和 "apple" 的第一个字符分别是 'a' 和 'a'。
串联这些字符形成的首字母缩略词是 "aa" 。
因此，s = "a" 不是首字母缩略词。

示例 3：

输入：words = ["never","gonna","give","up","on","you"], s = "ngguoy"
输出：true
解释：串联数组 words 中每个字符串的第一个字符，得到字符串 "ngguoy" 。
因此，s = "ngguoy" 是首字母缩略词。 

提示：

• 1 <= words.length <= 100
• 1 <= words[i].length <= 10
• 1 <= s.length <= 100
• words[i] 和 s 由小写英文字母组成

class Solution {
    public boolean isAcronym(List<String> words, String s) {
        if (words.size() != s.length()) {
            return false;
        }
        for (int i = 0; i < s.length(); i++) {
            if (words.get(i).charAt(0) != s.charAt(i)) {
                return false;
            }
        }
        return true;
    }
}

2866 美丽塔Ⅱ

2866. 美丽塔 II - 力扣（LeetCode）

前后缀分解 单调栈

给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。

你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ，高度为 heights[i] 。

如果以下条件满足，我们称这些塔是 美丽 的：

1. 1 <= heights[i] <= maxHeights[i]
2. heights 是一个 山脉 数组。

如果存在下标 i 满足以下条件，那么我们称数组 heights 是一个 山脉 数组：

• 对于所有 0 < j <= i ，都有 heights[j - 1] <= heights[j]
• 对于所有 i <= k < n - 1 ，都有 heights[k + 1] <= heights[k]

请你返回满足 美丽塔 要求的方案中，高度和的最大值 。

示例 1：

输入：maxHeights = [5,3,4,1,1]
输出：13
解释：和最大的美丽塔方案为 heights = [5,3,3,1,1] ，这是一个美丽塔方案，因为：
- 1 <= heights[i] <= maxHeights[i]  
- heights 是个山脉数组，峰值在 i = 0 处。
13 是所有美丽塔方案中的最大高度和。

示例 2：

输入：maxHeights = [6,5,3,9,2,7]
输出：22
解释： 和最大的美丽塔方案为 heights = [3,3,3,9,2,2] ，这是一个美丽塔方案，因为：
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山脉数组，峰值在 i = 3 处。
22 是所有美丽塔方案中的最大高度和。

示例 3：

输入：maxHeights = [3,2,5,5,2,3]
输出：18
解释：和最大的美丽塔方案为 heights = [2,2,5,5,2,2] ，这是一个美丽塔方案，因为：
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山脉数组，最大值在 i = 2 处。
注意，在这个方案中，i = 3 也是一个峰值。
18 是所有美丽塔方案中的最大高度和。

提示：

• 1 <= n == maxHeights <= 105
• 1 <= maxHeights[i] <= 109

class Solution:
    def maximumSumOfHeights(self, maxHeights: List[int]) -> int:
        n = len(maxHeights)
        suf = [0] * (n + 1)
        st = [n]
        s = 0
        for i in range(n - 1, -1, -1):
            x = maxHeights[i]
            while len(st) > 1 and x <= maxHeights[st[-1]]:
                j = st.pop()
                s -= maxHeights[j] * (st[-1] - j)
            s += x * (st[-1] - i)
            suf[i] = s
            st.append(i)
        ans = s
        st = [-1]
        pre = 0
        for i, x in enumerate(maxHeights):
            while len(st) > 1 and x <= maxHeights[st[-1]]:
                j = st.pop()
                pre -= maxHeights[j] * (j - st[-1])
            pre += x * (i - st[-1])
            ans = max(ans, pre + suf[i + 1])
            st.append(i)
        return ans 

1671 得到山行数组的最少删除次数

1671. 得到山形数组的最少删除次数 - 力扣（LeetCode）

前后缀分解 最长递增子序列 二分查找

我们定义 arr 是 山形数组 当且仅当它满足：

• arr.length >= 3
• 存在某个下标 i（从 0 开始） 满足 0 < i < arr.length - 1且：
  • arr[0] < arr[1] < ... < arr[i - 1] < arr[i]
  • arr[i] > arr[i + 1] > ... > arr[arr.length - 1]

给你整数数组 nums ，请你返回将 nums 变成 山形状数组 的 最少 删除次数。

示例 1：

输入：nums = [1,3,1]
输出：0
解释：数组本身就是山形数组，所以我们不需要删除任何元素。

示例 2：

输入：nums = [2,1,1,5,6,2,3,1]
输出：3
解释：一种方法是将下标为 0，1 和 5 的元素删除，剩余元素为 [1,5,6,3,1] ，是山形数组。

提示：

• 3 <= nums.length <= 1000
• 1 <= nums[i] <= 109
• 题目保证 nums 删除一些元素后一定能得到山形数组。

class Solution:
    def minimumMountainRemovals(self, nums: List[int]) -> int:
        n = len(nums)
        suf = [0] * n
        g = []
        for i in range(n - 1, 0, -1):
            x = nums[i]
            j = bisect_left(g, x)
            if j == len(g):
                g.append(x)
            else:
                g[j] = x
            suf[i] = j + 1
        mx = 0
        g = []
        for i, x in enumerate(nums):
            j = bisect_left(g, x)
            if j == len(g):
                g.append(x)
            else:
                g[j] = x
            pre = j + 1
            if pre >= 2 and suf[i] >= 2:
                mx = max(mx, pre + suf[i] - 1)
        return n - mx

1962 移除石子使总数最小

1962. 移除石子使总数最小 - 力扣（LeetCode）

堆

给你一个整数数组 piles ，数组 下标从 0 开始 ，其中 piles[i] 表示第 i 堆石子中的石子数量。另给你一个整数 k ，请你执行下述操作 恰好 k 次：

• 选出任一石子堆 piles[i] ，并从中 移除 floor(piles[i] / 2) 颗石子。

**注意：**你可以对 同一堆 石子多次执行此操作。

返回执行 k 次操作后，剩下石子的 最小 总数。

floor(x) 为 小于 或 等于 x 的 最大 整数。（即，对 x 向下取整）。

示例 1：

输入：piles = [5,4,9], k = 2
输出：12
解释：可能的执行情景如下：
- 对第 2 堆石子执行移除操作，石子分布情况变成 [5,4,5] 。
- 对第 0 堆石子执行移除操作，石子分布情况变成 [3,4,5] 。
剩下石子的总数为 12 。

示例 2：

输入：piles = [4,3,6,7], k = 3
输出：12
解释：可能的执行情景如下：
- 对第 2 堆石子执行移除操作，石子分布情况变成 [4,3,3,7] 。
- 对第 3 堆石子执行移除操作，石子分布情况变成 [4,3,3,4] 。
- 对第 0 堆石子执行移除操作，石子分布情况变成 [2,3,3,4] 。
剩下石子的总数为 12 。

提示：

• 1 <= piles.length <= 105
• 1 <= piles[i] <= 104
• 1 <= k <= 105

class Solution {
    public int minStoneSum(int[] piles, int k) {
        //选出数组中最大的数，移除它的一半
        heapify(piles);
        while (k-- > 0 && piles[0] > 0) {
            piles[0] -= piles[0] / 2;
            sink(piles, 0);
        }
        int ans = 0;
        for (int x : piles) {
            ans += x;
        }
        return ans;
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    private void sink(int[] h, int i) {
        int n = h.length;
        while (2 * i + 1 < n) {
            int j = 2 * i + 1;
            if (j + 1 < n && h[j + 1] > h[j]) {
                j++;
            }
            if (h[j] <= h[i]) {
                break;
            }
            swap(h, i, j);
            i = j;
        }
    }

    private void heapify(int[] h) {
        for (int i = h.length / 2 - 1; i >= 0; i--) {
            sink(h, i);
        }
    }
}

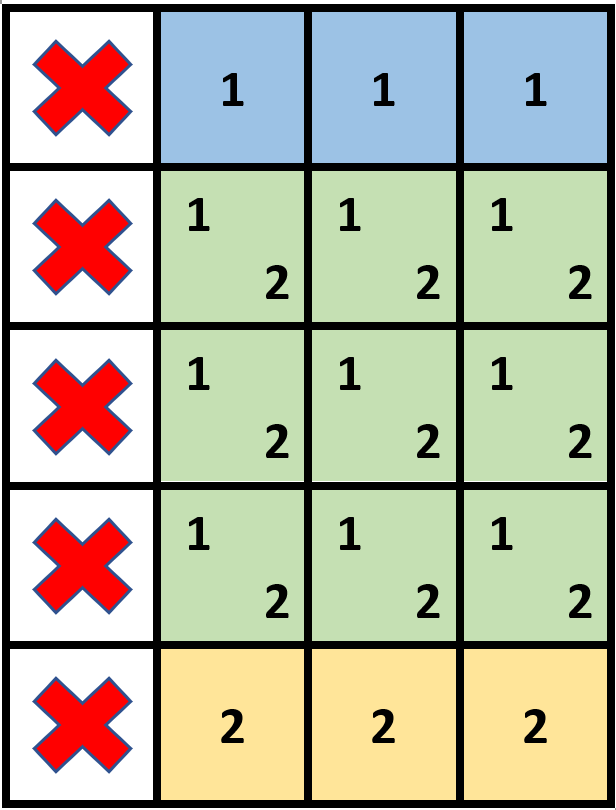
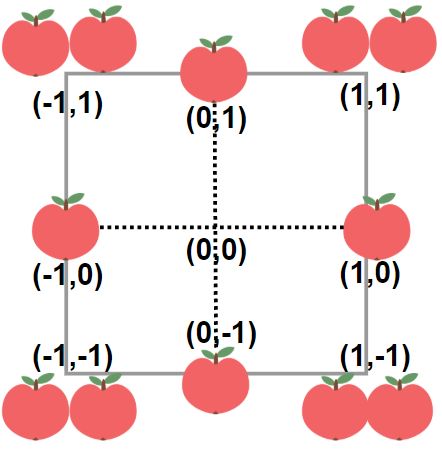
1954 收集足够苹果的最小花园周长

1954. 收集足够苹果的最小花园周长 - 力扣（LeetCode）

暴力枚举 数论 二分查找

给你一个用无限二维网格表示的花园，每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| + |j| 个苹果。

你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ，且每条边都与两条坐标轴之一平行。

给你一个整数 neededApples ，请你返回土地的 最小周长 ，使得 至少 有 neededApples 个苹果在土地 里面或者边缘上。

|x| 的值定义为：

• 如果 x >= 0 ，那么值为 x
• 如果 x < 0 ，那么值为 -x

示例 1：

输入：neededApples = 1
输出：8
解释：边长长度为 1 的正方形不包含任何苹果。
但是边长为 2 的正方形包含 12 个苹果（如上图所示）。
周长为 2 * 4 = 8 。

示例 2：

输入：neededApples = 13
输出：16

示例 3：

输入：neededApples = 1000000000
输出：5040

提示：

• 1 <= neededApples <= 1015

class Solution {
    public long minimumPerimeter(long neededApples) {
        long n = (long) Math.cbrt(neededApples / 4.0);
        while(2 * n * (n + 1) * (2 * n + 1) < neededApples) {
            n++;
        }
        return 8 * n;
    }
}

1276 不浪费原料的汉堡制作方案

1276. 不浪费原料的汉堡制作方案 - 力扣（LeetCode）

数论

圣诞活动预热开始啦，汉堡店推出了全新的汉堡套餐。为了避免浪费原料，请你帮他们制定合适的制作计划。

给你两个整数 tomatoSlices 和 cheeseSlices，分别表示番茄片和奶酪片的数目。不同汉堡的原料搭配如下：

• **巨无霸汉堡：**4 片番茄和 1 片奶酪
• **小皇堡：**2 片番茄和 1 片奶酪

请你以 [total_jumbo, total_small]（[巨无霸汉堡总数，小皇堡总数]）的格式返回恰当的制作方案，使得剩下的番茄片 tomatoSlices 和奶酪片 cheeseSlices 的数量都是 0。

如果无法使剩下的番茄片 tomatoSlices 和奶酪片 cheeseSlices 的数量为 0，就请返回 []。

示例 1：

输入：tomatoSlices = 16, cheeseSlices = 7
输出：[1,6]
解释：制作 1 个巨无霸汉堡和 6 个小皇堡需要 4*1 + 2*6 = 16 片番茄和 1 + 6 = 7 片奶酪。不会剩下原料。

示例 2：

输入：tomatoSlices = 17, cheeseSlices = 4
输出：[]
解释：只制作小皇堡和巨无霸汉堡无法用光全部原料。

示例 3：

输入：tomatoSlices = 4, cheeseSlices = 17
输出：[]
解释：制作 1 个巨无霸汉堡会剩下 16 片奶酪，制作 2 个小皇堡会剩下 15 片奶酪。

示例 4：

输入：tomatoSlices = 0, cheeseSlices = 0
输出：[0,0]

示例 5：

输入：tomatoSlices = 2, cheeseSlices = 1
输出：[0,1]

提示：

• 0 <= tomatoSlices <= 10^7
• 0 <= cheeseSlices <= 10^7

class Solution:
    def numOfBurgers(self, tomatoSlices: int, cheeseSlices: int) -> List[int]:
        x = (tomatoSlices - 2 * cheeseSlices) / 2
        y = (4 * cheeseSlices - tomatoSlices) / 2
        if x < 0 or y < 0 or tomatoSlices % 2 != 0:
            return []
        return [int(x), int(y)]

1349 参加考试的最大学生数

1349. 参加考试的最大学生数 - 力扣（LeetCode）

动态规划 状态压缩DP 位运算

给你一个 m * n 的矩阵 seats 表示教室中的座位分布。如果座位是坏的（不可用），就用 '#' 表示；否则，用 '.' 表示。

学生可以看到左侧、右侧、左上、右上这四个方向上紧邻他的学生的答卷，但是看不到直接坐在他前面或者后面的学生的答卷。请你计算并返回该考场可以容纳的同时参加考试且无法作弊的 最大 学生人数。

学生必须坐在状况良好的座位上。

示例 1：

输入：seats = [["#",".","#","#",".","#"],
              [".","#","#","#","#","."],
              ["#",".","#","#",".","#"]]
输出：4
解释：教师可以让 4 个学生坐在可用的座位上，这样他们就无法在考试中作弊。 

示例 2：

输入：seats = [[".","#"],
              ["#","#"],
              ["#","."],
              ["#","#"],
              [".","#"]]
输出：3
解释：让所有学生坐在可用的座位上。

示例 3：

输入：seats = [["#",".",".",".","#"],
              [".","#",".","#","."],
              [".",".","#",".","."],
              [".","#",".","#","."],
              ["#",".",".",".","#"]]
输出：10
解释：让学生坐在第 1、3 和 5 列的可用座位上。

提示：

• seats 只包含字符 '.' 和``'#'
• m == seats.length
• n == seats[i].length
• 1 <= m <= 8
• 1 <= n <= 8

class Solution {
    public int maxStudents(char[][] seats) {
        int m = seats.length;
        int n = seats[0].length;
        int[] a = new int[m];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (seats[i][j] == '.') {
                    a[i] |= 1 << j;
                }
            }
        }
        int[][] cache = new int[m][1 << n];
        for (var row : cache) {
            Arrays.fill(row, -1);
        }
        return dfs(m - 1, a[m - 1], cache, a);
    }

    public int dfs(int i, int j, int[][] cache, int[] a) {
        if (cache[i][j] != -1) {
            return cache[i][j];
        }
        if (i == 0) {
            if (j == 0) {
                return 0;
            }
            int lb = j & -j;
            return cache[i][j] = dfs(i, j & ~(lb * 3), cache, a) + 1;
        }
        int res = dfs(i - 1, a[i - 1], cache, a);
        for (int s = j; s > 0; s = (s - 1) & j) {
            if ((s & (s >> 1)) == 0) {
                int t = a[i - 1] & ~(s << 1 | s >> 1);
                res = Math.max(res, dfs(i - 1, t, cache, a) + Integer.bitCount(s));
            }
        }
        return cache[i][j] = res;
    }
}

2660 保龄球游戏的获胜者

2660. 保龄球游戏的获胜者 - 力扣（LeetCode）

模拟

给你两个下标从 0 开始的整数数组 player1 和 player2 ，分别表示玩家 1 和玩家 2 击中的瓶数。

保龄球比赛由 n 轮组成，每轮的瓶数恰好为 10 。

假设玩家在第 i 轮中击中 xi 个瓶子。玩家第 i 轮的价值为：

• 如果玩家在该轮的前两轮的任何一轮中击中了 10 个瓶子，则为 2xi 。
• 否则，为 xi 。

玩家的得分是其 n 轮价值的总和。

返回

• 如果玩家 1 的得分高于玩家 2 的得分，则为 1 ；
• 如果玩家 2 的得分高于玩家 1 的得分，则为 2 ；
• 如果平局，则为 0 。

示例 1：

输入：player1 = [4,10,7,9], player2 = [6,5,2,3]
输出：1
解释：player1 的得分是 4 + 10 + 2*7 + 2*9 = 46 。
player2 的得分是 6 + 5 + 2 + 3 = 16 。
player1 的得分高于 player2 的得分，所以 play1 在比赛中获胜，答案为 1 。

示例 2：

输入：player1 = [3,5,7,6], player2 = [8,10,10,2]
输出：2
解释：player1 的得分是 3 + 5 + 7 + 6 = 21 。
player2 的得分是 8 + 10 + 2*10 + 2*2 = 42 。
player2 的得分高于 player1 的得分，所以 play2 在比赛中获胜，答案为 2 。

示例 3：

输入：player1 = [2,3], player2 = [4,1]
输出：0
解释：player1 的得分是 2 + 3 = 5 。
player2 的得分是 4 + 1 = 5 。
player1 的得分等于 player2 的得分，所以这一场比赛平局，答案为 0 。

提示：

• n == player1.length == player2.length
• 1 <= n <= 1000
• 0 <= player1[i], player2[i] <= 10

class Solution {
    public int isWinner(int[] player1, int[] player2) {
        int sum1 = 0, sum2 = 0;
        for (int i = 0; i < player1.length; i++) {
            if ((i >= 1 && player1[i - 1] == 10) || (i >= 2 && player1[i - 2] == 10)) {
                sum1 += 2 * player1[i];
            } else {
                sum1 += player1[i];
            }
        }
        for (int i = 0; i < player2.length; i++) {
            if ((i >= 1 && player2[i - 1] == 10) || (i >= 2 && player2[i - 2] == 10)) {
                sum2 += 2 * player2[i];
            } else {
                sum2 += player2[i];
            }
        }
        if (sum1 == sum2) {
            return 0;
        }
        return sum1 > sum2 ? 1 : 2;
    }
}

2735 收集巧克力

2735. 收集巧克力 - 力扣（LeetCode）

枚举

给你一个长度为 n 、下标从 0 开始的整数数组 nums ，表示收集不同巧克力的成本。每个巧克力都对应一个不同的类型，最初，位于下标 i 的巧克力就对应第 i 个类型。

在一步操作中，你可以用成本 x 执行下述行为：

• 同时修改所有巧克力的类型，将巧克力的类型 ith 修改为类型 ((i + 1) mod n)th。

假设你可以执行任意次操作，请返回收集所有类型巧克力所需的最小成本。

示例 1：

输入：nums = [20,1,15], x = 5
输出：13
解释：最开始，巧克力的类型分别是 [0,1,2] 。我们可以用成本 1 购买第 1 个类型的巧克力。
接着，我们用成本 5 执行一次操作，巧克力的类型变更为 [1,2,0] 。我们可以用成本 1 购买第 2 个类型的巧克力。
然后，我们用成本 5 执行一次操作，巧克力的类型变更为 [2,0,1] 。我们可以用成本 1 购买第 0 个类型的巧克力。
因此，收集所有类型的巧克力需要的总成本是 (1 + 5 + 1 + 5 + 1) = 13 。可以证明这是一种最优方案。

示例 2：

输入：nums = [1,2,3], x = 4
输出：6
解释：我们将会按最初的成本收集全部三个类型的巧克力，而不需执行任何操作。因此，收集所有类型的巧克力需要的总成本是 1 + 2 + 3 = 6 。

提示：

• 1 <= nums.length <= 1000
• 1 <= nums[i] <= 109
• 1 <= x <= 109

class Solution {
    public long minCost(int[] nums, int x) {
        int n = nums.length;
        long[] s = new long[n];
        for (int i = 0; i < n; i++) {
            s[i] = (long) i * x;
        }
        for (int i = 0; i < n; i++) {
            int mn = nums[i];
            for (int j = i; j < n + i; j++) {
                mn = Math.min(mn, nums[j % n]);
                s[j - i] += mn;
            }
        }
        long ans = Long.MAX_VALUE;
        for (long v : s) {
            ans = Math.min(ans, v);
        }
        return ans;
    }
}

2706 购买两块巧克力

2706. 购买两块巧克力 - 力扣（LeetCode）

枚举

给你一个整数数组 prices ，它表示一个商店里若干巧克力的价格。同时给你一个整数 money ，表示你一开始拥有的钱数。

你必须购买 恰好 两块巧克力，而且剩余的钱数必须是 非负数 。同时你想最小化购买两块巧克力的总花费。

请你返回在购买两块巧克力后，最多能剩下多少钱。如果购买任意两块巧克力都超过了你拥有的钱，请你返回 money 。注意剩余钱数必须是非负数。

示例 1：

输入：prices = [1,2,2], money = 3
输出：0
解释：分别购买价格为 1 和 2 的巧克力。你剩下 3 - 3 = 0 块钱。所以我们返回 0 。

示例 2：

输入：prices = [3,2,3], money = 3
输出：3
解释：购买任意 2 块巧克力都会超过你拥有的钱数，所以我们返回 3 。

提示：

• 2 <= prices.length <= 50
• 1 <= prices[i] <= 100
• 1 <= money <= 100

class Solution {
    public int buyChoco(int[] prices, int money) {
        int mn1 = Integer.MAX_VALUE, mn2 = Integer.MAX_VALUE;
        for (int p : prices) {
            if (p < mn1) {
                mn2 = mn1;
                mn1 = p;
            } else if (p < mn2) {
                mn2 = p;
            }
        }
        if (mn1 + mn2 > money) {
            return money;
        }
        return money - mn1 - mn2;
    }
}

1185 一周中的第几天

1185. 一周中的第几天 - 力扣（LeetCode）

模拟

给你一个日期，请你设计一个算法来判断它是对应一周中的哪一天。

输入为三个整数：day、month 和 year，分别表示日、月、年。

您返回的结果必须是这几个值中的一个 {"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"}。

示例 1：

输入：day = 31, month = 8, year = 2019
输出："Saturday"

示例 2：

输入：day = 18, month = 7, year = 1999
输出："Sunday"

示例 3：

输入：day = 15, month = 8, year = 1993
输出："Sunday"

提示：

• 给出的日期一定是在 1971 到 2100 年之间的有效日期。

class Solution {
    private String[] tempDay = new String[]{"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"};
    private int[] tempDays = new int[]{31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

    public String dayOfTheWeek(int day, int month, int year) {
        int ans = 4; // 1970最后一天是星期四
        for (int i = 1971; i < year; i++) {
            boolean isLeap = ((i % 4 == 0 && i % 100 != 0) || i % 400 == 0);
            ans += isLeap ? 366 : 365;
        }
        for (int i = 1; i < month; i++) {
            ans += tempDays[i - 1];
            if (i == 2 && ((year % 4 == 0 && year % 100 != 0) || year % 400 == 0)) {
                ans++;
            }
        }
        ans += day;
        return tempDay[ans % 7];
    }
}

库函数

import java.util.Calendar;
import java.text.SimpleDateFormat;

class Solution {
    private static final Calendar calendar = Calendar.getInstance();
    private static final SimpleDateFormat weekFormat = new SimpleDateFormat("EEEE");

    public String dayOfTheWeek(int day, int month, int year) {
        calendar.set(year, month - 1, day);
        return weekFormat.format(calendar.getTime());
    }
}

class Solution:
    def dayOfTheWeek(self, day: int, month: int, year: int) -> str:
        return datetime.datetime(year, month, day).strftime("%A")

1154 一年中的第几天

1154. 一年中的第几天 - 力扣（LeetCode）

模拟

给你一个字符串 date ，按 YYYY-MM-DD 格式表示一个 现行公元纪年法 日期。返回该日期是当年的第几天。

示例 1：

输入：date = "2019-01-09"
输出：9
解释：给定日期是2019年的第九天。

示例 2：

输入：date = "2019-02-10"
输出：41

提示：

• date.length == 10
• date[4] == date[7] == '-'，其他的 date[i] 都是数字
• date 表示的范围从 1900 年 1 月 1 日至 2019 年 12 月 31 日

class Solution {
    private static int[] Days = new int[]{31,28,31,30,31,30,31,31,30,31,30,31};
    private static int[] f = new int[13];
    static {
        for (int i = 1; i <= 12; i++) {
            f[i] = f[i - 1] + Days[i - 1];
        }
    }

    public int dayOfYear(String date) {
        String[] s = date.split("-");
        int year = Integer.parseInt(s[0]), month = Integer.parseInt(s[1]), day = Integer.parseInt(s[2]);
        boolean isLeap = (year % 4 == 0 && year % 100 != 0) || year % 400 == 0;
        int res = month > 2 && isLeap ? f[month - 1] + 1 : f[month - 1];
        return res + day;
    }
}

库函数

import java.time.LocalDate;
import java.time.format.DateTimeFormatter;

class Solution {
    private static final DateTimeFormatter f = DateTimeFormatter.ofPattern("yyyy-MM-dd");

    public int dayOfYear(String date) {
        return LocalDate.parse(date, f).getDayOfYear();
    }
}

class Solution:
    def dayOfYear(self, date: str) -> int:
        return datetime.datetime.strptime(date, "%Y-%m-%d").timetuple().tm_yday