南京邮电大学算法与数据结构设计:文本的加密与解密、校园导航系统
作者:
由于文件数量过多,逐个上传较为繁琐,所以文章中上传的代码只是部分主要的结构,需要源码的小伙伴可以去我的Github上搜索,地址为:GitHub - xxz1314520/Algorithm-and-Program-Design-of-NJUPT: 这是我在南京邮电大学计算机学院所开设的课程《算法与数据结构设计》写的项目
A.文本的加密和解密
一、课题内容和要求
设计要求:设计对已知文本进行加密和解密程序,要求界面友好。给出字母加密映射表;包括加密和解密功能,加密功能是将导入的文本进行加密后输出;解密功能是将已加密的文件进行解密后输出。
二、课题需求分析
A课题目标“文本的加密与解密”的功能框架图如图1所示。
图1 功能框架图
(1)对于文本的加密和解密需求;
(2)提供加解密算法选择多样性;
(3)支持多次加密多次解密需求;
(4)简洁明了的界面和发布版本的exe文件格式。
三、课题相关数据结构及算法设计
1主要数据结构
(1)转轮加解密算法
class WheelEncryption
{
private:
int flag1,flag2; //转轮转动标志位
int slowL[26],slowR[26]; //慢轮子
int midL[26],midR[26]; //中轮子
int fastL[26],fastR[26]; //快轮子
char input[27],output[27]; //将待输出密文下标转化成字符的参照表
public:
string plaintext; //明文
string cipertext; //密文
};
(2)AES加解密算法
static const unsigned char sbox[256]; //S盒矩阵
static const unsigned char contrary_sbox[256]; //逆向S盒矩阵
class AES
{
private:
string plaintext; //明文
string cipertext; //密文
unsigned char pt[17], key[17]; //定义明文pt,密钥key
public:
int temp; //下标
};
(3)RSA加解密算法
class RSA
{
private:
int p = 17;
int q = 19; // 选择两个不同的素数p和q
int n = p * q; // 计算n
int phi = (p - 1) * (q - 1); // 计算phi(n)
int e = 7; // 选择一个与phi(n)互质的数e
public:
string plaintext; //明文
string cipertext; //密文
};2 .主要算法流程
-
转轮机加解密算法:
转轮密码机由多个转轮构成,每个转轮旋转的速度都不一样,比如有3个转轮,分别标号为1,2,3,其中1号转轮转动26个字母后,2号转轮就转动一个字母,当2号转轮转动26个字母后,3号转轮就转动1个字母。因此,当转轮密码机转动26^3次后,所有转轮恢复到初始状态,即3个转轮密码机的一个周期长度为26^3(17576)的多表代换密码。解密流程:将密文消息拆分为单个字母。对每个字母执行与加密步骤相同的操作,但是使用相同的配置和起始位置。解密得到的字母即为明文字母。
流程图如图2所示。
图2 转轮机加解密流程图
(2)AES加解密算法:
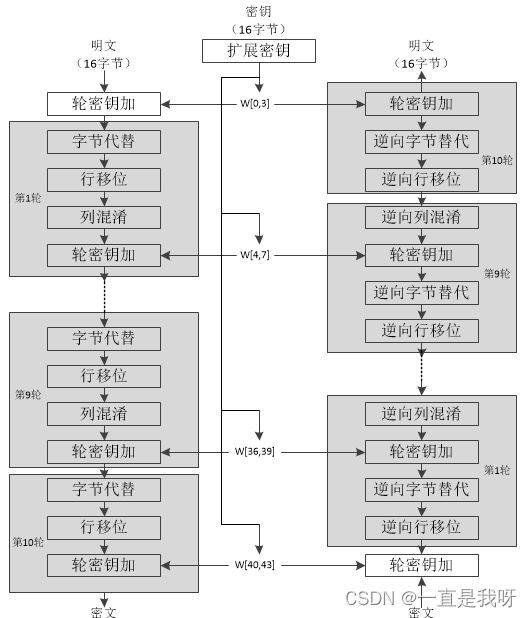
根据输入的密钥,生成一系列的轮密钥(Round Keys)。轮密钥的数量取决于密钥长度和加密轮数。初始轮(Initial Round):将输入的明文分成块,通常每个块的大小为128位(16字节)。将明文块与第一个轮密钥进行异或运算。轮运算(Rounds):迭代执行多轮相同的步骤,每轮包括四个步骤:字节替换(SubBytes)、行移位(ShiftRows)、列混淆(MixColumns)、轮密钥加(AddRoundKey)。字节替换(SubBytes):将明文块中的每个字节替换为S盒表中对应的字节。行移位(ShiftRows):按照特定规则对明文块中的每一行进行循环移位操作。列混淆(MixColumns):对明文块中的每一列进行线性变换,混淆字节的位置。轮密钥加(AddRoundKey):将轮密钥与当前明文块进行异或运算。最后一轮(Final Round):进行与其他轮相同的步骤,但省略列混淆(MixColumns)操作。最后的结果即为密文块。
解密时,与加密过程类似,但使用逆操作进行逆向操作,包括:密钥扩展(Key Expansion):生成与加密过程相同的轮密钥。初始轮(Initial Round):将密文块与最后一个轮密钥进行异或运算。逆向轮运算(Inverse Rounds):迭代执行多轮相同的逆向步骤,包括逆向字节替换、逆向行移位、逆向列混淆和轮密钥加。最后一轮(Final Round):进行与其他逆向轮相同的步骤,但省略逆向列混淆操作。解密的最后结果即为原始明文块。
流程图如图3所示。
图3 AES加解密流程图
(3)RSA加解密算法:
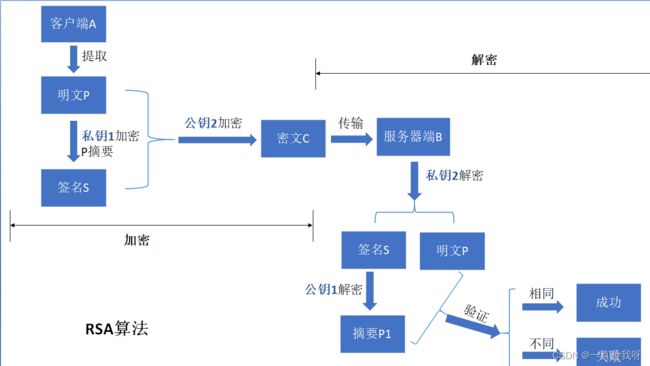
RSA(Rivest-Shamir-Adleman)是一种非对称密钥加密算法,以下是RSA算法的基本流程:。
1. 密钥生成:选择两个不同的质数p和q。计算模数 n = p * q。计算欧拉函数值 φ(n) = (p - 1) * (q - 1)。选择一个整数 e,使得 1 < e < φ(n) 并且 e 与 φ(n) 互质,即它们没有公共的因子。计算e的乘法逆元 d,满足 (d * e) mod φ(n) = 1。公钥为 (n, e),私钥为 (n, d)。
2. 加密:将明文转换为对应的整数值 m,满足 0 ≤ m < n。计算密文 c = (m^e) mod nZ密文 c 即为加密后的结果。
3. 解密: - 接收到密文 c。使用私钥中的模数 n 和指数 d,计算解密后的明文值 m = (c^d) mod n。明文 m 即为解密的结果。
流程图如图4所示。
图4 RSA加解密流程图
四、源程序代码
课题源代码:
public:
void roatewheel(int wheel[26]) {
int temp = wheel[25];
for (int i = 24; i >= 0; i--) {
wheel[i + 1] = wheel[i]; }
wheel[0] = temp % 26; // 限制索引值在合法范围内
return; }
int searchindex(int wheel[26], int figure)
{ //查找整型类型的轮子的下标,并返回下标
for (int i = 0; i < 26; i++) {
if (wheel[i] == figure)
return i; }
printf("查询失败!");
return ERROR;}
int searchindex(char wheel[27], char figure)
{ //查找字符串型的轮子的小标,并返回下标
for (int i = 0; i < 26; i++)
{if (wheel[i] == figure)
return i;}
printf("查询失败!");
return ERROR;}
void OutputCipertext(string plaintext){//输出密文
int len = plaintext.length();
int ind1, ind2, ind3, ind4; //定义四个下标量
for (int i = 0; i < len; i++) {
ind1 = searchindex(input, plaintext[i]); //明文字符转化为对应数字,并返回数字下标
ind2 = searchindex(slowR, slowL[ind1]); //进入中轮子
ind3 = searchindex(midR, midL[ind2]); //进入快轮子
ind4 = searchindex(fastR, fastL[ind3]); //返回密文字符对应的下标
flag1++; //输出字符对应的密文
cout << input[ind4];
roatewheel(fastL); //每输出一位,快轮子转动一次
roatewheel(fastR);
if (flag1 % 26 == 0 && flag1 != 0) { //快轮子每转动26次,中轮子转动一次
roatewheel(midL);
roatewheel(midR);
flag2++;}
if (flag2 % 26 == 0 && flag2 != 0) {//中轮子每转动26次,慢轮子转动一次
roatewheel(slowL);
roatewheel(slowR); }}
flag1 = flag2 = 0; //解密结束,标志位初始化为0
plaintext = input[ind4];}
void OutputPlaintext(string cipertext){ //解密密文
int len = cipertext.length();
int ind1, ind2, ind3, ind4;
for (int i = 0; i < len; i++) {
ind1 = searchindex(output, cipertext[i]);
ind2 = searchindex(fastL, fastR[ind1]);
ind3 = searchindex(midL, midR[ind2]);
ind4 = searchindex(slowL, slowR[ind3]);
flag1++;
roatewheel(fastL);
roatewheel(fastR);
if (flag1 % 26 == 0 && flag1 != 0) {
roatewheel(midL);
roatewheel(midR);
flag2++;}
if (flag2 % 26 == 0 && flag2 != 0) {roatewheel(slowL);
roatewheel(slowR);}
cout << input[ind4]; }
flag1 = flag2 = 0;
};
class AES
{
Public:
static unsigned char x2time(unsigned char x){ //定义有限域*2乘法
if (x & 0x80){return (((x << 1) ^ 0x1B) & 0xFF);}
return x << 1;}
static unsigned char x3time(unsigned char x){ //定义有限域*3乘法
return (x2time(x) ^ x);}
static unsigned char x4time(unsigned char x){ //定义有限域*4乘法
return (x2time(x2time(x)));}
static unsigned char x8time(unsigned char x){ //定义有限域*8乘法
return (x2time(x2time(x2time(x))));}
static unsigned char x9time(unsigned char x){ //定义有限域*9乘法
return (x8time(x) ^ x);}
static unsigned char xBtime(unsigned char x){ //定义有限域*B乘法
return (x8time(x) ^ x2time(x) ^ x);}
static unsigned char xDtime(unsigned char x){ //定义有限域*D乘法
return (x8time(x) ^ x4time(x) ^ x);}
static unsigned char xEtime(unsigned char x){ //定义有限域*E乘法
return (x8time(x) ^ x4time(x) ^ x2time(x));}
static void MixColumns(unsigned char* col){ //定义列混合操作
unsigned char tmp[4], xt[4];
int i;
for (i = 0; i < 4; i++, col += 4){ //col代表一列的基地址,col+4:下一列的基地址
//xt[n]代表*2 xt[n]^col[n]代表*3 col[n]代表*1
tmp[0] = x2time(col[0]) ^ x3time(col[1]) ^ col[2] ^ col[3]; //2 3 1 1
tmp[1] = col[0] ^ x2time(col[1]) ^ x3time(col[2]) ^ col[3]; //1 2 3 1
tmp[2] = col[0] ^ col[1] ^ x2time(col[2]) ^ x3time(col[3]); //1 1 2 3
tmp[3] = x3time(col[0]) ^ col[1] ^ col[2] ^ x2time(col[3]); //3 1 1 2
//修改后的值 直接在原矩阵上修改
col[0] = tmp[0];
col[1] = tmp[1];
col[2] = tmp[2];
col[3] = tmp[3];}}
//定义逆向列混淆
static void Contrary_MixColumns(unsigned char* col){
unsigned char tmp[4];
unsigned char xt2[4];//colx2
unsigned char xt4[4];//colx4
unsigned char xt8[4];//colx8
int x;
for (x = 0; x < 4; x++, col += 4){
tmp[0] = xEtime(col[0]) ^ xBtime(col[1]) ^ xDtime(col[2]) ^ x9time(col[3]);
tmp[1] = x9time(col[0]) ^ xEtime(col[1]) ^ xBtime(col[2]) ^ xDtime(col[3]);
tmp[2] = xDtime(col[0]) ^ x9time(col[1]) ^ xEtime(col[2]) ^ xBtime(col[3]);
tmp[3] = xBtime(col[0]) ^ xDtime(col[1]) ^ x9time(col[2]) ^ xEtime(col[3]);
col[0] = tmp[0];
col[1] = tmp[1];
col[2] = tmp[2];
col[3] = tmp[3];}}
//定义行移位操作:行左循环移位
static void ShiftRows(unsigned char* col){ //正向行移位
unsigned char t;//左移1位
t = col[1]; col[1] = col[5]; col[5] = col[9]; col[9] = col[13]; col[13] = t;
//左移2位,交换2次数字来实现
t = col[2]; col[2] = col[10]; col[10] = t;
t = col[6]; col[6] = col[14]; col[14] = t;
//左移3位,相当于右移1次
t = col[15]; col[15] = col[11]; col[11] = col[7]; col[7] = col[3]; col[3] = t;
//第4行不移位}
//逆向行移位
static void Contrary_ShiftRows(unsigned char* col){
unsigned char t;
t = col[13]; col[13] = col[9]; col[9] = col[5]; col[5] = col[1]; col[1] = t;
t = col[2]; col[2] = col[10]; col[10] = t;
t = col[6]; col[6] = col[14]; col[14] = t;
t = col[3]; col[3] = col[7]; col[7] = col[11]; col[11] = col[15]; col[15] = t;
//同理,第4行不移位}
//定义s盒字节代换替换操作
static void SubBytes(unsigned char* col){//字节代换
int x;
for (x = 0; x < 16; x++){
col[x] = sbox[col[x]];}}
//逆向字节代换
static void Contrary_SubBytes(unsigned char* col){
int x;
for (x = 0; x < 16; x++){
col[x] = contrary_sbox[col[x]];}}
//密钥16字节--->44列32bit密钥生成--> 11组16字节:分别用于11轮轮密钥加运算
void ScheduleKey(unsigned char* inkey, unsigned char* outkey, int Nk, int Nr){
//inkey:初始16字节密钥key
//outkey:11组*16字节扩展密钥expansionkey
//Nk:4列
//Nr:10轮round
unsigned char temp[4], t;
int x, i;
/*copy the key*/
//第0组:[0-3]直接拷贝
for (i = 0; i < (4 * Nk); i++){
outkey[i] = inkey[i];}//第1-10组:[4-43]i = Nk;
while (i < (4 * (Nr + 1))) //i=4~43 WORD 32bit的首字节地址,每一个4字节
{//1次循环生成1个字节扩展密钥,4次循环生成一个WORD
//temp:4字节数组:代表一个WORD密钥
//i不是4的倍数的时候
//每个temp = 每个outkey32bit = 4字节
for (x = 0; x < 4; x++)
temp[x] = outkey[(4 * (i - 1)) + x]; //i:32bit的首字节地址
//i是4的倍数的时候
if (i % Nk == 0){/*字循环:循环左移1字节 RotWord()*/
t = temp[0]; temp[0] = temp[1]; temp[1] = temp[2]; temp[2] = temp[3]; temp[3] = t;
/*字节代换:SubWord()*/
for (x = 0; x < 4; x++){
temp[x] = sbox[temp[x]];}
/*轮常量异或:Rcon[j]*/
temp[0] ^= Rcon[(i / Nk) - 1];}
for (x = 0; x < 4; x++){
outkey[(4 * i) + x] = outkey[(4 * (i - Nk)) + x] ^ temp[x];}++i;}}
//定义轮密钥加操作
static void AddRoundKey(unsigned char* col, unsigned char* expansionkey, int round)//密匙加{ //扩展密钥:44*32bit =11*4* 4*8 = 16字节*11轮,每轮用16字节密钥
//第0轮,只进行一次轮密钥加
//第1-10轮,轮密钥加
int x;
for (x = 0; x < 16; x++){ //每1轮操作:4*32bit密钥 = 16个字节密钥
col[x] ^= expansionkey[(round << 4) + x];}}
//AES加密函数
void AesEncrypt(unsigned char* blk, unsigned char* expansionkey, int Nr){//加密区块
//输入blk原文,直接在上面修改,输出blk密文
//输入skey:
//输入Nr = 10轮
int round;
//第1轮之前:轮密钥加
AddRoundKey(blk, expansionkey, 0);
//第1-9轮:4类操作:字节代换、行移位、列混合、轮密钥加
for (round = 1; round <= (Nr - 1); round++){
SubBytes(blk); //输入16字节数组,直接在原数组上修改
ShiftRows(blk); //输入16字节数组,直接在原数组上修改
MixColumns(blk); //输入16字节数组,直接在原数组上修改
AddRoundKey(blk, expansionkey, round);}//第10轮:不进行列混合
SubBytes(blk);
ShiftRows(blk);
AddRoundKey(blk, expansionkey, Nr);}
//AES 解密函数
void Contrary_AesEncrypt(unsigned char* blk, unsigned char* expansionkey, int Nr){
int x;
AddRoundKey(blk, expansionkey, Nr);
Contrary_ShiftRows(blk);
Contrary_SubBytes(blk);
for (x = (Nr - 1); x >= 1; x--){
AddRoundKey(blk, expansionkey, x);
Contrary_MixColumns(blk);
Contrary_ShiftRows(blk);
Contrary_SubBytes(blk);}
AddRoundKey(blk, expansionkey, 0);}
};
class RSA
{
private:
// 选择两个不同的素数p和q
int p = 17;int q = 19;// 计算n
int n = p * q;//计算phi(n)
int phi = (p - 1) * (q - 1);// 选择一个与phi(n)互质的数e
int e = 7;
public:
// 求最大公约数
int gcd(int a, int b){
if (b == 0) {
return a;}else {
return gcd(b, a % b);}}
// 判断是否为素数
bool isPrime(int num) {
if (num <= 1) {
return false;}
int sqrtNum = sqrt(num);
for (int i = 2; i <= sqrtNum; i++) {
if (num % i == 0) {
return false;}} return true;}
// 求欧几里得扩展算法中的私钥d
int calculateD(int e, int phi) {
int d = 1;
while ((d * e) % phi != 1) {d++;}return d}
// 加密函数
int encrypt(int plainText, int e, int n) {
int cipherText = 1;
for (int i = 0; i < e; i++) {
cipherText = (cipherText * plainText) % n;}
return cipherText;}
int decrypt(int cipherText, int d, int n) {
int plainText = 1;
for (int i = 0; i < d; i++) {
plainText = (plainText * cipherText) % n;}
return plainText;}五、测试数据及其结果分析
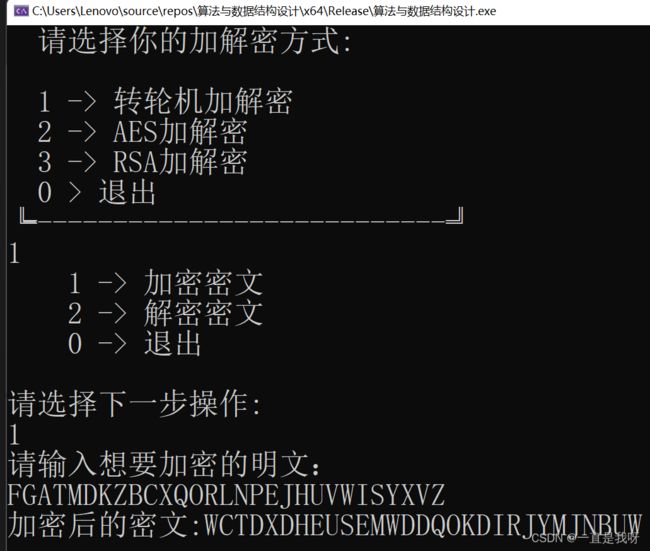
(1)我们将对文本的加密与解密系统进行测试分析,对于转轮子加解密,我们采用的明文为:“FGATMDKZBCXQORLNPEJHUVWISYXVZ”。此明文长度为30,由随机序列构成,通过如图2所示过程加密后应为“WCTDXDHEUSEMWDDQOKDIRJYMJNBUW”。之后再由转轮机解密。解密后的序列应为“FGATMDKZBCXQORLNPEJHUVWISYXVZ”。加解密测试结果如图5图6所示。
图5 转轮机加密测试图
图6 转轮机解密测试图
(2)我们将对文本的加密与解密系统进行测试分析,对于AES加密,采用16位长度明文进行加解密操作,明文为:“JEKOUVAQHVWKHQNU”,采取同等长的16位密钥进行加密,密钥采用第一步转轮机加密算法生成密钥为:“UGHLPVVMTEZTEEGE”,通过纸质计算可得,加密后的密文应该为:“03 17 7d 29 13 d6 43 55 1e 66 a4 26 12 71 bb 07”。对“03 17 7d 29 13 d6 43 55 1e 66 a4 26 12 71 bb 07”进行解密操作,应得明文为:“JEKOUVAQHVWKHQNU”。加解密测试结果如图7所示。
图7 AES算法加解密测试图
(2)我们将对文本的加密与解密系统进行测试分析,对于RSA算法加密,我们采用的是p和q两个素数,p=17,q=19(现实中p和q应为大素数)。p和q:这两个素数是RSA算法中的关键要素,用于生成公钥和私钥。n表示p和q的乘积,它是公钥和私钥的一部分。phi代表欧拉函数,用于计算与n互质的整数的个数,也是私钥的一部分。e是与phi互质的整数,被选为公钥的一部分。d是根据选定的e和phi计算出来的私钥。根据上述,n=323,phi= (p - 1) * (q - 1),e=7。我们验证时取的是23这个素数,经过加密后应该为:“82”。解密后应为:“23”。加解密测试结果如图8图9所示。
图8 RSA算法加密测试图
图9 RSA算法解密测试图
六、课题完成过程中遇到的问题及解决方法
问题1:在roatewheel函数中,轮子每次向下转动一格,但没有限制转动的范围,导致可能出现数组越界的风险,而C++语言并不会将数组越界溢出作为报错,导致代码潜在存在的风险。
解决方法:在实现轮子转动的代码中,添加检查边界的逻辑,确保转动范围不会超出数组的有效索引范围。可以使用条件语句或取模操作来限制索引的值,以保证在合法范围内进行转动。
修改代码如下:
void roatewheel(int wheel[26])
{
int temp = wheel[25];
for (int i = 24; i >= 0; i--) {
wheel[i + 1] = wheel[i]; }
wheel[0] = temp % 26; // 限制索引值在合法范围内
return; }问题2:在output数组中,字符Z被分配了一个空白字符作为替代。但是在searchindex函数中,并没有考虑空白是否为空白字符,导致程序执行到这里时会出现崩溃或者停摆错误。
解决方法:在调用searchindex函数之前,将明文字符转换为统一的大小写格式。使用std::toupper或std::tolower函数来实现,确保将明文字符和轮子中的字符都转换为相同的大小写格式,以便正确地进行索引查询和加密操作
问题3:AES算法中,roatewheel 函数轮子转动时最后一个元素的处理有误,当密文长度小于26时,加密后的密文无误,但是当密文大于26位时,由于轮子最后一个元素在处理时没有将最后一个交给第一个元素,导致轮子数据出现错误。
解决方法:将最后一个元素的处理修改为将最后一个元素的值赋给第一个元素,而不是将最后一个元素的值赋给 temp。修改后的代码如下:
void roatewheel(int wheel[26]) {
int temp = wheel[25];
for (int i = 24; i >=0; i--) {
wheel[i + 1] = wheel[i]; }
wheel[0] = temp; return;
}问题4:在output数组中,字符Z被分配了一个空白字符作为替代。但是在searchindex函数中,并没有考虑空白是否为空白字符,导致程序执行到这里时会出现崩溃或者停摆错误。
解决方法:在调用searchindex函数之前,将明文字符转换为统一的大小写格式。使用std::toupper或std::tolower函数来实现,确保将明文字符和轮子中的字符都转换为相同的大小写格式,以便正确地进行索引查询和加密操作
问题5:在给定的代码中,欧几里得扩展算法中计算私钥 d 的实现存在一个潜在的问题。之前的实现是通过递增地尝试 d 的值,直到 (d * e) % phi == 1。然而,如果给定的 e 和 phi 不满足互质的条件,即 gcd(e, phi) != 1,那么计算出的 d 值将不会是有效的私钥。这可能会导致密码系统无法正常解密。
解决方法:在计算私钥 d 之前,需要添加一个错误检查步骤来验证 e 是否与 phi 互质。如果 e 和 phi 不互质,则应该选择一个新的 e 值。具体的解决方法可以是在选择 e 时,遍历素数范围内的所有数值,找到一个与 phi 互质的值。
修改后的代码如下:
// 选择一个与phi(n)互质的数e
int chooseE(int phi) {
for (int e = 2; e < phi; e++) {
if (gcd(e, phi) == 1) {
return e; }
}
return -1; // 表示未找到合适的e值 }
// 计算d
int calculateD(int e, int phi) {
int d = 1;
while ((d * e) % phi != 1)
{ d++; }
return d; }
int main() {
int e = chooseE(phi);
if (e == -1)
{ std::cout << "Error: Unable to find a suitable value for e." << std::endl; return 0; }
}问题6:在加密和解密函数中,计算幂运算时使用了循环迭代的方式计算。然而,在加密和解密中通常涉及大数值的幂运算,循环迭代的方法效率很低。这可能会导致处理大数的加密和解密操作非常耗时。
解决方法:在处理大数值的幂运算时,可以使用模指数运算的算法,例如快速模幂运算(Exponentiation by Squaring)算法。该算法通过分解指数为二进制形式,并利用重复平方和取模操作,显著降低了计算复杂度。
修改后的代码如下:
int encrypt(int plainText, int e, int n) {
int cipherText = 1;
while (e > 0) {
if (e % 2 == 1) {
cipherText = (cipherText * plainText) % n;
}
plainText = (plainText * plainText) % n;
e /= 2;
}
return cipherText;
}
// 解密函数
int decrypt(int cipherText, int d, int n) {
int plainText = 1;
while (d > 0) {
if (d % 2 == 1) {
plainText = (plainText * cipherText) % n;
}
cipherText = (cipherText * cipherText) % n;
d /= 2;
}
return plainText;
}七、总结
这次的实验项目是一个非常有挑战性的任务,课题采用个人开发方式,我选用了C++语言进行程序设计。这个项目不仅仅是对我们在理论课程上所学知识的一个检验,更是一次深入实践、提高编程技能的机会。在这个项目中,我面临了许多具体问题,通过解决这些问题,我不断提高了程序设计和代码编写的能力。从最初的算法思考和设计,到代码的编写和调试,每一个步骤都是我们学习和成长的过程。作为计算机专业的学生,我深知学习不只是停留在书本上,更应该将知识应用于解决现实生活中的问题,这样才能锻炼我的实践能力。通过这次实验,我不仅懂得了要掌握各种数据结构和算法,还需要注重程序的功能完善和bug的修复。要不断优化程序,选择合适的数据类型,确保程序运行的高效性和稳定性。这个过程培养了我的程序设计思维,也要求我有耐心去发现和解决各个功能函数之间的联系,确保整个程序的正常运行。这个项目让我学会了灵活运用和整合已有的知识和技能,去分析和解决实际的问题。有时候我会遇到一些难以用已学知识解决的问题,这时就需要我们主动、独立学习,通过互联网、视频等渠道深入学习。例如,再上述的代码中,定义了一个布尔数组st[N] 用于标记质数和非质数。然而,在 get_primes 函数中的内层循环中,对于非质数 primes[j]*i,没有正确地标记为 true,导致后续可能错误地将其作为质数处理。这会导致最终得到错误的质数列表。解决方法是:在 get_primes 函数的内层循环中,对于非质数 primes[j]*i,应该设置对应的布尔数组st的值为 true,并且添加 break 语句来终止内层循环。这样的挑战让我意识到自己的知识和能力是可以在实践中应用和发挥的。除了个人能力的提升,这个项目还加强了我们的团队合作意识。通过合理的借鉴和讨论,我提高了效率,实现了最大化的成果。尽管这次实习只有短短两个星期,但在这段时间里,我学到了很多,收获颇丰。总的来说,这个项目是一次难得的机会,让我能够将理论知识转化为实际能力。通过解决具体问题、优化程序,我不仅提高了自己的编程技能,也增长了见识,为将来的学习和工作打下了坚实的基础。我对这次实验项目的成果感到自豪,也期待未来能继续面对更多挑战,不断提升自己。
校园导航系统
一、课题内容和要求
设计要求:根据南京邮电大学的校园平面图,设计校园导航系统。以图中顶点表示校内各地点(图书馆、教学楼、行政楼、食堂、宿舍等)的位置,存放具体地点名称、简介等信息;以边表示路径,存放路径长度等相关信息。要求完成下述的系统功能:
(1)为来访客人提供图中任意景点的问路查询,即查询任意两个景点之间的一条最短的路径。
(2)以图形化界面形式输出路径。
二、课题需求分析
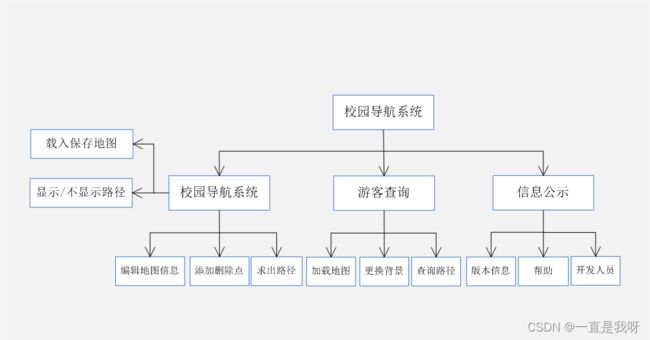
课题目标“校园导航系统”的功能框架图如图10所示
图10 功能框架图
(1)对游客提供详细的地图呈现和地图服务;
(2)提供选择地图的多种选择;
(3)对于管理人员提供地图管理服务;
(4)界面输出并以图形化界面形式输出路径。
三、课题相关数据结构及算法设计
1 主要数据结构
QPoint P1, P2; //两个临时点,用于
QPoint P[51]; //最大点数组,防止越界
QString Pl[51], pic;
//每个点的标签,pic为当前背景图片的存储路径,将点显示于背景之上
int ways; //右侧显示栏路径的数量
double dis, min; //dis是搜索路径时路径长度当前值,min是路径长度最小值
bool showlen = false; //是否显示当前路径长度
bool showlen_1=false; //是否显示当前路径
struct lines { int a, b; bool f = false; } temp1, line[101]; //两点之间的连线,ab是两点p1,p2的下标,f是否是最短路径,如是则标红,否则保持蓝色。temp1是当前线,line数组存储所有线
class Stack //用于dfs,遍历时,“错误”路径时倒退
{
private:
int a[51] = {};//存储点的下标,最大为51个
int num = 0;//初始化点的个数
public:
void push(int n) { a[++num] = n; } //将数据压入栈
void pop() { a[num--] = 0; } //数据出栈
QString getstr() //获取查询结果信息,在右侧显示栏中的标签显示路径结果
{QString str = "";
for (int i = 1; i < num; i++)
str += Pl[a[i]] + "->"; //不同路径之间用"->"隔开
str += Pl[a[num]];
return str;}2 主要算法流程
考虑到现实生活中,如果游客想要访问游玩一个从没有去过的景点或地方,通常采用从入口进入然后一直走下去的方式,这在图论中符合深度优先遍历图的特点,而且考虑到深度优先算法对时间复杂度和空间复杂度对于本系统而言均较合适,在做成系统时能够更快速的查找输出,所以在本课题中,查找算法采用深度优先遍历算法(Depth-First Algorithm)。
深度优先算法的遍历策略为:访问第一个邻接结点:从起始点出发,该起始点可能有若干邻接结点,访问第一个邻接结点,然后再访问第一个邻接结点的第一个邻接结点,每次都访问当前结点的第一个邻接结点;优先向纵向遍历,不是对当前结点的所有邻接结点进行横向遍历。递归过程:上述 DFS,每次访问起始点的第一个邻接结点后,又将该第一个邻接结点作为新的起始点继续向下访问,该过程是一个递归过程。
以在下面的无权图中找到从节点a到节点i的路径为例,说明一下DFS算法的工作流程,如图11所示:
图11 DFS例图
按照上节的图搜索算法的基本流程进行搜索,过程如图12所示:
图12 DFS搜索流程图
从i回溯得到路径:a->b->c->g->i,如图13所示:
DFS能够快速地找到一条路径,是一种以时间换空间的方法。我们常将其应用到二维地图的路径规划中。
四、源程序代码
#include "window2_1.h"
#include "ui_window2_1.h"
#include
#include
#include
#include
#include
#include
QPoint P1, P2; //两个临时点,用于
QPoint P[51]; //最大点数组,防止越界
QString Pl[51], pic; //每个点的标签,pic为当前背景图片的存储路径,将点显示于背景之上
int ways; //右侧显示栏路径的数量
double dis, min; //dis是搜索路径时路径长度当前值,min是路径长度最小值
bool showlen = false; //是否显示当前路径长度
bool showlen_1=false; //是否显示当前路径
struct lines { int a, b; bool f = false; } temp1, line[101];
//两点之间的连线,ab是两点p1,p2的下标,f是否是最短路径,如是则标红,否则保持蓝色。temp1是当前线,line数组存储所有线
class Stack //用于dfs,遍历时,“错误”路径时倒退
{
private:
int a[51] = {}; //存储点的下标,最大为51个
int num = 0;//初始化点的个数
public:
void push(int n) { a[++num] = n; } //将数据压入栈
void pop() { a[num--] = 0; } //数据出栈
QString getstr() //获取查询结果信息,在右侧显示栏中的标签显示路径结果
{ QString str = "";
for (int i = 1; i < num; i++)
str += Pl[a[i]] + "->"; //不同路径之间用"->"隔开
str += Pl[a[num]];
return str;}
void showline()//将最短路径标红{
for (int i = 1; i < num; i++)
{
for (int j = 1; line[j].a && j <= 100; j++) //在line[j]存在并且line数量在100以内循环
if ((line[j].a == a[i] && line[j].b == a[i + 1]) || (line[j].b == a[i] && line[j].a == a[i + 1]))//如果线当中点的下标与最短路径栈中存储的点下标相同
{
line[j].f = true; //将最短路径标红
break;
}
}
}
}stack, temp2; //temp2存储最短路径对应的栈
int count = 0; //添加的点的默认下标
double window2_1::dist(QPoint a, QPoint b) //计算两点间距离,将结果返回给dist
{
return sqrt((a.x() - b.x()) * (a.x() - b.x()) + (a.y() - b.y()) * (a.y() - b.y()));
}
bool window2_1::isin(QPoint x, QPoint y, int n)//判断鼠标光标是否点击成功(半径n的圆域范围内)
{
if (dist(x, y) <= n) return true;
else return false;
}
window2_1::window2_1(QWidget* parent) : //构造函数
QMainWindow(parent),
ui(new Ui::window2_1)
{
ui->setupUi(this);
this->resize(1500,1000); //约定窗口大小
using namespace std;
QString filename = "E:/QtCode/CampusNavigationMap/MapResource.map2"; //在界面打开时就加载地图
if (filename != "")
{
ifstream in(filename.toStdString());
if (in.is_open()) //如果打开则进行读取操作
{
string c;
in >> c;
ui->label_6->setText(QString::fromStdString(c));//转变为Qstring
in >> num1 >> num2;
for (int i = 1; i <= num2; i++)
{
int a, b;
in >> a >> b;
P[i].setX(a);
P[i].setY(b);
in >> c;
Pl[i] = QString::fromStdString(c);
}
for (int i = 1; i <= num2; i++)
for (int j = 1; j <= num2; j++)
in >> matrix[i][j];
for (int i = 1; i <= num1; i++)
in >> line[i].a >> line[i].b;
in >> c;
pic = QString::fromStdString(c);
clr();
in.close();//关闭文件
}
else QMessageBox::information(this, "提示", "读取失败"); //反之则报错
}
}
window2_1::~window2_1() //析构函数
{
delete ui;
}
void window2_1::DFS(int i, int j) //i为点的起点,j为点的终点
{
reach[i] = true; //起点到达
stack.push(i); //将起点压入栈内
if (i == j)//判断已经到达终点
{
if (ways <= 200000) ui->listWidget->addItem(stack.getstr() + ",长度为:" + QString::number(dis)), ways++;
if (min == 0 || dis < min)//将最短路径值赋给min以及temp2
{
min = dis;
temp2 = stack;
}
}
else//未到达终点,遍历所有可行途径
for (int t = 1; t <= num2; t++)
if (matrix[i][t] && !reach[t])//matrix[i][t]存在,即该路径存在,并且P[t]未达到
{
dis += matrix[i][t];//当前路径长度+目前点到下一个点的距离
DFS(t, j);//递归,t为新的起点
dis -= matrix[i][t];//更换新路径,将此前路径长度减去
}
stack.pop();//将最新的点弹出
reach[i] = false;//因为此点弹出,故未达到
}
void window2_1::clr()//清除右侧显示栏的显示信息
{
ui->label_4->setText("");
ui->label_5->setText("");
ui->listWidget->clear();
ui->listWidget_2->clear();
for (int i = 1; i <= num1; i++)
if (line[i].f) line[i].f = false; //红线变回蓝线
update();//调用paintEvent函数
}
void window2_1::paintEvent(QPaintEvent*) //绘图函数
{
QPainter painter(this);//画笔,this为当前窗口
painter.drawPixmap(450,50,380,536, QPixmap(pic));//载入背景图片并显示出来
QFont font1("Microsoft YaHei", 9);//字体说明
QFont font2("Microsoft YaHei", 12);
painter.drawRect(450,50,380,536);//矩形大小,窗口大小
painter.setFont(font1);
painter.setRenderHint(QPainter::Antialiasing, true);//使接下来的绘图光滑
if (showlen_1)//如果显示路径
for (int i = 1; i < num2; i++)
for (int j = i + 1; j <= num2; j++)
if (matrix[i][j])//若路径存在
{for (int i = 1; i <= num1; i++)
{if (!line[i].f) painter.setPen(Qt::blue);//设置画笔颜色为蓝色
else painter.setPen(Qt::red);
painter.drawLine(P[line[i].a], P[line[i].b]);//两点连线}}
painter.setPen(Qt::darkMagenta);
if (showlen)//如果显示路径长
for (int i = 1; i < num2; i++)
for (int j = i + 1; j <= num2; j++)
if (matrix[i][j])//若路径存在{
int x1, y1;
x1 = (P[i].x() + P[j].x()) / 2 - 10;//路径中央偏左
y1 = (P[i].y() + P[j].y()) / 2 + 4;//路径中央偏下
painter.drawText(QPoint(x1, y1), QString::number(matrix[i][j]));
//路径长度显示在(x,y)位置处}
painter.setPen(Qt::black);
painter.setBrush(Qt::yellow);
painter.setFont(font2);
for (int i = 1; i <= num2; i++)
{
painter.drawEllipse(P[i], 4, 4); //把点画出来
painter.drawText(QPoint(P[i].x() + 5, P[i].y() + 6), Pl[i]);//画出点的标签,pl[i]为标签
}
ui->label_2->setText("点数:" + QString::number(num2));
ui->label_3->setText("路径数:" + QString::number(num1));
}
void window2_1::mousePressEvent(QMouseEvent* event)//功能实现
{
if (event->button() == Qt::LeftButton)
{
QPoint temp = event->pos();//event->pos为当前点击位置
switch (tp)
{
case 1://选择第一个点
if (num1 == 100) QMessageBox::warning(this, "警告", "路径数已达上限");
else
for (int i = 1; i <= num2; i++)
if (isin(temp, P[i]))//选中
{
P1 = P[i]; line[num1 + 1].a = i; tp = 2; ui->label->setText("请选择第二个点"); break;//将第一个点信息存入P1,line[num1+1],并开始case2功能
}
break;
case 2://选择第二个点
for (int i = 1; i <= num2; i++)
if (P[i] != P1 && isin(temp, P[i]))//若选中了与第一个点不同的点
{
int t = num1++;//线数量+1
P2 = P[i]; line[num1].b = i; tp = 1;
//P2信息录入,完善line[num1]信息(num1已+1),tp回归1.
if (line[num1].a > line[num1].b) //保证线的第一个点下标比第二个小
{
int t1 = line[num1].a; line[num1].a = line[num1].b; line[num1].b = t1;
}
for (int j = 1; j < num1; j++) //判断是否路线已经存在
{
if (line[num1].a == line[j].a && line[num1].b == line[j].b)
{
line[num1--] = line[0];
QMessageBox::warning(this, "警告", "两条路径重合");
break;
}
}
if (t != num1)//将两点间的像素距离赋值给两点间的路径长度(默认)
matrix[line[num1].a][line[num1].b] = matrix[line[num1].b][line[num1].a] = dist(P[line[num1].a], P[line[num1].b]);
ui->label->setText("请选择第一个点");
break;
}
update();
break;
case 3://添加点
if (num2 < 50 && temp.x() >= 450 && temp.x() <=830 && temp.y()>50 && temp.y() <= 586)//判断所加的点是否在窗口范围内
{
int t = num2++;
for (int i = 1; i < num2; i++)
if (isin(temp, P[i], 20))
//判断两点是否太近,选中条件为“半径10的圆邻域”,故两点距离需要大于20
{num2--; QMessageBox::warning(this, "警告", "两个点靠太近");}
if (t == num2) break;
P[num2] = event->pos();//当前位置赋给最新的P点
Pl[num2] = QString::number(++count);//创建默认标签
update();
}
else if (num2 == 50) QMessageBox::warning(this, "警告", "点数已达上限");
else QMessageBox::warning(this, "警告", "点超出边界");
break;
case 4://删除点
if (num2 == 0) QMessageBox::warning(this, "警告", "无任何点");
else
for (int i = 1; i <= num2; i++)
if (isin(temp, P[i]))//选中想要删除的点
{
for (int j = i; j < num2; j++)
{
P[j] = P[j + 1];//将删除的点后的点前移
Pl[j] = Pl[j + 1];//点的标签同理
for (int k = 1; k <= num2; k++)
//此一系列对matrix的操作使该点下标对应的行列删除
matrix[j][k] = matrix[j + 1][k];}
for (int j = i; j < num2; j++)
for (int k = 1; k <= num2; k++)
matrix[k][j] = matrix[k][j + 1];
for (int j = 1; j <= num2; j++)
matrix[j][num2] = matrix[num2][j] = 0;
Pl[num2] = Pl[0];//最后一个点标签消失
P[num2--] = P[0];//最后一个点消失
for (int j = 1; j <= num1; j++)
{if (i == line[j].a || i == line[j].b)//将line数组一并前移
{for (int k = j; k < num1; k++)
line[k] = line[k + 1];
line[num1--] = line[0];//将最后一条线消除,同时线数量减一
j--;}
else//下标原在被选中的点之后的点所在线的下标前移
{if (line[j].a > i) line[j].a--;
if (line[j].b > i) line[j].b--;}}
update();
break;
}
break;
case 5://选择第一个点删除路径
if (num1 == 0) QMessageBox::warning(this, "警告", "无任何路径");
else
for (int i = 1; i <= num2; i++)
if (isin(temp, P[i]))//判断选中
{
P1 = P[i]; temp1.a = i; tp = 6; ui->label->setText("请选择要删除路径的第二个点");
}
break;
case 6://选择第二个点删除路径
for (int i = 1; i <= num2; i++)
{
if (P[i] != P1 && isin(temp, P[i]))//选中
{
P2 = P[i]; temp1.b = i; tp = 5;//第二个点信息载入
if (temp1.a > temp1.b)//保证线的第二个点下标大于第一个
{
int t1 = temp1.a; temp1.a = temp1.b; temp1.b = t1;
}
int t3 = num1;
for (int j = 1; j <= num1; j++)
{
if (temp1.a == line[j].a && temp1.b == line[j].b)
{
matrix[line[j].a][line[j].b] = matrix[line[j].b][line[j].a] = 0;//点之间路径长度删除
{for (int k = j; k < num1; k++)
line[k] = line[k + 1];//路径(线)下标前移
line[num1--] = line[0];
break; }
}
}
ui->label->setText("请选择要删除路径的第一个点");
if (num1 == t3) QMessageBox::warning(this, "警告", "找不到这条路径");
else break;}}
update(); break;
case 7://编辑点的标签
if (num2 == 0) QMessageBox::warning(this, "警告", "无任何点");
else
for (int i = 1; i <= num2; i++)
if (isin(temp, P[i]))
{
QString s0 = QInputDialog::getText(this, "编辑标签", "输入文本(最多13个字)");
if (s0 != "") Pl[i] = s0.left(13);
break;}
break;
case 8://选择起点
for (int i = 1; i <= num2; i++)
if (isin(temp, P[i]))
{P1 = P[i]; tp = 9; ui->label->setText("请选择终点");
temp1.a = i;//起点下标赋给temp1
ui->label_4->setText("起点:" + Pl[i]);
ui->label_5->setText("终点:");
break;}
break;
case 9://选择终点
for (int i = 1; i <= num2; i++)
if (P[i] != P1 && isin(temp, P[i]))//判断不与起点重合
{ P2 = P[i];
temp1.b = i;//终点下标赋给temp1
ui->label_5->setText("终点:" + Pl[i]);
ui->listWidget->clear();
ways = 0;
min = 0;
DFS(temp1.a, temp1.b);
if (ways)//若有路
{
if (ways > 200000) ui->listWidget->addItem("路径数过多,超过200000条,无法完全显示!最短路径为:" + temp2.getstr() + ",长度为:\n\n" + QString::number(min));
else ui->listWidget_2->addItem("共" + QString::number(ways) + "条路径,其中最短路径为:" + temp2.getstr() + ",长度为:" + QString::number(min));
temp2.showline(); //最短路径展示
update();
}
else ui->listWidget->addItem("找不到路径");
tp = 0;
ui->label->setText(""); break;
}
break;
case 10://编辑路径长度第一个点
if (num1 == 0) QMessageBox::warning(this, "警告", "无任何路径");
else
for (int i = 1; i <= num2; i++)
if (isin(temp, P[i]))//选中
{
P1 = P[i]; tp = 11; ui->label->setText("请选择要编辑路径长度的第二个点");//转入下一个case
temp1.a = i;
break;
}
break;
case 11://编辑路径长度第二个点
for (int i = 1; i <= num2; i++)
if (P[i] != P1 && isin(temp, P[i]))//不与第一个点重合
{
P2 = P[i];
temp1.b = i;
tp = 10;
if (temp1.a > temp1.b)//保证线的第二个点下标大于第一个
{
int t1 = temp1.a; temp1.a = temp1.b; temp1.b = t1;
}
bool f0 = false;
for (int j = 1; j <= num1; j++)
{
if (temp1.a == line[j].a && temp1.b == line[j].b)
{
double number = QInputDialog::getDouble(this, "编辑长度", "输入浮点数(0.0001~999999)", matrix[temp1.a][temp1.b], 0.0001, 999999, 4);
if (number) matrix[temp1.a][temp1.b] = matrix[temp1.b][temp1.a] = number;//若输入了数,则点之间长度更改
f0 = true;
break;
}
}
ui->label->setText("请选择要编辑路径长度的第一个点");
if (!f0) QMessageBox::warning(this, "警告", "找不到这条路径");
update();
break;
}
break;
}
}} 五、测试数据及其结果分析
我将对校园导航系统进行测试与分析。
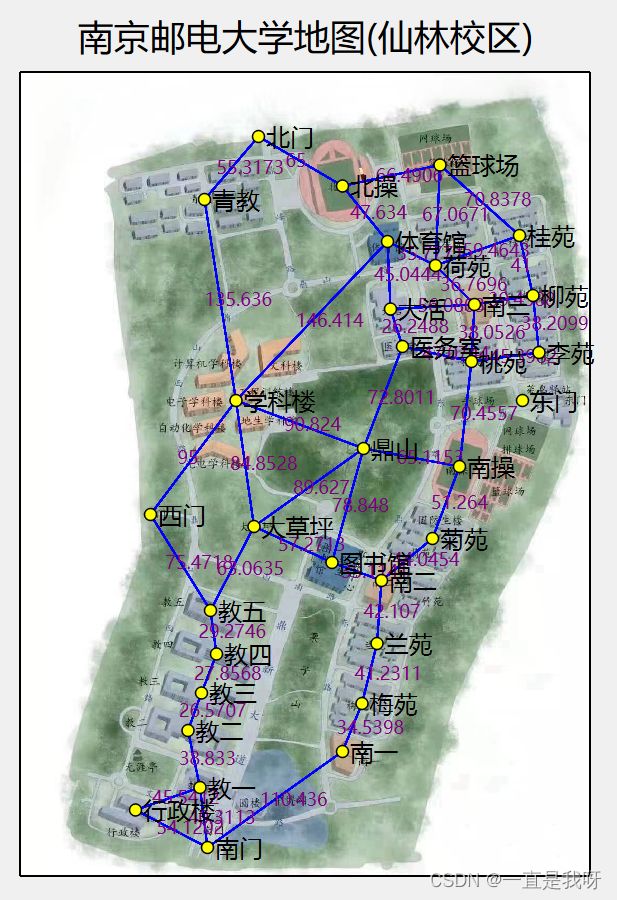
此次测试采用由南京邮电大学官方手绘地图作为模板绘制,具体地图如图14所示,我们在上面标注了“北操、青教、篮球场、体育馆、大活、医务室”等标志性地点,并根据实际道路连接情况进行了路径连接,保存好的地图命名为MapResource.map2。连接好的测试地图如图15所示。
图14 校园地图
图15 绘制完成地图
测试时,我们选取图书馆到青教作为出发点和终点,通过路径信息可知,两地最短路径为:图书馆->大草坪->学科楼->青教。测试结果如图16所示
图16 功能测试图
通过测试结果可知,由于采用DFS深度优先算法,当出现较多点时,可能的路径也会呈现较快增长,观察窗口可知,最短路径为:“图书馆->大草坪->学科楼->青教”,与预期结果相同。
六、课题完成过程中遇到的问题及解决方法
问题1:在切换MainWindow与AdminWindow时出现切换失效和切换崩溃的问题。
解决方法:这是由于最初写代码没有释放上一个界面的内存,最初的写法造成内存的浪费和不必要的申请。解决方法是在主窗口中增加副窗口的头文件(副窗口为从主窗口打开或切换的窗口),并在主窗口头文件中为副窗口申请一个空窗口(不要在头文件中直接定义,否则可能造成内存泄漏问题),之后在主窗口中申请对象,这样的话在主窗口关闭时,其析构函数也会将副窗口一并析构,从而释放内存。
问题2:由于地图文件是由管理员写入,其文件地址定义在管理员的保存地址,导致在QT在打包发送后,用户在没有更改的情况下,地图资源并不能及时加载。
解决方法:在用户使用界面中增加了加载地图和更换背景功能,让用户自己选择不同的地图的同时,及时加载地图信息。
问题3:在管理员登陆时,输入正确密码后,会先弹出用户名/密码信息错误后登入。
解决方法:由于管理员登陆按钮拥有两个功能:(1)检测管理员输入用户名密码信息是否正确。(2)跳转到地图管理界面。在执行时,按钮按照上述功能执行,导致在正确输入密码后仍会弹出错误信息弹窗,解决方法为:Qt的PushButton的常用的三种响应有pressed,released和clicked。优先级:pressed>released>clicked。按下按钮pressed函数的内容,释放按钮先执行released函数的内容,再执行clicked函数的内容。所以我们将检测信息是否正确的点击事件换成pressed或released即可。
问题4:在管理员绘制地图时,添加的点并没有位置限制,导致可以在地图框外添加点。
解决方法:添加添加点的限制逻辑,通过判断鼠标点击位置为半径的一个圆是否与地图接壤,如果接壤说明点合法,在地图内。具体代码如下:
double window2_1::dist(QPoint a, QPoint b) //计算两点间距离,将结果返回给dist
{
return sqrt((a.x() - b.x()) * (a.x() - b.x()) + (a.y() - b.y()) * (a.y() - b.y()));
}
bool window2_1::isin(QPoint x, QPoint y, int n)
七、总结
在这次实践周中,我有幸选择了开发校园导航系统。这是一次非常宝贵的经历,通过这个项目,我收获了许多知识和经验,同时也深刻地体会到了软件开发的挑战与乐趣。我的校园导航系统旨在为学生和访客提供一个方便快捷的导航工具,帮助他们查找和定位校园内的各种地点。系统具备地图展示、搜索功能以及路径规划等核心功能,通过QT的图形界面编程实现。在开发过程中,我面临了许多技术挑战。首先,地图展示是一个重点难点,需要借助QT的图形库绘制校园地图,并实现用户的交互操作。其次,路径规划算法的选择和实现也是一个复杂的任务,需要兼顾效率和准确性。此外,系统的稳定性和用户友好性也是我需要关注的问题。学习和成长在解决这些挑战的过程中,我深刻地学到了很多东西。我学会了如何使用QT库进行图形界面设计和编程,掌握了绘制地图、处理用户输入、展示数据等技巧。我还研究了不同的路径规划算法,并进行了性能测试和比较,提高了自己的算法设计思维。在错误和问题中,我不断调试和改进代码,积累了丰富的调试经验。这次校园导航系统的开发经历让我深受启发。我意识到软件开发是一个不断学习和成长的过程,每一个挑战都蕴含着新的机遇和发展。同时,我也认识到了理论知识和实践经验的重要性,只有不断探索和实践,才能真正提升自己的能力和水平。我希望能够继续深耕软件开发领域,并不断学习新的技术和工具。我将这次经历视为我成长道路上的一个重要里程碑,为未来的学习和职业发展打下了坚实的基础。我将继续保持学习的热情和探索的精神,迎接更多的挑战和机遇。"成功的关键在于始终保持学习的态度和勇于尝试的精神" 。