C语言数据结构之线性表-栈和队列篇
心中若有桃花源
何处不是水云间
烟雨长虹,孤鹜齐飞的个人主页
个人专栏
前期回顾-双向链表
期待小伙伴们的支持与关注!!!
目录
栈
栈的概念及结构
栈的概念#
栈的核心操作#
栈的实现
栈的声明
栈的创建
栈的销毁
入栈
出栈
获取栈顶元素
获取栈中有效元素个数
检测栈是否为空
代码测试
代码的整体实现
队列
队列的概念及结构
队列的概念#
队列的核心操作#
队列的实现
队列的声明
队列的创建
队列的销毁
入队列
出队列
获取队列头部元素
获取队列尾部元素
获取队列中有效元素个数
检测队列是否为空
代码的测试
代码的整体实现
总结 :
栈
栈的概念及结构
栈的概念#
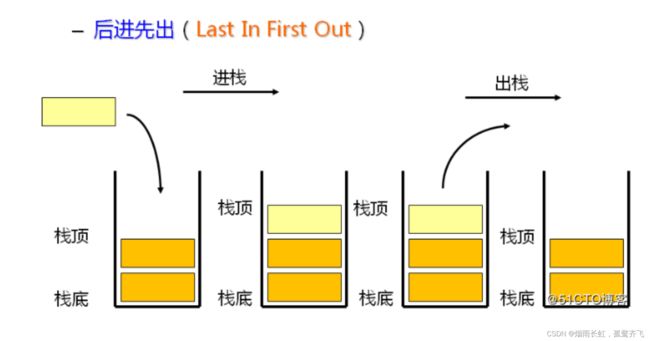
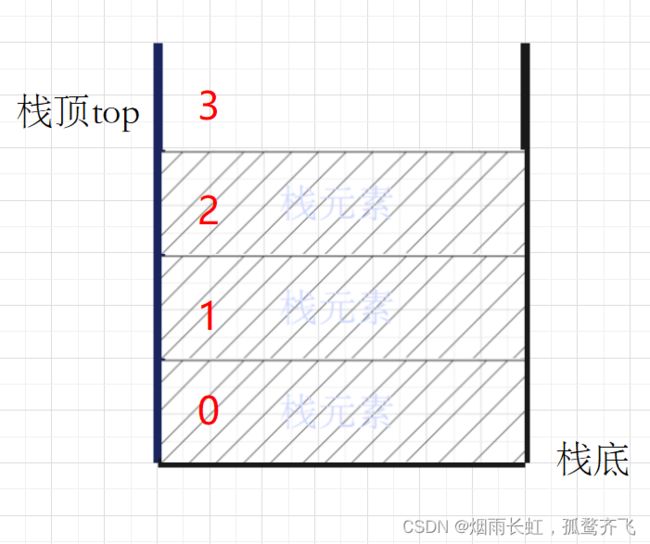
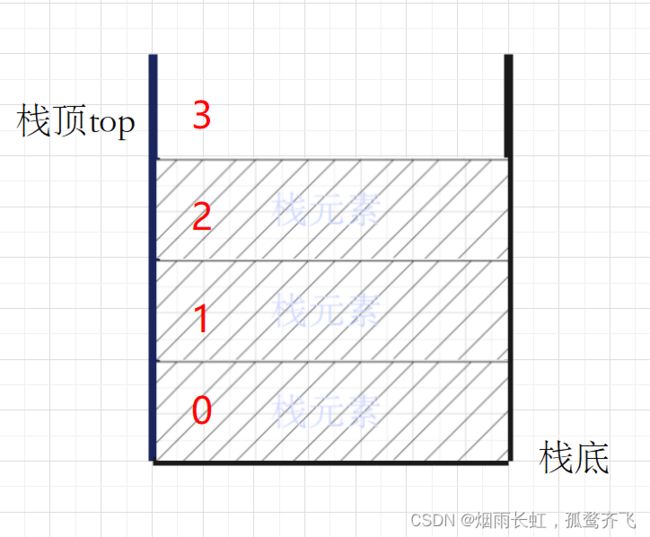
一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。 进行数据插入和删除操作的一端 称为栈顶,另一端称为栈底。 栈中的数据元素遵守 后进先出 LIFO ( Last In First Out)的原则(栈的运用就比如我们在用浏览器浏览东西时,不管什么浏览器都会有一个 返回键,点击后会按照你访问的顺序逆序后退 )栈的核心操作#
三大核心操作, 压栈 , 出栈 , 取栈顶元素压栈:栈的插入操作叫做压栈(进栈或入栈), 入数据在栈顶出栈:栈的删除操作叫做出栈, 出数据也在栈顶(压栈就如一颗颗子弹被压入弹夹,出栈就如被弹出的子弹壳,是一种 后进先出 的状态)
栈的实现
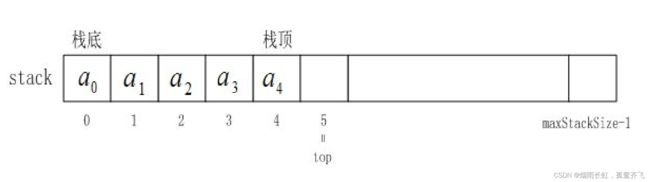
栈的实现一般可以使用 数组或者链表实现 ,相对而言数组的结构实现更优一些因为数组在尾上插入数据和删除数据的代价比较小以下我们以 顺序表 的形式实现栈我们 入栈用尾插 来实现、 出栈用尾删 来实现、 取栈顶元素就是取尾部元素注意:我们在用顺序表来实现栈的时候选取的是在 顺序表的尾部 来进行的,但这并不是说在顺序表的头部就不能实现。只是在头部实现的时候,不管是头插还是头删都要进行元素的搬运,时间复杂度太高,所以不选取
栈的声明
这里定义了一个顺序动态存储的栈,它包含了三个元素:data,top,capacity其中:
data 是指向栈底的指针变量
top 是指向栈顶的指针变量
capacity 指示栈的当前可使用的最大容量
typedef int StackDataType; //类型的重命名,防止以后修改类型带来的麻烦 typedef struct Stack //栈的结构体声明 { StackDataType* data; //入栈的元素 int top; //栈顶 int capacity; //栈可用的最大容量 }STK;
栈的创建
void StackInit(STK* ps) { assert(ps); //判断栈为不为空 ps->data = (StackDataType*)malloc(sizeof(StackDataType)*4);//动态开辟空间 if (ps->data == NULL) //判断空间是否开辟成功 { perror("malloc"); exit(-1); } ps->capacity = 4; //存储空间 ps->top = 0; //还没有元素入栈时栈顶为0 }
栈的销毁
销毁一个栈是要 释放该栈所占据的物理内存空间
void StackDestory(STK* ps) { assert(ps); //判断栈是否为空 free(ps->data); //释放空间 ps->data = NULL; ps->top = ps->capacity = 0; //栈顶和容量都归零 }
入栈
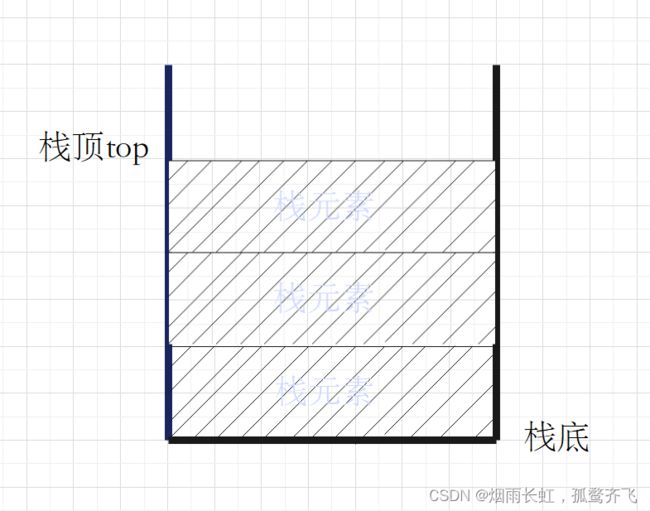
入栈操作要在栈顶进行,每次向栈中压入一个数据,top指针就要+1,直到栈满为止
void StackPush(STK* ps,StackDataType x) { assert(ps); //判断栈是否为空 if (ps->top == ps->capacity) //判断栈的空间是否够用,不够则扩容 { //扩容二倍 StackDataType* newNode = (StackDataType*)realloc(ps->data, ps->capacity * 2 * sizeof(StackDataType)); if (newNode == NULL) { perror("realloc"); exit(-1); } else { ps->data = newNode; ps->capacity *= 2; } } ps->data[ps->top] = x; //入栈元素 ps->top++; //栈顶的位置加一 }
出栈
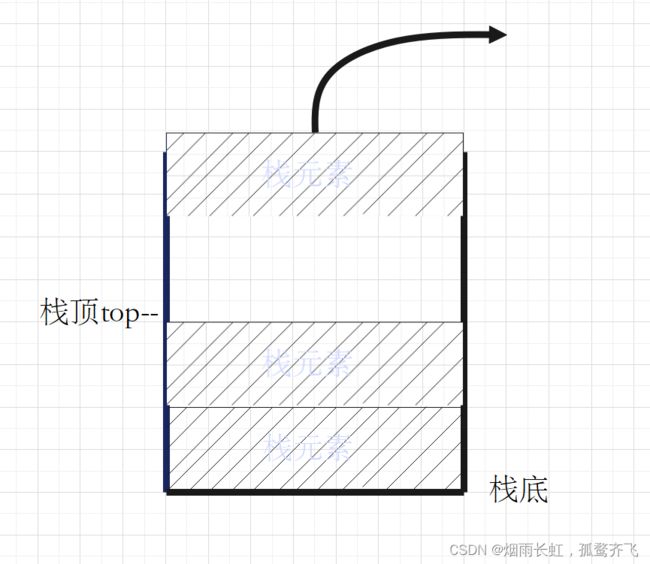
出栈(pop)操作:是在栈不为空的情况下(注意一定要进行判空操作),将栈顶的元素删除,即ps->top--
void StackPop(STK* ps) { assert(ps); //判断栈是否为空 assert(ps->top > 0); //判断栈内元素是否为空 ps->top--; //出栈 }
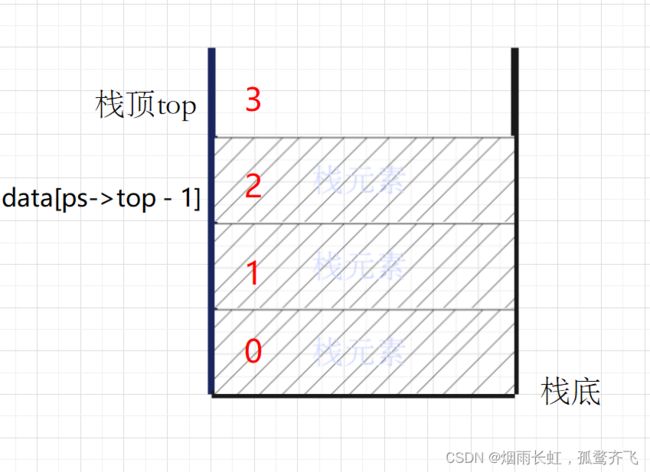
获取栈顶元素
StackDataType* StackTop(STK* ps) { assert(ps); //判断栈是否为空 assert(ps->top > 0); //判断栈内的元素是否为空 return ps->data[ps->top - 1];// 获取栈顶元素 }
获取栈中有效元素个数
int StackSize(STK* ps) { assert(ps); //判断栈是否为空 return ps->top; //栈顶的高度即为有效元素个数 }
检测栈是否为空
bool StackEmpty(STK* ps) { assert(ps); //判断栈是否为空 return ps->top == 0;//如果为空返回非零结果,如果不为空返回0 }
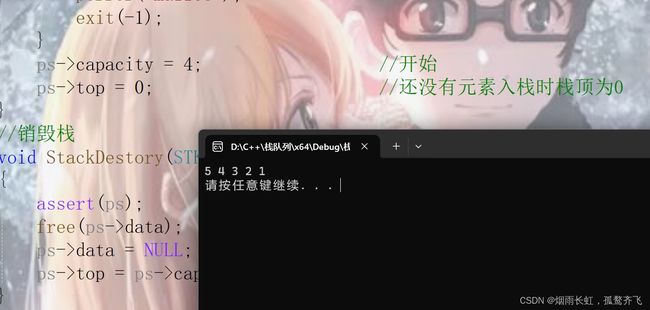
代码测试
void TestStack() { STK st; StackInit(&st); //栈的初始化 StackPush(&st, 1); //入栈 StackPush(&st, 2); StackPush(&st, 3); StackPush(&st, 4); StackPush(&st, 5); while (!StackEmpty(&st)) //循环遍历栈,直到栈内元素为空 { printf("%d ", StackTop(&st));//获取栈顶元素 StackPop(&st); //弹出栈顶元素 } printf("\n"); StackDestory(&st); //销毁栈 } int main() { TestStack(); system("pause"); return 0; }
代码的整体实现
#include#include #include #include typedef int StackDataType; typedef struct Stack { StackDataType* data; int top; int capacity; }STK; void StackInit(STK* ps) { assert(ps); ps->data = (StackDataType*)malloc(sizeof(StackDataType)*4); if (ps->data == NULL) { perror("malloc"); exit(-1); } ps->capacity = 4; ps->top = 0; } void StackDestory(STK* ps) { assert(ps); free(ps->data); ps->data = NULL; ps->top = ps->capacity = 0; } void StackPush(STK* ps,StackDataType x) { assert(ps); if (ps->top == ps->capacity) { StackDataType* newNode = (StackDataType*)realloc(ps->data, ps->capacity * 2 * sizeof(StackDataType)); if (newNode == NULL) { perror("realloc"); exit(-1); } else { ps->data = newNode; ps->capacity *= 2; } } ps->data[ps->top] = x; ps->top++; } void StackPop(STK* ps) { assert(ps); assert(ps->top > 0); ps->top--; } StackDataType* StackTop(STK* ps) { assert(ps); assert(ps->top > 0); return ps->data[ps->top - 1]; } int StackSize(STK* ps) { assert(ps); return ps->top; } bool StackEmpty(STK* ps) { assert(ps); return ps->top == 0; } void TestStack() { STK st; StackInit(&st); StackPush(&st, 1); StackPush(&st, 2); StackPush(&st, 3); StackPush(&st, 4); StackPush(&st, 5); while (!StackEmpty(&st)) { printf("%d ", StackTop(&st)); StackPop(&st); } printf("\n"); StackDestory(&st); } int main() { TestStack(); system("pause"); return 0; }
队列
队列的概念及结构
队列的概念#
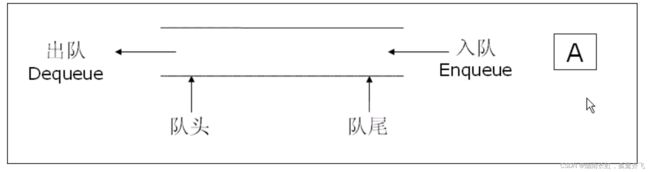
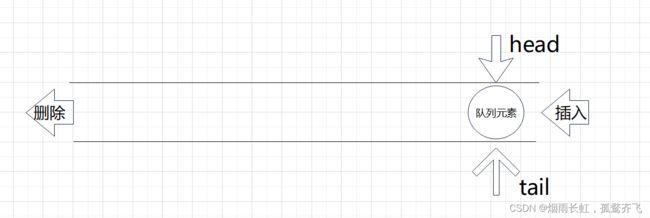
只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有 先进先出 FIFO(First In First Out)的原则(队列的运用就比如在医院挂号看诊,先取号的病患先看诊,是一种 先进先出 的状态)队列的核心操作#
入队列、 出队列入队列:进行插入操作的一端称为队尾出队列:进行删除操作的一端称为 队头
队列的实现
队列也可以数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数组头上出数据,效率会比较低以下是以 单链表 的形式实现队列我们 入队列 可以用 尾插 实现, 出队列 可以用 头删 来实现
队列的声明
typedef int QDataType; //类型的重命名,防止以后修改类型带来的麻烦 //链式结构:表示队列 typedef struct QueueNode { struct QueueNode* next; QDataType data; }QNode; //队列的结构:创建两个指针(命名为 head 和 tail)分别指向链表中队列的队头元素和队尾元素 typedef struct Queue { QNode* head; QNode* tail; }Queue;
队列的创建
void QueueInit(Queue* pq) { assert(pq); //判断队列是否为空 pq->head = pq->tail = NULL; }
队列的销毁
void QueueDestory(Queue* pq) { assert(pq); //判断队列是否为空 QNode* cur = pq->head; //定义一个指针指向队列的头节点 while (cur) //循环遍历释放空间 { QNode* next = cur->next; free(cur); cur = next; } pq->head = pq->tail = NULL; }
入队列
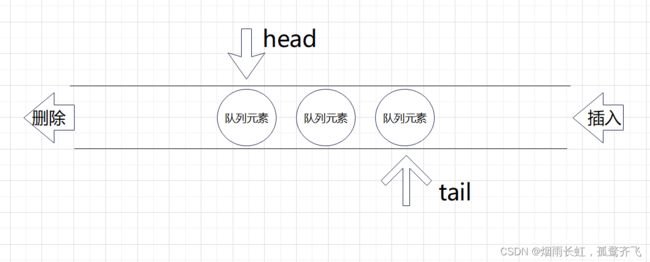
入队列:队尾入(尾插)
void QueuePush(Queue* pq, QDataType x) { assert(pq); //判断队列是否为空 QNode* newNode = (QNode*)malloc(sizeof(QNode)); //开辟动态空间 if (newNode == NULL) //判断空间是否开辟成功 { perror("malloc"); exit(-1); } newNode->data = x; //导入队列数据 newNode->next = NULL; if (pq->tail == NULL) //判断队列元素是否为空 { pq->head = pq->tail = newNode; //如果为空就头尾指针指向新开辟的空间 } else //如果不为空就进行尾插 { pq->tail->next = newNode; pq->tail = newNode; } }
出队列
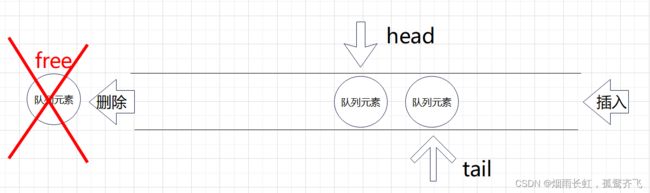
出队列:队头出(头删)
void QueuePop(Queue* pq) { assert(pq); //判断队列是否为空 assert(pq->head); //判断队列元素是否为空 if (pq->head->next == NULL)//如果队头的后继节点为空 { free(pq->head); //直接释放当前节点 pq->head = pq->tail = NULL; } else //如果对头的后继节点不为空,就进行头删 { QNode* next = pq->head->next; free(pq->head); pq->head = next; } }
获取队列头部元素
QDataType QueueFornt(Queue* pq) { assert(pq); //判断队列是否为空 assert(pq->head); //判断队列元素是否为空 return pq->head->data; //获取队列头部元素 }
获取队列尾部元素
QDataType QueueBack(Queue* pq) { assert(pq); //判断队列是否为空 assert(pq->head); //判断队列元素是否为空 return pq->tail->data; //获取队列队尾元素 }
获取队列中有效元素个数
int QueueaSize(Queue* pq) { assert(pq); //判断队列是否为空 int size = 0; //记录元素变量 QNode* cur = pq->head; //循环遍历链表记录元素个数 while (cur) { ++size; cur = cur->next; } return size; }
检测队列是否为空
bool QueueEmpty(Queue* pq) { assert(pq); //判断队列是否为空 return pq->head == NULL; //如果为空返回非零结果,如果非空返回NULL }
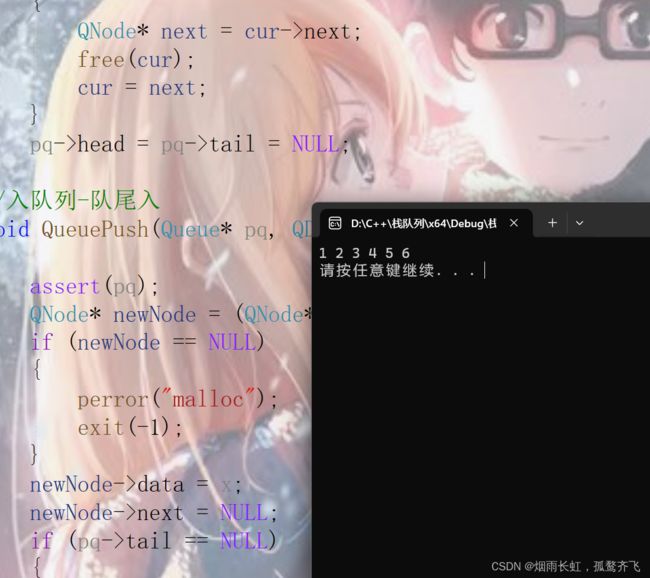
代码的测试
void TestQueue() { Queue q; QueueInit(&q); QueuePush(&q, 1); QueuePush(&q, 2); QueuePush(&q, 3); QueuePush(&q, 4); QueuePush(&q, 5); QueuePush(&q, 6); while (!QueueEmpty(&q)) { printf("%d ", QueueFornt(&q)); QueuePop(&q); } printf("\n"); QueueDestory(&q); } int main() { TestQueue(); system("pause"); return 0; }
代码的整体实现
#include#include #include #include typedef int QDataType; typedef struct QueueNode { struct QueueNode* next; QDataType data; }QNode; typedef struct Queue { QNode* head; QNode* tail; }Queue; void QueueInit(Queue* pq) { assert(pq); pq->head = pq->tail = NULL; } void QueueDestory(Queue* pq) { assert(pq); QNode* cur = pq->head; while (cur) { QNode* next = cur->next; free(cur); cur = next; } pq->head = pq->tail = NULL; } void QueuePush(Queue* pq, QDataType x) { assert(pq); QNode* newNode = (QNode*)malloc(sizeof(QNode)); if (newNode == NULL) { perror("malloc"); exit(-1); } newNode->data = x; newNode->next = NULL; if (pq->tail == NULL) { pq->head = pq->tail = newNode; } else { pq->tail->next = newNode; pq->tail = newNode; } } void QueuePop(Queue* pq) { assert(pq); assert(pq->head); if (pq->head->next == NULL) { free(pq->head); pq->head = pq->tail = NULL; } else { QNode* next = pq->head->next; free(pq->head); pq->head = next; } } QDataType QueueFornt(Queue* pq) { assert(pq); assert(pq->head); return pq->head->data; } QDataType QueueBack(Queue* pq) { assert(pq); assert(pq->head); return pq->tail->data; } int QueueaSize(Queue* pq) { assert(pq); int size = 0; QNode* cur = pq->head; while (cur) { ++size; cur = cur->next; } return size; } bool QueueEmpty(Queue* pq) { assert(pq); return pq->head == NULL; } void TestQueue() { Queue q; QueueInit(&q); QueuePush(&q, 1); QueuePush(&q, 2); QueuePush(&q, 3); QueuePush(&q, 4); QueuePush(&q, 5); QueuePush(&q, 6); while (!QueueEmpty(&q)) { printf("%d ", QueueFornt(&q)); QueuePop(&q); } printf("\n"); QueueDestory(&q); } int main() { TestQueue(); system("pause"); return 0; }
总结 :
<1>队列 是在队尾入队,队头出队,即两边都可操作
栈 的入栈和出栈都是在栈顶进行的,无法对栈底直接进行操作
<2>栈具有 后进先出 的性质,队列具有 先进先出 的性质
<3>栈就如一个杯子只能从栈顶开始遍历整个元素
队列就如一个空筒可从首尾两端遍历整个元素