leetcode - 296. Best Meeting Point

Description

Given an m x n binary grid grid where each 1 marks the home of one friend, return the minimal total travel distance.

The total travel distance is the sum of the distances between the houses of the friends and the meeting point.

The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.

Example 1:

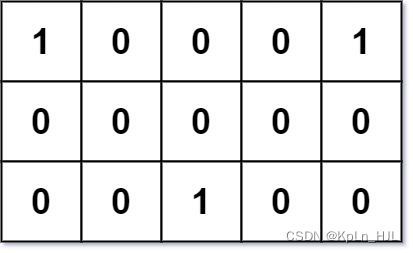
Input: grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]
Output: 6
Explanation: Given three friends living at (0,0), (0,4), and (2,2).
The point (0,2) is an ideal meeting point, as the total travel distance of 2 + 2 + 2 = 6 is minimal.
So return 6.

Example 2:

Input: grid = [[1,1]]
Output: 1

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 200
grid[i][j] is either 0 or 1.
There will be at least two friends in the grid.

Solution

The best meeting point would be, the median of all Xs and the median of all Ys.

Time complexity: $o(m\ast n)$
Space complexity: $o(m\ast n)$

Code

class Solution:
    def minTotalDistance(self, grid: List[List[int]]) -> int:
        def get_median(nums: list) -> float:
            # nums is sorted
            n = len(nums)
            if n % 2 == 0:
                return (nums[n // 2] + nums[n // 2 -1]) / 2
            else:
                return nums[n // 2]
        # get Xs in order
        m, n = len(grid), len(grid[0])
        xs = []
        for i in range(m):
            xs += [i] * sum(grid[i])
        # get Ys in order
        ys = []
        grid_transpose = list(zip(*grid))
        for j in range(n):
            ys += [j] * sum(grid_transpose[j])
        x_median, y_median = get_median(xs), get_median(ys)
        res = 0
        for xi in xs:
            res += abs(xi - x_median)
        for yi in ys:
            res += abs(yi - y_median)
        return int(res)