js递归回溯过程中究竟该传递n+1还是n+=1解析

今天是做回溯算法的第二天，碰到了两个题，第一个题一个小时解决，第二个题和第一个题非常类似，半个小时搞定，结果运行发现错误，又经过大半个小时才确定错误的原因——第一道题迭代时传递的参数中有一项是n+=1，于是第二道题也用了n+=1，结果就出现了错误，应该是n+1。于是就这个问题研究了半天，终于研究出了一丝规律。

首先先了解一下递归回溯的运行顺序规律：深度优先，由深到浅。什么意思呢，意思就是：在递归回溯中，优先补充组合内元素的数量(深度优先)，当数量达到终止条件之后经过判断，然后回溯删除掉最后一个元素，之后先考虑最后一个元素的其他可能，当没有其他可能之后再考虑倒数第二个元素的其他可能。(由深到浅)

以力扣216.组合总和III和17.电话号码的字母组合为例：

216代码及要点照片

let ans = []
        let arr = []
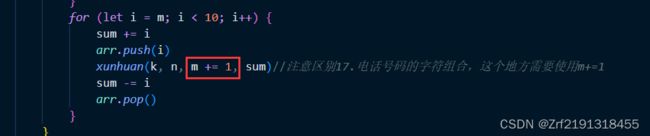
        let xunhuan = function (k, n, m, sum) {
            if (sum > n) {
                return
            }
            if (arr.length === k) {
                if (sum === n)
                    ans.push([...arr])
                return
            }
            for (let i = m; i < 10; i++) {
                sum += i
                arr.push(i)
                xunhuan(k, n, m += 1, sum)//注意区别17.电话号码的字符组合，这个地方需要使用m+=1
                sum -= i
                arr.pop()
            }
        }
        var combinationSum3 = function (k, n) {
            ans = []
            arr = []
            if (n > 45 || k > n) return ans
            xunhuan(k, n, 1, 0)
            return ans
        };
        combinationSum3(3, 7)

解析：了解了运行顺序规律之后，先看216这道题。将m+1作为参数传递时，递归函数中的m会加一，但是初始的m并没有改变。刚开始可能看不出差别，当最深层运行结束开始考虑倒数第二个元素的其他可能时，m就会起到作用——每进入一层递归，m的值就会加一，当开始考虑倒数第二个元素的其他可能时，m的值会减一，导致当考虑倒数第二个元素的其他可能时，进入递归添加最后一个数时会出现最后一个元素m+1还等于倒数第二个数，因为题目中要求的是不能重复，所以使用m+1会导致数据重复，而使用m+=1则可以保证即使开始考虑倒数第二个元素的其他可能，m也不会减一，进而保证数据不会重复。

17代码及要点照片

        var letterCombinations = function (digits) {
            let ans = [], path = ''
            let obj = {
                '2': ['a', 'b', 'c'],
                '3': ['d', 'e', 'f'],
                '4': ['g', 'h', 'i'],
                '5': ['j', 'k', 'l'],
                '6': ['m', 'n', 'o'],
                '7': ['p', 'q', 'r', 's'],
                '8': ['t', 'u', 'v'],
                '9': ['w', 'x', 'y', 'z'],
            }
            if (!digits.length) return ans
            xunhuan(digits, 0)
            return ans

            function xunhuan(n, a) {
                if (path.length === n.length) {
                    ans.push(path)
                    return
                }
                for (let b of obj[n[a]]) {
                    path += b
                    xunhuan(digits, a + 1)//该迭代要使用a+1，因为不仅在迭代中需要使用，在for循环中也需要使用，因此不能改变。
                    path = path.slice(0, -1)
                }
            }
        };

解析：看完216再来看这个题，运行过程就不分析了，是一模一样的，我们主要来看看这两个题的区别，216中m的使用是在递归过程中，不容易被观察到；但是在17题中，可以看到m出现在三个地方：形参、实参、被遍历的数据。注意这个被便利的数据，进程走到for循环中时，会有两条路，第一条就是进入递归，第二条就是递归返回后继续执行该循环。在递归过程中需要m的值加一是正常情况大家都了解的。但是在本题中，每个数字代表的字母不一样，因此被便利的数据就不能改变，因此只有a不变才可以保证被便利的数据不变。

结语：大家在做类似的递归回溯题时，一定要多debug几遍！多debug几遍！！多debug几遍！！！找找规律和错误的地方。