统计学|SPSS|主成分回归实例-发电站需求模型

前言：

由于spss并不能直接得到最终的主成分回归模型，以下以“发电站需求模型”一题为实例，进行利用spss进行的主成分回归

案例

题目

影响电的需求量的指标有：

(1)钢的产量x1; (2)生铁产量x2; (3)钢材产量x3; (4)有色金属产量x4;

(5)原煤产量x5; (6)水泥产量x6; (7)机械工业总产值x7; (8)化肥产量x8;

(9)硫酸产量x9; (10)烧碱产量x10; (11)棉纱产量x11

共11个指标。收集了23年的指标值，建立发电站需求模型。
数据如下：23年指标值，X1~X11为自变量，Y为电量需求

X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	X11	Y
47	56	48.3	7777	2028	32.2	7.31	0.3	1.21	1.43	26.2	10.7
62.6	110	59.6	13743	3500	33.2	9.61	1.8	2.28	1.93	28	17.7
68	125	60	12269	3800	55.6	12.85	3.3	5.39	1.9	27.6	26.8
35.3	57.6	25.6	4582	2600	24.4	6.76	10.6	5.36	1.54	11	24.2
31.3	20.6	23.5	3891	1296	17.9	5.08	13.7	5.61	1.33	10.2	20.1
35.2	18.2	26.5	5061	1052	24.8	5.54	16.9	7.51	1.47	14.2	19.3
45.3	23.7	38.5	7686	1001	37.8	7.14	34	8.64	1.57	20.4	22.9
49.5	28.2	50	9526	1134	78.8	11.2	60.8	13.87	1.92	26.6	28.9
59.7	30.5	69.2	10515	1545	101.6	15.89	103.9	20.05	2.86	33.2	39.1
47.8	19.6	52.7	7580	1287	74.9	10.86	88.1	15.75	2.41	23.9	39.1
17.7	8.1	17.2	2333	998	40.2	5.1	31.3	6.69	1.55	17.6	26.8
36	10.4	37.2	2099	1347	73.3	13.14	47.8	13.63	1.57	27.2	37.2
62	29.3	57.7	10589	1953	138.6	25.54	90.9	18.86	2.63	36.3	54.1
97	77.9	78.3	13004	2522	247	31.31	137.3	28.51	4	41.5	77.4
95.2	97.4	74.6	12593	2733	270	28.79	154	28.93	4.24	40.2	84
118.4	102.2	58.3	10936	2557	233.5	28.03	169.1	28.24	3.76	38.2	88.4
99.9	86.5	50	7810	2440	205	26.5	143.6	22.17	3.07	31.5	86.3
151	111	110.7	9400	3086	288	38.61	189	29.17	5.03	46.9	108
108	84.1	76.9	8476	2895	262.2	31.46	216.5	26.36	4.46	38.6	103
162.5	138.3	132	11632	3678	358.6	46.21	405.8	30.42	6.23	52.5	119
238.2	224	202	16163	3794	454.8	55.86	542.8	50	7.83	56	139
292.9	274.4	251.5	18796	3838	519.2	63.77	581.3	56.68	9.49	62.2	156
329	287.6	259.2	21300	3898	551.1	61.88	632.4	60.22	10.8	66.8	164

SPSS操作及分析

1. 相关性分析及主成分/公因子提取

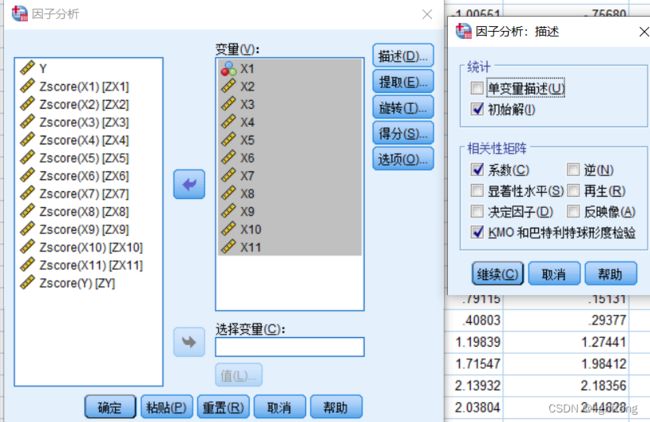
SPSS操作：分析-降维-因子

选取X1~X11为变量，描述选项勾选项如图所示

提取项选择如图：
由于进行主成分回归分析，为确保所有数据信息均被提取，在此不进行降维，因子数量与自变量数量一致，提取11个因子

旋转项：方法选择无，显示勾选荷载图

得分项：勾选显示因子得分系数矩阵

选项-勾选系数选择格式

结果

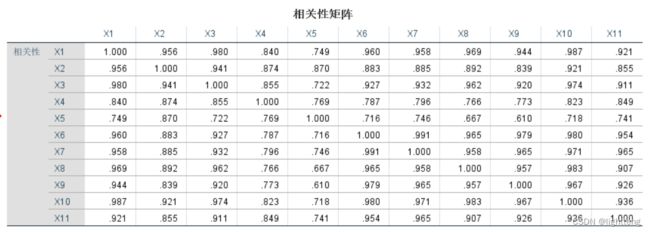
1. 相关性分析
因子分析需要变量间有相关性，所以首先要进行相关性检验，首先输出的是变量之间的相关系数矩阵。可以直观看到变量间是存在一定的相关性，如 X1 和 X3 相关性较大。

（1）相关性矩阵
（2）KMO和巴特利特检验

KMO统计量越接近1，变量间的相关性越强，偏相关性越弱，分析效果越好，一般KMO统计量小于0.3不适合做主成分分析，本次分析KMO=0.758，所以本例适合做主成分分析。
同时，巴特利特球形度检验统计量小于0.001，是显著的。
【备注】：
a. KMO统计量判断标准
b. 巴特利特球形度检验判断标准

2.提取主成分和公因子

在本例中，公因子方差数据，从表中最后一列可以看出所有原始变量均被提取信息。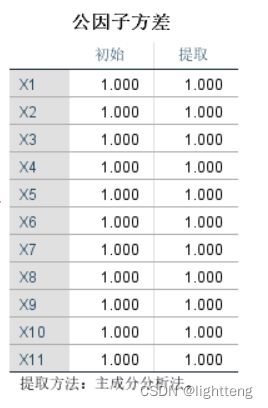

接下来输出主成分结果，表中第一列为11个成分，第二列总计项为对应的特征值，表示所解释的方差的大小，第三列为对应的成分所包含的方差占总方差的百分比，第四列为累计的百分比。

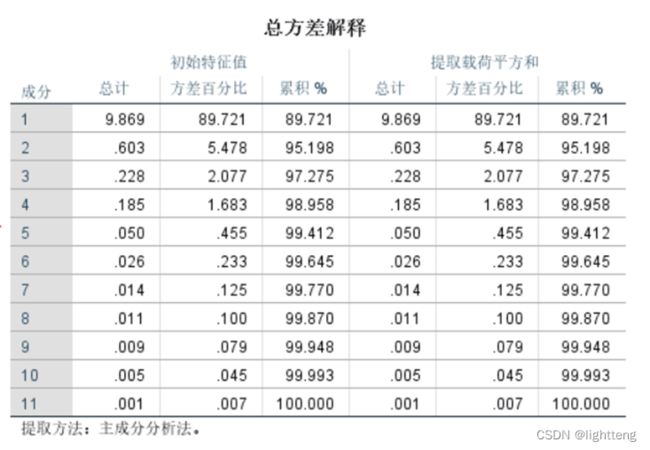
在本例中，成分1、成分2、成分3、成分4、成分5、成分6、成分7、成分8、成分9、成分10、成分11的特征值分别为9.869、0.603、0.228、0.185、0.050、0.260、0.014、0.011、0.009、0.005、0.001，合计能够解释100%的方差

接下来输出成分得分系数矩阵：

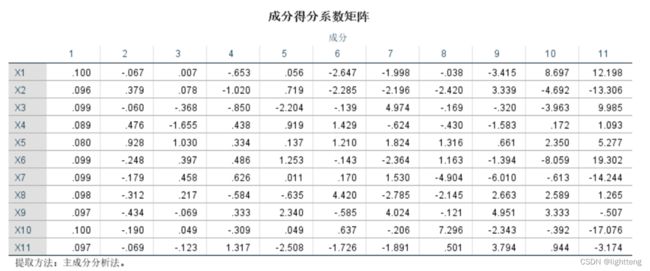
该因子载荷矩阵并不是主成分的特征向量，即不是主成分的系数。为了获取主成分系数，需要根据该矩阵除以特征根的平方根即可得到主成分表达式，

excel 操作

在excel中将spss中得到的成分得分系数矩阵分别除以对应特征根的平方根得到以下主成分得分系数矩阵：

变量	1	2	3	4	5	6	7	8	9	10	11
X1	0.31441	-0.05214	0.00318	-0.28104	0.01261	-0.42351	-0.23425	-0.00395	-0.31787	0.61026	0.33402
X2	0.30265	0.29449	0.03709	-0.43883	0.16076	-0.36564	-0.25747	-0.25323	0.31081	-0.32925	-0.36438
X3	0.31018	-0.04688	-0.17581	-0.36586	-0.49298	-0.02223	0.58310	-0.01771	-0.02978	-0.27810	0.27344
X4	0.27831	0.36951	-0.79106	0.18855	0.20570	0.22859	-0.07311	-0.04499	-0.14735	0.01204	0.02992
X5	0.25190	0.72029	0.49211	0.14353	0.03063	0.19356	0.21383	0.13775	0.06150	0.16491	0.14451
X6	0.31096	-0.19238	0.18984	0.20887	0.28023	-0.02281	-0.27705	0.12172	-0.12975	-0.56551	0.52856
X7	0.31153	-0.13880	0.21886	0.26924	0.00246	0.02725	0.17939	-0.51324	-0.55942	-0.04301	-0.39005
X8	0.30764	-0.24209	0.10351	-0.25121	-0.14215	0.70716	-0.32651	-0.22447	0.24790	0.18166	0.03465
X9	0.30340	-0.33688	-0.03307	0.14319	0.52358	-0.09358	0.47170	-0.01271	0.46088	0.23390	-0.01388
X10	0.31451	-0.14759	0.02362	-0.13297	0.01099	0.10184	-0.02412	0.76355	-0.21809	-0.02754	-0.46760
X11	0.30508	-0.05344	-0.05883	0.56659	-0.56101	-0.27617	-0.22168	0.05246	0.35321	0.06622	-0.08691

2. 主成分分析

SPSS操作

（1）数据描述：数据标准化
SPSS操作： 分析-描述统计-描述

选取X1~X11和Y，得到描述性统计结果，得到标准化数据，并另存为变量

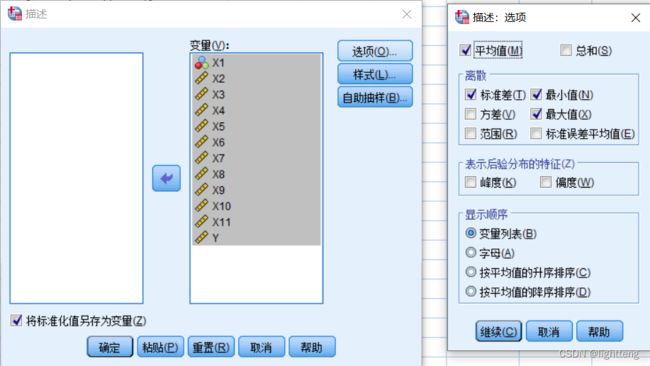
得到以下结果：得到这组数据的描述统计结果


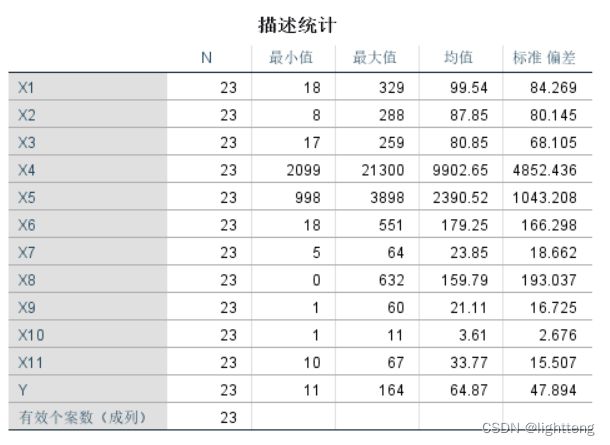
（2）计算主成分对应数据
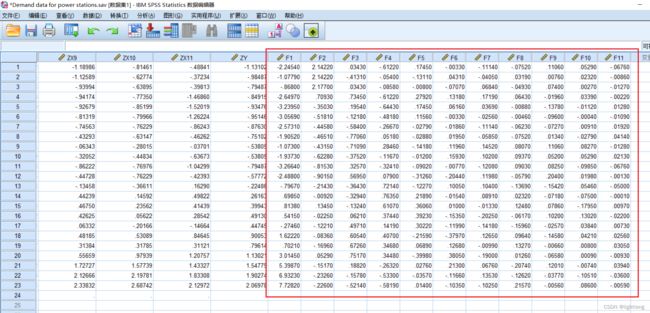
根据主成分得分矩阵，将标准化之后的数据代入，计算得出主成分对应数据（在excel中完成），并将F1~F11的数据黏贴到spss的数据集之中：

F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11
-2.2454	2.1422	0.0343	-0.6122	0.1745	-0.0033	-0.1114	-0.0752	0.1106	0.0529	-0.0676
-1.0779	2.1422	-0.4131	-0.0540	-0.1311	0.0431	-0.0405	0.0319	0.0076	0.0232	-0.0086
-0.8680	2.1770	0.0343	-0.0858	-0.0080	-0.0707	0.0684	-0.0493	0.0740	0.0027	-0.0127
-2.6497	0.7093	0.7345	-0.6122	0.2792	0.1318	0.1719	0.0643	-0.0196	0.0339	-0.0022
-3.2395	-0.3503	0.1954	-0.6443	0.1745	0.0616	0.0369	-0.0088	-0.1378	-0.0112	0.0128
-3.0569	-0.5181	-0.1218	-0.4818	0.1156	-0.0033	-0.0256	-0.0046	-0.0960	-0.0004	-0.0109
-2.5731	-0.4458	-0.5840	-0.2667	-0.0279	-0.0186	-0.1114	-0.0623	-0.0727	0.0091	0.0192
-1.9052	-0.4651	-0.7706	0.0518	-0.0288	0.0195	-0.0585	-0.0752	0.0134	-0.0279	0.0414
-1.0730	-0.4315	-0.7109	0.2846	-0.1418	0.1196	0.1452	0.0807	0.1106	0.0827	-0.0128
-1.9373	-0.6228	-0.3752	-0.1167	-0.0120	0.1593	0.1020	0.0937	0.0520	0.0529	0.0213
-3.2664	-0.8153	0.3257	-0.3241	-0.0902	-0.0077	-0.1208	0.0903	0.0825	-0.0985	-0.0676
-2.4880	-0.9015	0.5695	0.0790	-0.3126	-0.2044	0.1198	-0.0579	0.2040	0.0198	-0.0013
-0.7967	-0.2143	-0.3643	0.7214	-0.1227	0.1005	0.1040	-0.1369	-0.1542	0.0546	-0.0500
0.6985	-0.0092	-0.3294	0.7635	0.2189	-0.0154	0.0891	0.0232	-0.0718	-0.0750	-0.0001
0.8138	0.1345	-0.1324	0.6107	0.3606	0.0100	-0.0133	0.1248	0.0786	-0.1795	0.0097
0.5415	-0.0225	0.0621	0.3744	0.3923	-0.1535	-0.2025	-0.0617	0.1020	0.1302	-0.0220
-0.2746	-0.1221	0.4971	0.1419	0.3022	-0.1199	-0.1418	-0.1596	-0.0257	0.0384	0.0073
1.6222	-0.0836	0.6054	0.4070	-0.2159	-0.3797	0.1265	0.0964	-0.1458	0.0421	0.0256
0.7021	-0.1696	0.6726	0.3468	0.0689	0.1268	-0.0099	0.1327	-0.0066	0.0080	0.0305
3.0145	0.0529	0.7517	0.3448	-0.3998	0.3805	-0.1900	0.0126	-0.0658	0.0009	-0.0093
5.3987	-0.1517	0.1882	-0.2632	0.0276	0.2130	0.0676	-0.2074	0.1201	-0.0074	0.0394
6.9323	-0.2326	-0.1578	-0.5330	-0.0357	-0.1166	0.1353	-0.1262	-0.0377	-0.1051	-0.0360
7.7282	-0.2260	-0.5214	-0.5819	0.0140	-0.1035	-0.1025	0.2157	-0.0056	0.0860	-0.0059

（3）线性分析
1）用SPSS做出与1~11 的散点图
SPSS操作：图形-旧对话框-散点图/点图-矩阵散点图


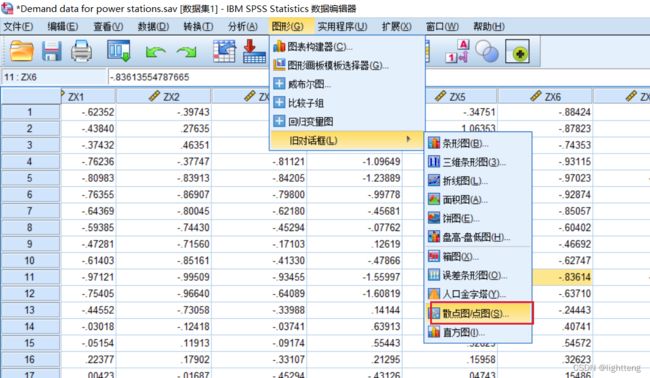
将F1~F11和ZY选为矩阵变量

输出：

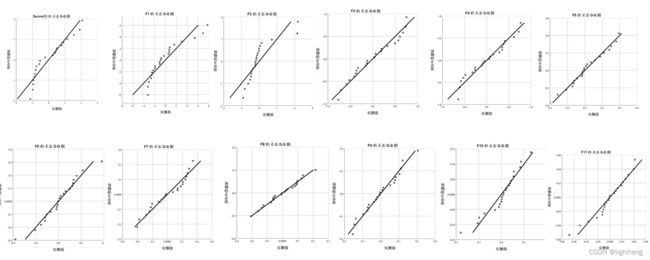
用SPSS做出ZY与1~11 的正态Q-Q图
SPSS操作：

输出：各正态Q-Q图，总共12个图，此处略，仅展示缩略图

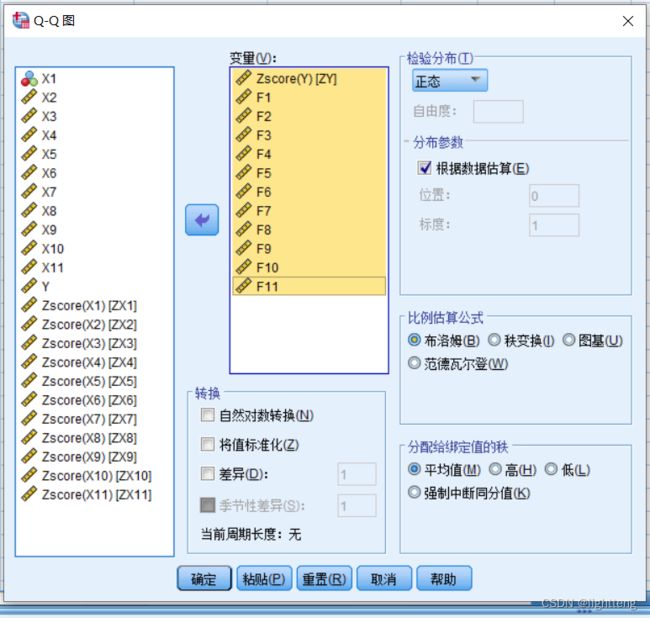
可以看出数据基本符合正态分布

2）线性回归
用SPSS中“分析-回归-线性”，设置ZY（Y标准化后）为因变量，F1~F11为自变量，选择步进，进行多元线性回归


输出



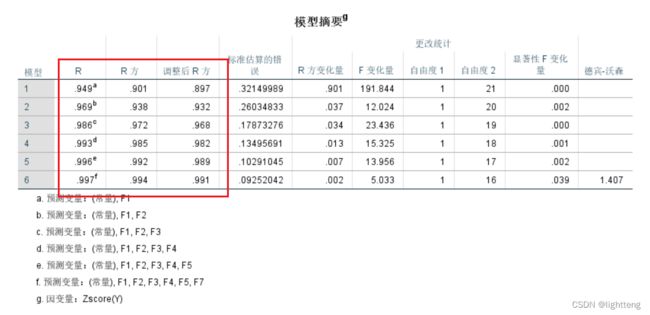
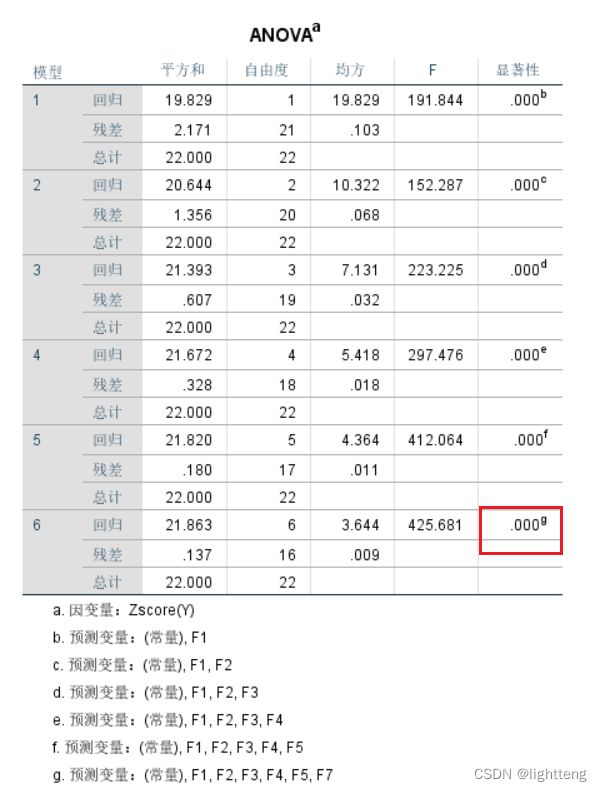
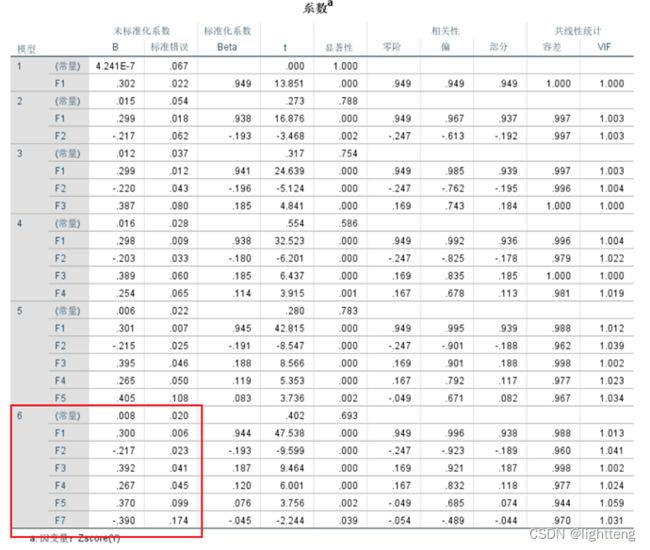
(a)
从系数表中，多元线性回归F6,F8,F9,F10和F11系数被剔除，F1,F2,F3,F4,F5,F7系数均显著。从共线性统计可以看出，没有共线现象。
根据系数表可写出估计的回归方程：
$$ZY=0.008+0.300\ast F_1-0.217F_2+0.392F_3+0.267F_4+0.370F_5-0.390F_7$$
即
$$Y=-10.594+0.073X_1+0.050X_2-0.333X_3-0.001X_4+0.004X_5+0.137X_6+0.545X_7+0.048X_8+0.570X_9+2.034X_{10}+0.340X_{11}$$

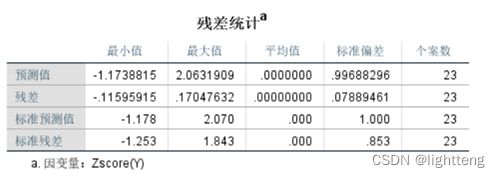
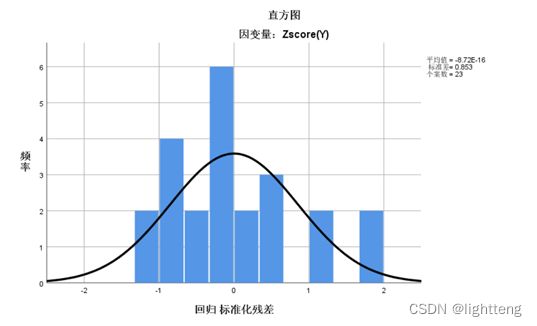
（b）模型检验-残差分析

写在最后

以上就是大致的过程，对数据的分析过程也许有所疏漏或者错误，望能指出，欢迎评论区交流~
后续也许能把计算的excel或者整理一份python代码，因为spss确实不算特别方便。