字符串匹配之BF算法、KMP算法
原始问题如下:
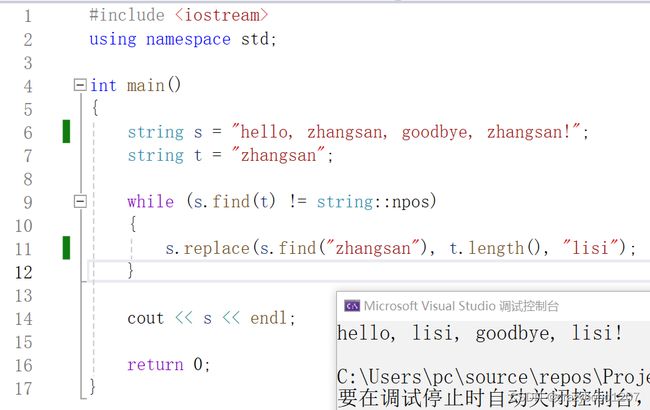
一个find就直接搞定了,数据结构书可以扔了,嘎嘎
咱不能做“调库侠”,还是看看具体怎么实现吧
先忽略字符串替换,暂时只解决字符串查找(匹配)问题
直接处理一个比较“大”的问题
主串:长度是1亿,所有字符都是a,有5个位置被修改为b
模式串:长度是10,aaaaaaaaab
查找结果:在主串的4个位置查找到了模式串(第一个b之前的字符a个数太少,无法匹配模式串)
方法1:直接调用c++ find方法
#include
using namespace std;
int main()
{
clock_t t1 = clock();
string t = "aaaaaaaaab";
string s(1e8, 'a');
s[5] = s[39] = s[9999] = s[1e6 + 4] = s[1e7 + 9] = 'b';
int start_pos = 0;
while (s.find(t, start_pos) != -1)
{
cout << "match_pos: " << s.find(t, start_pos) << endl;
start_pos = s.find(t, start_pos) + t.length(); //设置下一次查找的起始位置
}
clock_t t2 = clock();
double duration = double(double(t2) - double(t1)) / CLOCKS_PER_SEC;
cout << "用时: " << duration << "秒" << endl;
return 0;
} 方法2:稍微修改一下,速度快了一丢丢
#include
using namespace std;
int main()
{
clock_t t1 = clock();
string t = "aaaaaaaaab";
string s(1e8, 'a');
s[5] = s[39] = s[9999] = s[1e6 + 4] = s[1e7 + 9] = 'b';
int start_pos = 0;
int match_pos = s.find(t, start_pos);
while (match_pos != -1)
{
cout << "match_pos: " << match_pos << endl;
start_pos = match_pos + t.length(); //设置下一次查找的起始位置
match_pos = s.find(t, start_pos);
}
clock_t t2 = clock();
double duration = double(double(t2) - double(t1)) / CLOCKS_PER_SEC;
cout << "用时: " << duration << "秒" << endl;
return 0;
} 下面来自己实现find方法
方法3:BF算法,BF算法是暴力求解,速度比find方法慢。这个算法思想很简单:
(1)首先,为了访问主串和模式串,需要定义两个变量,即:下标i和j
(2)通过一个循环,依次比较主串字符和模式串字符,即:比较s[i]和t[j]
(3)如果s[i]和t[j]相等,那么,让i和j分别指向下一个字符,继续比较;如果s[i]和t[j]不相等,那么,重置i和j的值,然后重新尝试匹配
关键问题来了,i和j应该被重置为多少?很显然,模式串应该从它的第一个字符开始重新匹配,j应该重置为0。那么主串呢?
如果主串这次的匹配,是从主串的100位置开始比较的,那么当匹配失败时,下次匹配应该从101位置开始比较,所以i应该先退回到这次比较的开始位置100(主串应该从当前位置i往回退多少个字符呢?应该退回j个字符,因为这次匹配失败时,j的值等于已经匹配成功的字符个数,即i刚刚走过的字符个数),然后+1(即101)。
(4)如果循环结束后,j的值和t的长度相等,说明什么呢?刚才说过了,j的值等于已经匹配成功的字符个数,所以“j的值和t的长度相等”说明已经匹配成功的字符个数等于t的长度,即t已经匹配成功。
#include
#include
using namespace std;
int find_bf(const string& s, const string& t, int pos);
int times = 0;
int main()
{
clock_t t1 = clock();
string t = "aaaaaaaaab";
string s(1e8, 'a');
s[5] = s[39] = s[9999] = s[1e6 + 4] = s[1e7 + 9] = 'b';
int start_pos = 0;
int match_pos = find_bf(s, t, start_pos);
while (match_pos != -1)
{
cout << "match_pos: " << match_pos << endl;
start_pos = match_pos + t.length(); //设置下一次查找的起始位置
match_pos = find_bf(s, t, start_pos);
}
cout << "循环次数: " << times << endl;
clock_t t2 = clock();
double duration = double(double(t2) - double(t1)) / CLOCKS_PER_SEC;
cout << "用时: " << duration << "秒" << endl;
return 0;
}
int find_bf(const string& s, const string& t, int pos)
{
int i = pos, j = 0;
while (i < s.length() && j < t.length())
{
times++;
if (s[i] == t[j])
{
i++;
j++;
}
else
{
i = i - j + 1; //设置“下一轮比较,主串的起始位置”:j的值是已经匹配的字符个数,i-j表示主串先退回这次比较的起始位置,然后+1,即是下次比较的主串起始位置
j = 0; //设置“下一轮比较,模式串的起始位置”
}
}
if (j == t.length())
{
return i - j;
}
return -1;
} 方法4:KMP算法,经典的字符串匹配算法,和BF算法的区别主要在于,当匹配失败时,如何重置i和j的值,这个………要看动画演示,一看就懂。
为了比较KMP算法和BF算法的效率,增加了一个times变量,计算循环的次数,可以看到,KMP有效较少了循环的次数。一道数学题:手工计算这个循环次数?
#include
using namespace std;
void get_next(const string& t, int* next);
int find_kmp(const string& s, const string& t, int* next, int start_pos);
int times = 0;
int main()
{
clock_t t1 = clock();
string t = "aaaaaaaaab";
string s(1e8, 'a');
s[5] = s[39] = s[9999] = s[1e6 + 4] = s[1e7 + 9] = 'b';
int* next = new int[t.length()];
get_next(t, next);
int start_pos = 0;
int match_pos = find_kmp(s, t, next, start_pos);
while (match_pos != -1)
{
cout << "match_pos: " << match_pos << endl;
start_pos = match_pos + t.length(); //设置查找起始位置
match_pos = find_kmp(s, t, next, start_pos);
}
if (next != NULL)
{
delete[]next;
next = NULL;
}
cout << "循环次数: " << times << endl;
clock_t t2 = clock();
double duration = double(double(t2) - double(t1)) / CLOCKS_PER_SEC;
cout << "用时: " << duration << "秒" << endl;
return 0;
}
void get_next(const string& t, int* next)
{
next[0] = 0;
int i = 0;
int j = -1;
while (i < t.length() - 1)
{
if (j == -1 || t[i] == t[j])
{
i++;
j++;
next[i] = j;
}
else
{
j = next[j] - 1;
}
}
cout << "模式串" << t << "的next数组: ";
for (int i = 0; i < t.length(); i++)
{
cout << next[i] << " ";
}
cout << endl;
}
int find_kmp(const string& s, const string& t, int* next, int start_pos)
{
int i = start_pos;
int j = 0;
while (i < s.length() && j < t.length())
{
times++;
if (s[i] == t[j])
{
i++;
j++;
}
else
{
j = next[j];
if (j == 0)
{
i++;
j++;
}
}
}
if (j == t.length())
{
return i - j;
}
return -1;
} 按照1亿=10^8,循环2亿次,L1 cache访问时间0.8纳秒(4个时钟周期)来算,速度似乎到极限了。
方法5:KMP算法+多线程,因为主串的长度比较长,为了提高查找的速度,可以将主串分割成若干个子串,在每个子串中查找模式串。分割的时候要注意一个问题:模式串可能正好位于主串分割的边界处,因此分割的时候,要适当“放宽”子串的“右边界”,防止“漏网之鱼”。
另外,为了追求运行速度,不再使用c++的string类型,改用c语言的char类型。线程数取决于自己的cpu核心数,如果是8核心16线程的cpu,线程数可以设置为16,如果是16核心32线程的cpu,线程数可以设置为32,更多的线程数基本不会提高程序运行速度。
主串有6个位置设置为字符b,最后在主串的5个位置查找到了模式串(除了第一个字符b,它前面的字符a个数太少)
#include
#include
using namespace std;
void get_next(const char* t, int* next);
int find_kmp(const char* s, const char* t, const int* next, int start_pos, int end_pos);
void find_kmp_thread(const char* s, const int* pos, const char* t, const int* next, int tid);
const int THREADNUM = 32;
int main()
{
clock_t t1 = clock();
const char* t = "aaaaaaaaab"; //模式串,长度是10
const int string_length = 1e8; //主串,长度是1亿,所有字符几乎都是a
char* s = new char[string_length];
memset(s, 'a', string_length);
s[5] = s[39] = s[9999] = s[1000004] = s[10000009] = s[string_length - 1] = 'b'; //主串中6个位置的b被修改为a
int* next = new int[strlen(t)];
get_next(t, next);
int blockSize = int(string_length / THREADNUM); //分割主串,然后多线程调用kmp算法
int pos[THREADNUM + 1] = { 0 };
pos[THREADNUM] = string_length;
if (THREADNUM > 1)
{
for (int i = 1; i < THREADNUM; i++)
{
pos[i] = blockSize * i;
}
}
thread td[THREADNUM];
for (int i = 0; i < THREADNUM; i++)
{
td[i] = thread(&find_kmp_thread, s, pos, t, next, i);
}
for (int i = 0; i < THREADNUM; i++)
{
td[i].join();
}
if (next != NULL)
{
delete[]next;
next = NULL;
}
clock_t t2 = clock();
double duration = double(double(t2) - double(t1)) / CLOCKS_PER_SEC;
cout << "用时: " << duration << "秒" << endl;
return 0;
}
void find_kmp_thread(const char* s, const int* pos, const char* t, const int* next, int tid)
{
int start_pos = pos[tid];
int end_pos;
if (tid == THREADNUM - 1)
{
end_pos = pos[tid + 1];
}
else
{
end_pos = pos[tid + 1] + strlen(t) - 1; //防止模式串正好位于(两个线程处理的字符串的)边界位置
}
int match_pos = find_kmp(s, t, next, start_pos, end_pos);
while (match_pos != -1)
{
cout << "match_pos: " << match_pos << endl;
start_pos = match_pos + strlen(t); //设置查找起始位置
match_pos = find_kmp(s, t, next, start_pos, end_pos);
}
}
void get_next(const char* t, int* next)
{
next[0] = 0;
int i = 0;
int j = -1;
while (i < strlen(t) - 1)
{
if (j == -1 || t[i] == t[j])
{
i++;
j++;
next[i] = j;
}
else
{
j = next[j] - 1;
}
}
cout << "模式串" << t << "的next数组: ";
for (int i = 0; i < strlen(t); i++)
{
cout << next[i] << " ";
}
cout << endl;
}
int find_kmp(const char* s, const char* t, const int* next, int start_pos, int end_pos)
{
int i = start_pos;
int j = 0;
while (i < end_pos && j < strlen(t))
{
if (s[i] == t[j])
{
i++;
j++;
}
else
{
j = next[j];
if (j == 0)
{
i++;
j++;
}
}
}
if (j == strlen(t))
{
return i - j;
}
return -1;
} 最后,在一亿个字符的主串中查找长度为10的模式串,用时0.058秒。多线程加速效果只有3倍,数据量大的话,加速效果应该会更明显。
还有别的字符串匹配算法,时间复杂度略有区别。