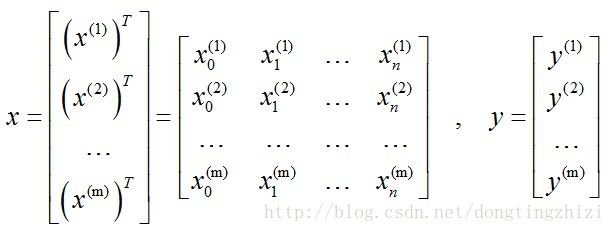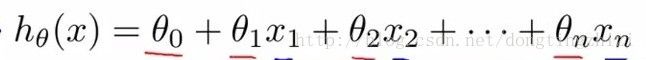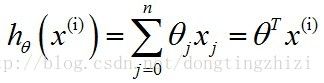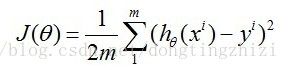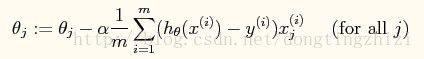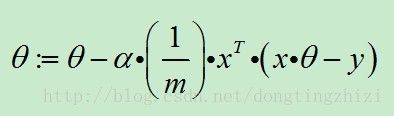回归问题总结(梯度下降、线性回归、逻辑回归、源码、正则化)
原文地址:http://blog.csdn.net/gumpeng/article/details/51191376
最近,应妹子要求,对回归问题进行了总结。
网上相关资料很多,主要是针对Andrew Ng的在线课程写的笔记, 但大部分都讲得不清晰。这篇博客不能算是原创,主要是将我认为比较好的博客做了汇总,按照我觉得比较容易看懂的方式进行排版。希望能对大家有帮助。
有兴趣的同学也可以根据文章最后的参考文献,去看看原来博主的文章。
1、线性回归
1.1 基本原理
在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。
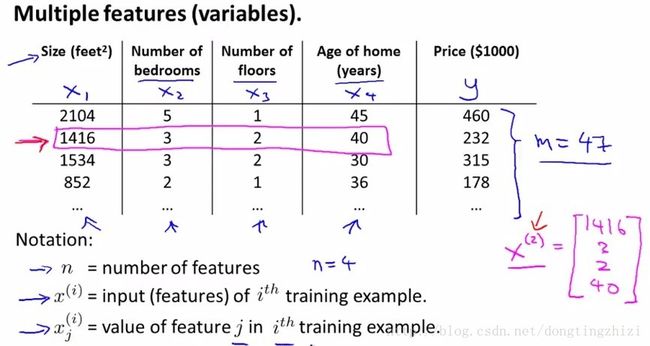
例如Andrew Ng老师的课程中给的房价预测的例子,影响房价的因素有n个,如下图:
每个因素即为一个特征,每个训练样本有n个特征。
一般表示格式按如下约定,第i条样本的输入x(i):
所有训练样本的输入表示为x,输出表示为y,共有m个输入:
θ就是我们要求的回归参数,因为是线性回归,所以为没个特征x(i)添加一个参数θ(i),所以h函数的形式如下:
为了公式表示方便,将x0设定为1,同时将所有θ表示成向量:
则有:
linear regression中一般将J函数(打分函数据)取成如下形式:
至于为什么取成该式,这里不进行深入的分析和推导,网上有一篇文章《Standford机器学习+线性回归CostFunction和Normal+equation的推导》进行了推导,可供参考。
用梯度下降法求J(θ)的最小值,梯度下降法就是如下的过程(α表示学习率):
a、对于多个特征:
对于上面给出的J(θ),有:
所以θ的迭代公式为:
b、对于单个特征
当单个特征值时,上式中j表示系数(权重)的编号,右边的值赋值给左边θj从而完成一次迭代。
上式就是批梯度下降算法(batch gradient descent),当上式收敛时则退出迭代,何为收敛,即前后两次迭代的值不再发生变化了。一般情况下,会设置一个具体的参数,当前后两次迭代差值小于该参数时候结束迭代。注意以下几点:
# coding=utf-8
#!/usr/bin/python
#Training data set
#each element in x represents (x0,x1,x2)
x = [(1,0.,3) , (1,1.,3) ,(1,2.,3), (1,3.,2) , (1,4.,4)]
#y[i] is the output of y = theta0 * x[0] + theta1 * x[1] +theta2 * x[2]
y = [95.364,97.217205,75.195834,60.105519,49.342380]
epsilon = 0.000001
#learning rate
alpha = 0.001
diff = [0,0]
error1 = 0
error0 =0
m = len(x)
#init the parameters to zero
theta0 = 0
theta1 = 0
theta2 = 0
sum0 = 0
sum1 = 0
sum2 = 0
while True:
#calculate the parameters
for i in range(m):
#begin batch gradient descent
diff[0] = y[i]-( theta0 + theta1 * x[i][1] + theta2 * x[i][2] )
sum0 = sum0 + alpha * diff[0]* x[i][0]
sum1 = sum1 + alpha * diff[0]* x[i][1]
sum2 = sum2 + alpha * diff[0]* x[i][2]
#end batch gradient descent
theta0 = sum0;
theta1 = sum1;
theta2 = sum2;
#calculate the cost function
error1 = 0
for lp in range(len(x)):
error1 += ( y[i]-( theta0 + theta1 * x[i][1] + theta2 * x[i][2] ) )**2/2
if abs(error1-error0) < epsilon:
break
else:
error0 = error1
print ' theta0 : %f, theta1 : %f, theta2 : %f, error1 : %f'%(theta0,theta1,theta2,error1)
print 'Done: theta0 : %f, theta1 : %f, theta2 : %f'%(theta0,theta1,theta2)1.2 随机梯度下降
因为每次计算梯度都需要遍历所有的样本点。这是因为梯度是J(θ)的导数,而J(θ)是需要考虑所有样本的误差和 ,这个方法问题就是,扩展性问题,当样本点很大的时候,基本就没法算了。所以接下来又提出了随机梯度下降算法(stochastic gradient descent )。随机梯度下降算法,每次迭代只是考虑让该样本点的J(θ)趋向最小,而不管其他的样本点,这样算法会很快,但是收敛的过程会比较曲折,整体效果上,大多数时候它只能接近局部最优解,而无法真正达到局部最优解。所以适合用于较大训练集的case。
随机梯度下降的代码如下:
# coding=utf-8
#!/usr/bin/python
#Training data set
#each element in x represents (x0,x1,x2)
x = [(1,0.,3) , (1,1.,3) ,(1,2.,3), (1,3.,2) , (1,4.,4)]
#y[i] is the output of y = theta0 * x[0] + theta1 * x[1] +theta2 * x[2]
y = [95.364,97.217205,75.195834,60.105519,49.342380]
epsilon = 0.0001
#learning rate
alpha = 0.01
diff = [0,0]
error1 = 0
error0 =0
m = len(x)
#init the parameters to zero
theta0 = 0
theta1 = 0
theta2 = 0
while True:
#calculate the parameters
for i in range(m):
diff[0] = y[i]-( theta0 + theta1 * x[i][1] + theta2 * x[i][2] )
theta0 = theta0 + alpha * diff[0]* x[i][0]
theta1 = theta1 + alpha * diff[0]* x[i][1]
theta2 = theta2 + alpha * diff[0]* x[i][2]
#calculate the cost function
error1 = 0
for lp in range(len(x)):
error1 += ( y[i]-( theta0 + theta1 * x[i][1] + theta2 * x[i][2] ) )**2/2
if abs(error1-error0) < epsilon:
break
else:
error0 = error1
print ' theta0 : %f, theta1 : %f, theta2 : %f, error1 : %f'%(theta0,theta1,theta2,error1)
print 'Done: theta0 : %f, theta1 : %f, theta2 : %f'%(theta0,theta1,theta2)
1.3 Feature scaling
Feature scaling可以通俗的解释为:将不同特征的取值转换到差不多的范围内。因为不同特征的取值有可能有很大的差别(几个数量级),例如下图中的x1和x2差别就非常大。这样会带来什么后果呢?从左图中可以看出,θ1-θ2的图形会是非常狭长的椭圆形,这样非常不利于梯度下降(θ1方向会非常“敏感”,或者说来回“震荡”)。进行scaling处理后,不同特征的规模相似,因此右图中的θ1-θ2图形会近似为圆形,这样更加适合梯度下降算法。

使用(3)中标准差的方法对前面的训练样本x矩阵进行归一化的代码如下:
1.4 vectorization