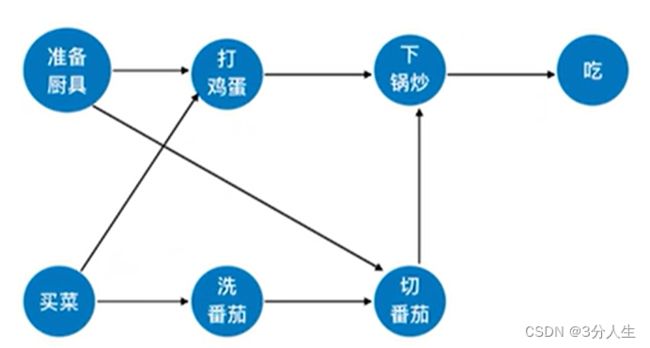
拓扑排序算法

操作对象：AOV网的点和边

有向无环图：有向图且不会形成回路

AOV网：在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，称为AOV网

拓扑排序：在图论中由一个有向无环图的顶点组成的序列中，当且仅当满足以下条件时，称为该图的一个拓扑排序：

1.每个顶点出现且只出现一次

2.若顶点A在序列中排在顶点B的前面，则在图中不存在顶点B到顶点A的路径

拓扑排序的实现

1.从AOV网中选择一个没有前驱的顶点并输出。

2.从网中删除该顶点和所有以它为起点的有向边

3.重复1和2直到当前的AOV网中不存在无前前驱的顶点为止

拓扑排序的实现一般用邻接表来储存图，实现的时间复杂度为O(n+e)，一般还需要用一个栈来储存入度为0的点。

个人从题目中发现拓扑排序有点递推的意思。

洛谷 P4017 最大食物链计数

题目背景

你知道食物链吗？Delia 生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。

题目描述

给你一个食物网，你要求出这个食物网中最大食物链的数量。

（这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者。）

Delia 非常急，所以你只有 1 秒的时间。

由于这个结果可能过大，你只需要输出总数模上80112002 的结果。

输入格式

第一行，两个正整数 n、m，表示生物种类 n 和吃与被吃的关系数 m。

接下来 m 行，每行两个正整数，表示被吃的生物A和吃A的生物B。

输出格式

一行一个整数，为最大食物链数量模上 8011200280112002 的结果。

输入输出样例

输入 #1

5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4

输出 #1

5

说明/提示

各测试点满足以下约定：

【补充说明】

数据中不会出现环，满足生物学的要求。（感谢 @AKEE ）

解题思路

由题目条件知道本题的图是一个有向无环图，1.满足使用拓扑排序的要求，2求路径数，出度为零的点的路径总和就是答案，生产者就是入度为零的点，从删除生产者这个点，生产者这个点会给吃他的那个点提供一条路径，而吃生产者的那个点又会给吃吃生产者的这个点提供一条路径，是不是有点递推的意思了，而拓扑排序在删除入度为零的点就执行这个操作，直到将所有点删除，然后出度为0的点的路径和就是答案

本题我用的是邻接矩阵储存图，当然也可以用邻接表储存

#include
//book标记出度不为0的点，du数组记录每个点的入度，dp数组记录到每个点i的路径数（生物链数）
int du[5001] = { 0 },  dp[5001], book[5001];
int a[5001][5001];//存储图
int top = 1, queck[50001];//栈存储入度为0的点
int main()
{
	int i, n, m, x, y;
	scanf("%d %d", &n, &m);
	for (i = 1; i <= m; i++)
	{
		scanf("%d %d", &x, &y);
		a[x][y] = 1;//x到y这个点有路径
		du[y]++;//y这个点入度+1
		book[x] = 1;//标记出度不为0的点
	}
	for (i = 1; i <= n; i++)//找到入度为0的点
	{
		if (du[i] == 0)
		{
			queck[++top] = i;
			dp[i] = 1;//入度为0的点起始算有一条食物链
		}
	}
	while (top > 0)//栈不为空
	{
		int k = queck[top];
		top--;//栈顶出队
		for (i = 1; i <= n; i++)//遍历k能到的点，
		{
			if (a[k][i] == 1)//如果k到i这个点有路径，i吃k
			{
				dp[i] = (dp[i] + dp[k]) % 80112002;
				du[i]--;//删除k这个点使得i这个点的入度减少1
				if (du[i] == 0)//如果这个点入度为0，入栈
					queck[++top] = i;
				a[k][i] = 0;//销毁路径
			}
		}
	}
	int sum = 0;
	for (i = 1; i <= n; i++)//统计路径总数
		if (book[i] == 0)
			sum = (sum + dp[i]) % 80112002;
	printf("%d", sum);
	return 0;
}

用邻接矩阵储存图时，n个点入栈出栈，每一个点遍历n，可知时间复杂度为O(n^2)

洛谷 P1807 最长路

题目描述

设 G 为有 n 个顶点的带权有向无环图，G 中各顶点的编号为 1 到 n，请设计算法，计算图 G 中 1,n 间的最长路径。

输入格式

输入的第一行有两个整数，分别代表图的点数 n 和边数 m。

第 2 到第 (m+1) 行，每行 3 个整数 u,v,w（u

输出格式

输出一行一个整数，代表 1 到 n 的最长路。

若 1 无法到达 n，请输出 −1。

输入输出样例

输入 #1

2 1
1 2 1

输出 #1

1

说明/提示

【数据规模与约定】

• 对于 20%的数据，n≤100，m≤10^3。
• 对于 40% 的数据，n≤10^3，m≤10^4。
• 对于 100% 的数据，1≤n≤1500，0≤m≤5×10^4，1≤u,v≤n，-10^5≤w≤10^5。

 这题两个坑：

1.边权值可能为负数，不适用迪杰斯特拉算法，

2.如果用拓扑排序算法的话需要将不为点不为1且入度为零的点删除而且不是只去除外围一层，而是多层的，原因就是如果你不废除那些除了一之外的入读为零的节点，你如果从一号点开始搜的话，如果那个点有初度，你的一号点所达到的那个点可能就永远都有入度，就永远不可能收入栈

#include
int u[50001], v[50001], w[50001];//u为起始点，v为终点，w为u->v的权值
int first[1501], next[50001];//first存储每个点的第一条边的位置
int book[1501];
int n, m, sum = 0, flag = 0, max = -1e9;
void dfs(int x)
{
	book[x] = 1;
	int k = first[x];
	while (k != 0)
	{
		if (book[v[k]] == 0)//值为0代表没有边
			dfs(v[k]);
		k = next[k];
	}
}
int maxs(int x, int y)//max函数返回较大值
{
	if (x > y)return x;
	else 
		return y;
}
int qu[1501], top = 0, du[1501], dp[1501];
int main()
{
	int i;
	scanf("%d %d", &n, &m);
	for (i = 1; i <= m; i++)
	{
		scanf("%d %d %d", &u[i], &v[i], &w[i]);
		du[v[i]]++;//入度加一
		//模拟邻接表
		next[i] = first[u[i]];
		first[u[i]] = i;
	}
	book[1] = 1;//标记1点
	dfs(1);//dfs搜索
	if (book[n] == 0)//如果不能到达n
	{
		printf("-1");//输出-1
		return 0;
	}
	//清除不为1且入度为0的点
	for (i = 2; i <= n; i++)
	{
		if (du[i] == 0)
			qu[++top] = i;
		//初始除去1点外的距离为无穷小，因为存在负权边
		//在取得某点的最长路长度时很有可能是一个负数，如果用0来赋初值的话，
		// 0会盖过原来正确的长度使得所求值偏大
		dp[i] = -1e9;
	}
	while (top > 0)
	{
		int k = first[qu[top]];
		top--;
		while (k != 0)
		{
			du[v[k]]--;
			if (du[v[k]] == 0)
				qu[++top] = v[k];
			k = next[k];
		}
	}

	top = 1; qu[1] = 1;//1这个点入栈
	while (top > 0)
	{
		int k = first[qu[top]];
		top--;
		while (k != 0)
		{
			du[v[k]]--;
			dp[v[k]] = maxs(w[k] + dp[u[k]], dp[v[k]]);//求最长路，递推取较大值，
			if (du[v[k]] == 0)//如果入度减少为零入栈
				qu[++top] = v[k];
			k = next[k];
		}
	}
	printf("%d", dp[n]);//输出最长路
	return 0;
}

本题我用的是模拟邻接表（链式向前星）储存图，拓扑排序算法时间复杂度为O(n+e)

判断1能否到达n采用一次dfs搜索能否将book[n]标记，若能代表能够到达，递推每次取能到达这个点的最大值