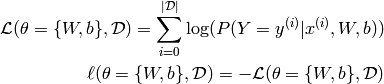Logistic Regression 之手写数字识别

 

0. 前言

  本文是应用 logsitic regression 模型对手写数字识别的实现，整个程序是基于 MNIST 手写数字数据库进行 train， cross validate 和 test 的，如需下载 python 实现的源代码，请点击这里，你还可以在这里下载数据集。 MNIST 数据库由NYU 的 Yann LeCun 等人维护， Yann LeCun 自 1998 年以来就一直从事这方面的研究，实现的方法包括 linear classifier， K-NN， SVM， CNN 等，他提出的卷积神经网络是第一个真正多层结构学习算法，利用空间相对关系减少参数数目以提高训练性能，咱手写数字识别的第三种方法就是基于这个算法滴，Yan LeCun 同志曾经在深度机器学习大神 Geoffrey E. Hinton 底下做过博士后，现在也是 deep learning 的一个领军人物了。

  言归正转，要用 python 实现这个项目还得用到 python 里面一个比较特殊的 deep learning 的库—— Theano, 初次接触这个库，理解起来还需要一点时间，比如说 GPU 加速处理时，你需要将向量块结构的变量转换为 shared variables, 比如说类似于函数作用的 Graph structure, 学习曲线稍显陡峭，如果你现在编程暂时用不到这些，直接跳过也行。

1. MNIST 相关

  动手之前，我们要先了解一下 MNIST 的相关情况。MNIST 包含了 7w 张 28×28 pixels 大小、数字 size 已经归一化 (标准是什么？是每类数字外面轮廓框框的大小吗？)、中心化( maybe 框框的中心)的图片。 deep learning tutorial 已经把它分为 train set, validation set and test set 3 个部分，分别包含了 5w、 1w 和 1w 张图片。你如果一定要自己亲眼瞅一瞅，跑一跑下面的代码，看一看 train set 上第 0 张图片长啥样：

 1 import cPickle

 2 import gzip

 3 

 4 import numpy

 5 import Image

 6 

 7 f = gzip.open('../data/mnist.pkl.gz', 'rb')

 8 train_set, valid_set, test_set = cPickle.load(f)

 9 f.close()

10 

11 print "The 0'th label:", train_set[1][0]

12 lst = numpy.asarray(train_set[0][0], dtype=numpy.float32)

13 img = Image.fromstring(mode='F', size=(28, 28), data=lst*255)

14 img.show()

  不出意外的话，第 0 张训练图片应该是 5, label 也是 5:

The 0'th label: 5

2. 梯度下降

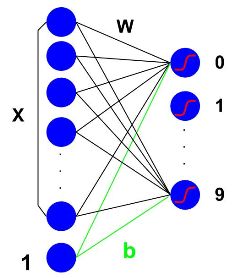
  首先，本次实验的 logistic regression 框架可以用下面这张图来表示（ logistic regression 基础知识请参考上篇文章）：

x: 28*28 个 pixels作为 784 个输入节点

w: 输入节点的权重

b: bias 项的权重

0~9: 输出节点

      此次实验的优化方法采用的是梯度下降法。梯度下降法中我们熟知的是标准的梯度下降算法 (ordinary gradient descent)， 即每次迭代需要计算基于所有 datapoint 的 loss function 的 gradient， 计算量很大，速度较慢，而且因为标准误差曲面只有一个，如果存在多个极小值点，此算法容易陷于局部极小值。同时还有另外一种比较高效的方法是 SGD (stochastic gradient descent)， 这种方法 estimating the gradient from just a few examples at a time instead of the entire training set. 由于每次计算 gradient 的时候每个误差曲面是不同的，它们不一定具有相同的极小值，所以有时可以避免局部极小值 （这是我的直观理解）。A stationary point with respect to the error funciton for the whole data set will generally not be a stationary point for each data point individually (Bishop PRML). 在这个程序中，考虑到 shared variable 的特点，我们采用的是类似 SGD 的 Minibatch SGD ，每次迭代是基于好几百个 examples 的梯度计算。

  同时，由于我们采用的是梯度下降策略，并不要求 Hessian 矩阵是可逆的，所以损失函数无需 weight decay 项，直接最小化最大似然函数的负对数即可，当然，这种方法可能导致的后果是最优解不是唯一的，并且容易产生 overfitting （这里采用了 early-stopping 方法解决这个问题）。对于某一次 batch of train set 来说， Loss Function 可以写成：

  Logistic Regression 模型建立的代码如下：

 1 ####################

 2 #Build Actual Model#

 3 ####################

 4 

 5 # allocate symbolic variables for the data

 6 index = T.lscalar()  # index to a [mini]batch

 7 x = T.matrix('x')  # the data is presented as rasterized images

 8 y = T.ivector('y')  # the labels are presented as 1D vector of [int] labels

 9 

10 # 创建之前定义的 LR 类，这里没有写出来。

11 # 类里面初始化了 w， b 为全零向量

12 # 按照 LR 的结构建立了从 inputs 到 outputs 的 graph structure。

13 classifier = LogisticRegression(input=x, n_in=28 * 28, n_out=10)

14 

15 # 输入 batch 的 index， 函数按照 index 将数据块传递给 x， 

16 # x 作为 classfier 的默认参数进入 LogisticRegression 类处理流程

17 # 最后输出错误分类的点的数目

18 # 整个过程就像 pipes

19 test_model = theano.function(inputs=[index],

20         outputs=classifier.errors(y),

21         givens={

22             x: test_set_x[index * batch_size: (index + 1) * batch_size],

23             y: test_set_y[index * batch_size: (index + 1) * batch_size]})

24 

25 validate_model = theano.function(inputs=[index],

26         outputs=classifier.errors(y),

27         givens={

28             x: valid_set_x[index * batch_size:(index + 1) * batch_size],

29             y: valid_set_y[index * batch_size:(index + 1) * batch_size]})

30 

31 # 求梯度，直接调用函数

32 g_W = T.grad(cost=cost, wrt=classifier.W)

33 g_b = T.grad(cost=cost, wrt=classifier.b)

34 

35 updates = [(classifier.W, classifier.W - learning_rate * g_W),

36            (classifier.b, classifier.b - learning_rate * g_b)]

37 

38 cost = classifier.negative_log_likelihood(y)

39 

40 # 数据先利用 givens 得到数据块

41 # 然后进入类求得 cost 函数

42 # 最后利用 update 将权重更新

43 train_model = theano.function(inputs=[index],

44         outputs=cost,

45         updates=updates,

46         givens={

47             x: train_set_x[index * batch_size:(index + 1) * batch_size],

48             y: train_set_y[index * batch_size:(index + 1) * batch_size]})

3. Early Stopping

  Early stopping是应对 overfitting 的方法之一。主要思路如下：先用 train set 将 model 进行训练，然后用得到的 model 来预测 validation set， 预测效果可以用 error 来表示。如果 error 在减小，说明我们的模型还可以继续训练，当 error 增大的时候，很有可能我们的 model 就 overfitting 了，这时候优化算法就应该 halts 了。但是有一个问题是 “increasing validation error” is ambiguous， 很有可能是整体先下降再上升，但是在局部上表现为 up and down， 就像股票走势一样。要解决这个问题，可以一开始我们就把 model 训练到全局极小值，然后对这个过程中的每一次迭代进行 validation error 的计算，这样做虽然很安全，但是损失了 early stopping 快速的优点。这里，我们采用的方法是：计算每一次迭代中 validation error， 如果比上次至少降低了 0.05%， 说明效果可以，就可以将迭代的限制次数增加到本次迭代次数的两倍。显然，这是一个基于经验的办法。

  训练模型的重要参数：

1. epoch: 默认在整个 train set 层次上训练轮数低于 1000
2. practice: 默认在 batch 层次上最少的迭代次数是 5000, 如果 model 在 validation set 上表现效果好，可以增加到目前迭代次数的 2 倍
3. validation_frequency: 每隔多少个 batch 评价一下 model， model 效果提升了，就可以增加 batch 的迭代限制次数。

  最后，由于 model 是 基于 validation set 上的最小错误率选出来的，因此，validation set 对于这个 model 来说是有偏的。换句话说， 选出来的模型会比较契合你现在的 validation set，所以不能用它来表示你模型的准确度，于是乎，我们又划分出一个 model 从来没有见过的 test set，用它的 error 来表示最终的预测能力。根据 Andrew Ng 的课程， train set : validation set : test set = 6 : 2 : 2, 这里，我们用的是 5 : 1 : 1.

  模型训练的代码如下:

1 #############

2 #Train Model#

3 #############

4 epoch = 0

5 while (epoch < n_epochs) and (not done_looping):

6         epoch = epoch + 1

7         for minibatch_index in xrange(n_train_batches):

8                 minibatch_avg_cost = train_model(minibatch_index)

9 ....

 

 由于代码比较简单，这里不做详细解析了，详细步骤请参考这里的最后。

  用 logistic regression 的方法，可以将 test set 上的错误率降低到 7.489583 %。

4. Load and Save Models

  辛辛苦苦把 model 训练好了，千万不能忘记保存啊，这样，下次一个新数据过来的时候，我们就可以直接进行判断啦。

 

 

---

参考资料：

[1]: http://deeplearning.net/tutorial/logreg.html

[2]: Early-stopping