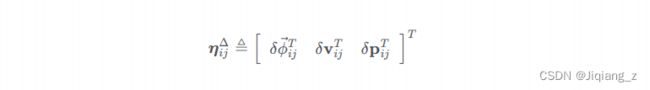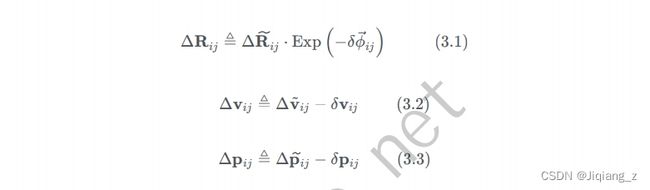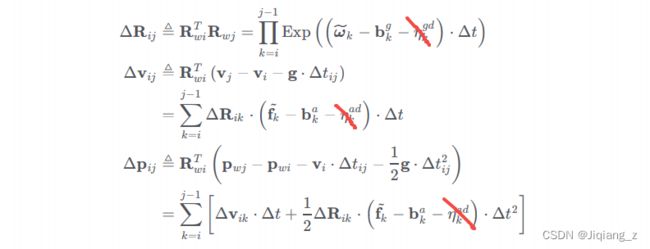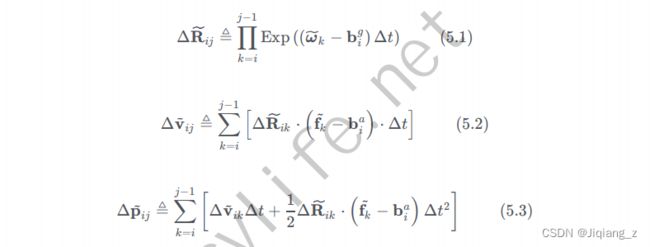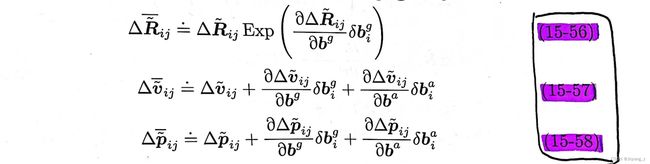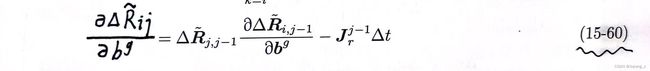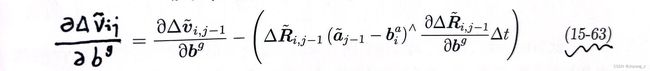IMU-Odom 运动模型

前言：

IMU里程计和视觉里程计、激光里程计等一样，都可以独立计算里程计信息。求解IMU里程计的步骤可以简单的分为三个模块：IMU运动积分、IMU预积分、IMU初始化。

求解IMU里程计的流程参考自ORB：SLAM3。

IMU运动积分

IMU的运动积分公式如下：

由公式可以看出 ：当前时刻的R、V、P都是在上一时刻的R、V、P的基础上推导过来的，且模型中含有向量重力g。

为了使用一段时间的相对量来代替某个时刻的绝对量，且保留重力的影响，于是定义了预积分。 

在求完预积分之后，为了消除预积分中重力的影响，于是进行了IMU初始化求解重力信息。

所以，IMU运动积分可以分解为两个部分：IMU预积分和IMU初始化。

IMU预积分

IMU预积分相对于IMU运动积分的特点是:

1、消除了第i时刻对积分的影响。

2、保留重力的影响。

IMU预积分的公式如下：

预积分中的噪声分离

由于并不知道每个时刻具体的噪声，所以上面的预积分公式中的噪声无法得知，因此无法直接用上面的预积分公式，所以需要进行预积分中的噪声分离工作。

定义预积分的噪声为：

噪声分离后的预积分模型为：

预积分理想值 = 预积分测量值 - 噪声

预积分测量值

噪声目前暂时无法得知，所以预积分理想值也就无法直接求出，但是可以先计算出预积分测量值。预积分测量值的计算公式如下：（也就是预积分模型去掉噪声项）

 ORB-SLAM3中对应的代码：

#Preintegrated::IntegrateNewMeasurement函数中

    // 考虑偏置后的加速度、角速度
    Eigen::Vector3f acc, accW;
    acc << acceleration(0) - b.bax, acceleration(1) - b.bay, acceleration(2) - b.baz;
    accW << angVel(0) - b.bwx, angVel(1) - b.bwy, angVel(2) - b.bwz;


    // Update delta position dP and velocity dV (rely on no-updated delta rotation)
    // 根据没有更新的dR来更新dP与dV  eq.(38)  //note:这里更新顺序为 dP dV dR 不能更换顺序
    dP = dP + dV * dt + 0.5f * dR * acc * dt * dt;
    dV = dV + dR * acc * dt;

    IntegratedRotation dRi(angVel, b, dt);
    // 强行归一化使其符合旋转矩阵的格式 当前时刻的R
    dR = NormalizeRotation(dR * dRi.deltaR); 

根据公式可知，计算顺序为：dP、dV、dR，顺序不可改变。

噪声的递推模型

预积分测量值求得之后就要计算噪声项了，噪声的递推模型如下：

ORB-SLAM3对应的代码： 

/**
 * @brief 预积分计算，更新noise
 * 
 * @param[in] acceleration  加速度计数据
 * @param[in] angVel        陀螺仪数据
 * @param[in] dt            两图像 帧之间时间差
 */
void Preintegrated::IntegrateNewMeasurement(const Eigen::Vector3f &acceleration, const Eigen::Vector3f &angVel, const float &dt)
{
    // 保存imu数据，利用中值积分的结果构造一个预积分类保存在mvMeasurements中
    mvMeasurements.push_back(integrable(acceleration, angVel, dt));

    // Position is updated firstly, as it depends on previously computed velocity and rotation.
    // Velocity is updated secondly, as it depends on previously computed rotation.
    // Rotation is the last to be updated.

    // Matrices to compute covariance
    // Step 1.构造协方差矩阵
    // 噪声矩阵的传递矩阵，这部分用于计算i到j-1历史噪声或者协方差
    Eigen::Matrix A;
    A.setIdentity();
    // 噪声矩阵的传递矩阵，这部分用于计算j-1新的噪声或协方差，这两个矩阵里面的数都是当前时刻的，计算主要是为了下一时刻使用
    Eigen::Matrix B;
    B.setZero();

    // 考虑偏置后的加速度、角速度
    Eigen::Vector3f acc, accW;
    acc << acceleration(0) - b.bax, acceleration(1) - b.bay, acceleration(2) - b.baz;
    accW << angVel(0) - b.bwx, angVel(1) - b.bwy, angVel(2) - b.bwz;

    // 记录平均加速度和角速度
    avgA = (dT * avgA + dR * acc * dt) / (dT + dt);
    avgW = (dT * avgW + accW * dt) / (dT + dt);

    // Update delta position dP and velocity dV (rely on no-updated delta rotation)
    // 根据没有更新的dR来更新dP与dV  eq.(38)  //note:这里更新顺序为 dP dV dR 不能更换顺序
    dP = dP + dV * dt + 0.5f * dR * acc * dt * dt;
    dV = dV + dR * acc * dt;

    // Compute velocity and position parts of matrices A and B (rely on non-updated delta rotation)
    // 根据η_ij = A * η_i,j-1 + B_j-1 * η_j-1中的Ａ矩阵和Ｂ矩阵对速度和位移进行更新
    // note:推导公式在P359-360
    Eigen::Matrix Wacc = Sophus::SO3f::hat(acc);

    A.block<3, 3>(3, 0) = -dR * dt * Wacc;       
    A.block<3, 3>(6, 0) = -0.5f * dR * dt * dt * Wacc;
    A.block<3, 3>(6, 3) = Eigen::DiagonalMatrix(dt, dt, dt);
    B.block<3, 3>(3, 3) = dR * dt;
    B.block<3, 3>(6, 3) = 0.5f * dR * dt * dt;

    // Update position and velocity jacobians wrt bias correction
    // 因为随着时间推移，不可能每次都重新计算雅克比矩阵，所以需要做J(k+1) = j(k) + (~)这类事，分解方式与AB矩阵相同
    // 论文作者对forster论文公式的基础上做了变形，然后递归更新，参见 https://github.com/UZ-SLAMLab/ORB_SLAM3/issues/212
    // note:零偏更新后用，推导公式P361-364
    JPa = JPa + JVa * dt - 0.5f * dR * dt * dt;
    JPg = JPg + JVg * dt - 0.5f * dR * dt * dt * Wacc * JRg;
    JVa = JVa - dR * dt;
    JVg = JVg - dR * dt * Wacc * JRg;

    // Update delta rotation
    // Step 2. 构造函数，会根据更新后的bias进行角度积分
    IntegratedRotation dRi(angVel, b, dt);
    // 强行归一化使其符合旋转矩阵的格式 当前时刻的R
    dR = NormalizeRotation(dR * dRi.deltaR); 

    // Compute rotation parts of matrices A and B
    // 补充AB矩阵
    A.block<3, 3>(0, 0) = dRi.deltaR.transpose();
    B.block<3, 3>(0, 0) = dRi.rightJ * dt;

    // 小量delta初始为0，更新后通常也为0，故省略了小量的更新
    // Update covariance
    // Step 3.更新协方差，frost经典预积分论文的第63个公式，推导了噪声（ηa, ηg）对dR dV dP 的影响
    C.block<9, 9>(0, 0) = A * C.block<9, 9>(0, 0) * A.transpose() + B * Nga * B.transpose();  // B矩阵为9*6矩阵 Nga 6*6对角矩阵，3个陀螺仪噪声的平方，3个加速度计噪声的平方
    // 这一部分最开始是0矩阵，随着积分次数增加，每次都加上随机游走，偏置的信息矩阵
    C.block<6, 6>(9, 9) += NgaWalk;

    // Update rotation jacobian wrt bias correction
    // 计算偏置的雅克比矩阵，r对bg的导数，∂ΔRij/∂bg = (ΔRjj-1) * ∂ΔRij-1/∂bg - Jr(j-1)*t
    // 论文作者对forster论文公式的基础上做了变形，然后递归更新，参见 https://github.com/UZ-SLAMLab/ORB_SLAM3/issues/212
    // ? 为什么先更新JPa、JPg、JVa、JVg最后更新JRg? 答：这里必须先更新dRi才能更新到这个值，但是为什么JPg和JVg依赖的上一个JRg值进行更新的？
    JRg = dRi.deltaR.transpose() * JRg - dRi.rightJ * dt;

    // Total integrated time
    // 更新总时间
    dT += dt;
}

 预积分中零偏更新的影响

在前面所有的预积分模型中，我们都假设第i时刻加速度计和陀螺仪的零偏是固定的，但实际上零偏作为优化变量是不断更新的，如果每次零偏更新后都需要重新计算预积分，那计算代价太大了。

因此我们采用一种简化的思路，假设预积分观测值是随零偏线性变化的，这样可以用预积分观测值关于零偏变化的一阶项来近似更新预积分测量值。计算公式如下：

预积分测量更新值 = 预积分测量值 + 更新值

旋转预积分测量值对零偏的偏导：

速度预积分测量值对零偏的偏导：

位移预积分测量值对零偏的偏导：

ORB-SLAM3对应的代码： 

    // Update position and velocity jacobians wrt bias correction
    // 因为随着时间推移，不可能每次都重新计算雅克比矩阵，所以需要做J(k+1) = j(k) + (~)这类事，分解方式与AB矩阵相同
    // 论文作者对forster论文公式的基础上做了变形，然后递归更新，参见 https://github.com/UZ-SLAMLab/ORB_SLAM3/issues/212
    // note:零偏更新后用，推导公式P361-364
    JPa = JPa + JVa * dt - 0.5f * dR * dt * dt;
    JPg = JPg + JVg * dt - 0.5f * dR * dt * dt * Wacc * JRg;
    JVa = JVa - dR * dt;
    JVg = JVg - dR * dt * Wacc * JRg;

    JRg = dRi.deltaR.transpose() * JRg - dRi.rightJ * dt;

/** 
 * @brief 根据新的偏置计算新的dR
 * @param b_ 新的偏置
 * @return dR    P361
 */
Eigen::Matrix3f Preintegrated::GetDeltaRotation(const Bias &b_)
{
    std::unique_lock lock(mMutex);
    // 计算偏置的变化量
    Eigen::Vector3f dbg;
    dbg << b_.bwx - b.bwx, b_.bwy - b.bwy, b_.bwz - b.bwz;
    // 考虑偏置后，dR对偏置线性化的近似求解,邱笑晨《预积分总结与公式推导》P13～P14
    // Forster论文公式（44）yP17也有结果（但没有推导），后面两个函数GetDeltaPosition和GetDeltaPosition也是基于此推导的
    return NormalizeRotation(dR * Sophus::SO3f::exp(JRg * dbg).matrix());
}

/** 
 * @brief 根据新的偏置计算新的dV
 * @param b_ 新的偏置
 * @return dV   P361
 */
Eigen::Vector3f Preintegrated::GetDeltaVelocity(const Bias &b_)
{
    std::unique_lock lock(mMutex);
    Eigen::Vector3f dbg, dba;
    dbg << b_.bwx - b.bwx, b_.bwy - b.bwy, b_.bwz - b.bwz;
    dba << b_.bax - b.bax, b_.bay - b.bay, b_.baz - b.baz;
    // 考虑偏置后，dV对偏置线性化的近似求解,邱笑晨《预积分总结与公式推导》P13，JPg和JPa在预积分处理中更新 
    return dV + JVg * dbg + JVa * dba;
}

/** 
 * @brief 根据新的偏置计算新的dP
 * @param b_ 新的偏置
 * @return dP
 * @index 对应P361
 */
Eigen::Vector3f Preintegrated::GetDeltaPosition(const Bias &b_)
{
    std::unique_lock lock(mMutex);
    Eigen::Vector3f dbg, dba;
    dbg << b_.bwx - b.bwx, b_.bwy - b.bwy, b_.bwz - b.bwz;
    dba << b_.bax - b.bax, b_.bay - b.bay, b_.baz - b.baz;
    // 考虑偏置后，dP对偏置线性化的近似求解,邱笑晨《预积分总结与公式推导》P13，JPg和JPa在预积分处理中更新
    return dP + JPg * dbg + JPa * dba;
}

---

待更新