MATLAB实现二阶模糊逻辑控制系统仿真

1. 内容

假设某一工业过程可等效成以下二阶系统：

设计一个模糊控制器，使其能自动建立模糊规则库，保证控制规则如表1所示，这种规则可表示为：

式中，fix为取整函数；E为误差的模糊集；DE为误差导数的模糊集；α为常数。

表1 模糊控制规则

u     e de	NB	NS	ZR	PS	PB
NB	PB	PB	PS	PS	ZR
NS	PB	PS	PS	ZR	ZR
ZR	PS	PS	ZR	ZR	NS
PS	PS	ZR	ZR	NS	NS
PB	ZR	ZR	NS	NS	NB

这样表示的模糊控制系统可以通过改变α值方便地修改如表1所示的模糊控制规则，从而自动建立系统的模糊规则库。
要求：

设计模糊控制器，使其能自动建立模糊规则库，保证系统输出尽快跟随系统输入。

要求建立脚本实现上述模糊逻辑控制系统。采样时间T=0.01秒；系统输入r(t)=1.0。观察不同α

取值时，阶跃响应的变化情况，找到匹配较佳动态性能的α

值，并进行详细的实验分析。

2. 过程

脚本：

clear all;
%被控系统建模
num=20;den=[8 6 1];
[A,b,c,d]=tf2ss(num,den);
%系统参数
T=0.01;h=T;
N=500;R=1.0*ones(1,N);
uu=zeros(1,N); yy=zeros(3,N);
ka=1;
for alpha=[0.45 0.75 0.90];
%定义输入/输出变量及其隶属度函数

fisMat=newfis('n4');
fisMat=addvar(fisMat,'input','e',[-6,6]);
fisMat=addvar(fisMat,'input','de',[-6,6]);
fisMat=addvar(fisMat,'output','u',[-6,6]);
fisMat=addmf(fisMat,'input',1, 'NB','trapmf',[-6 -6 -5 -3]);
fisMat=addmf(fisMat,'input',1,'NS','trapmf',[-5 -3 -2 0]);
fisMat=addmf(fisMat,'input',1,'ZR','trimf',[-2 0 2]);
fisMat=addmf(fisMat,'input',1,'PS','trapmf',[0 2 3 5]);
fisMat=addmf(fisMat,'input',1,'PB','trapmf',[3 5 6 6]);
fisMat=addmf(fisMat,'input',2,'NB','trapmf',[-6 -6 -5 -3]);
fisMat=addmf(fisMat,'input',2,'NS','trapmf',[-5 -3 -2 0]);
fisMat=addmf(fisMat,'input',2,'ZR','trimf',[-2 0 2]);
fisMat= addmf(fisMat,'input',2,'PS','trapmf',[0 2 3 5]);
fisMat=addmf(fisMat,'input',2,'PB','trapmf',[3 5 6 6]);
fisMat=addmf(fisMat,'output',1,'NB','trapmf',[-6 -6 -5 -3]);
fisMat=addmf(fisMat,'output',1,'NS','trapmf',[-5 -3 -2 0]);
fisMat=addmf(fisMat,'output',1,'ZR','trimf',[-2 0 2]);
fisMat=addmf(fisMat,'output',1,'PS','trapmf',[0 2 3 5]);
fisMat=addmf(fisMat,'output',1,'PB','trapmf',[3 5 6 6]);
%模糊规则矩阵
for i=1:5
         for j=1:5
                   rr(i,j)=round(alpha*i+(1-alpha)*j);
         end
end
rr=6-rr;
r1=zeros(prod(size(rr)),3);
k=1;
for i=1:size(rr,1)
         for j=1:size(rr,2)
                   r1(k,:)=[i,j,rr(i,j)];
                   k=k+1;
        end
end
[r,s]=size(r1);
r2=ones(r,2);
rulelist=[r1 r2];
fisMat=addrule(fisMat,rulelist);
%模糊控制系统仿真
Ke=30;Kd=0.2;
Ku=1.0;x=[0;0];
e=0;de=0;
for k=1:N
           e1=Ke*e;
           de1=Kd*de;
%将模糊控制器的输入变量变换到论域
      if e1>=6
             e1=6;
      elseif e1<=-6
             e1=-6;
      end
      if de1>=6;
            de1=6;
      elseif de1<=-6
             de1=-6;
      end
%计算模糊控制器的输出
      in=[e1 de1];
      uu(1,k)=Ku*evalfis(in,fisMat);
      u=uu(1,k);
      %利用四阶龙格-库塔法计算系统输出
      K1=A*x+b*u;
      K2=A*(x+h*K1/2)+b*u;
      K3=A*(x+h*K2/2)+b*u;
      K4=A*(x+h*K3)+b*u;
      x=x+(K1+2*K2+2*K3+K4)*h/6;
      y=c*x+d*u;
      yy(ka,k)=y;
%计算误差和误差微分
      e1=e;e=y-R(1,k);
      de=(e-e1)/T;
    end
    ka=ka+1;
end
%绘制结果曲线
kk=[1:N]*T;
plot(kk,yy(1,:),'r:',kk,yy(2,:),'r-.',kk,yy(3,:),'k--',kk,R,'m');
xlabel('时间');ylabel('输出');
legend('alpha=0.45','alpha=0.75','alpha=0.90');
grid on;

初始num：20

模糊系统中参数初始值：Ke=30，Kd=0.2，Ku=1.0

运行结果：

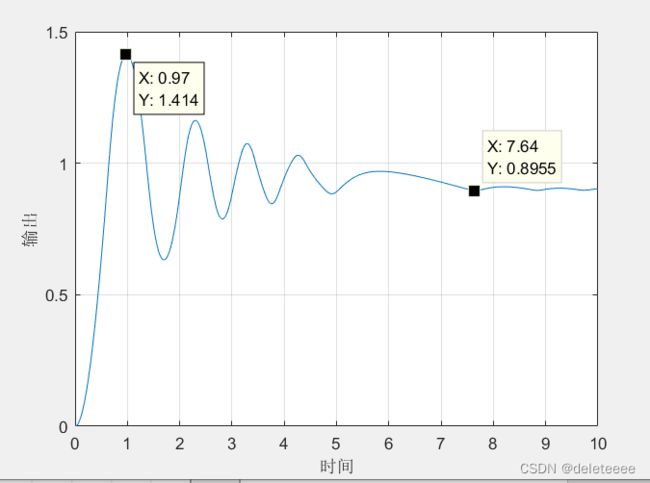
图1 alpha为0.45，0.75，0.90时的系统阶跃响应曲线

接下来修改alpha的值来进行探究：

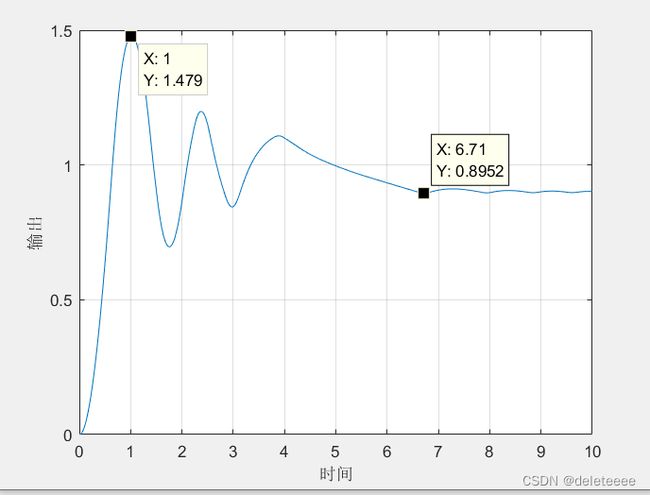
图2 alpha=1

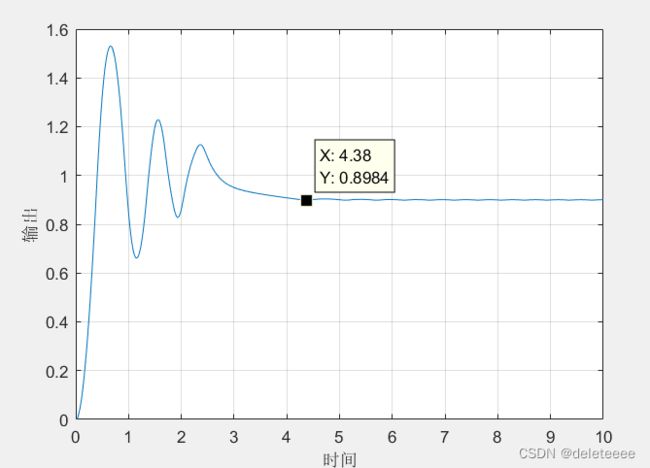
图3 alpha=0.5

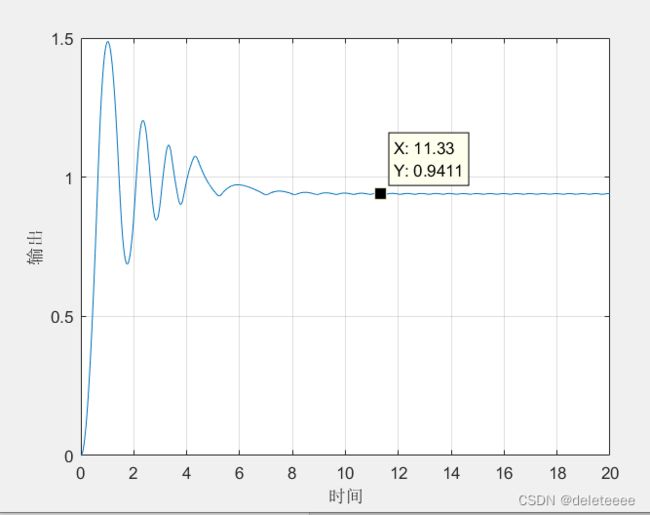
图4 alpha=0.3

图5 alpha=0.3 开环增益（num值）为50

图6 alpha=0.3，num=20，模糊系统中Ke=50

图7 alpha=0.3，num=20，模糊系统中Ke=50，Ku=10

图8 alpha=0.3，num=20，模糊系统中Ke=100，Ku=10

图9 alpha=0.3，num=20，模糊系统中Ke=100，Ku=10，Kd=0.8

图10 alpha=0.3，num=20，模糊系统中Ke=50，Ku=10，Kd=1

图11 alpha=0.25

图12 alpha=0.251

3. 分析

从图1中我们可以看出，alpha为0.9的时候超调量最大，但是调节时间也相对较大，而为0.45的时候调节时间较小。在alpha值增加至1如图2时，与图1中0.9的曲线基本一致，继续减小alpha的值，如图3，图4所示，随着值的减小，调节时间也在减小，振荡频率在降低，但是稳态误差始终没有降低，所以在alpha值减小值0.3后，我开始改变其它参数，首先改变了开环增益num的值，如图5所示，调节时间略有减小，但是稳态误差还是没有变化，然后我开始考虑模糊系统中的Ke，Kd，Ku这三个参数的调节，首先增大Ke值，如图6所示，稳态误差终于减小了，但是同时系统超调也有增加，再增大Ku的值为1，图7所示曲线上升时间加快，振荡频率加大，但是稳态误差没有改变，此时若继续增大Ke值为100，图8所示曲线稳态误差继续减小，超调也会增加，保持此时的状态，我开始逐渐再增加Kd的值，如图9和图10所示，系统超调减小，但是响应时间增加了。将参数恢复初始状态，当alpha值减小到0.25后，如图11所示曲线先上升然后一直下降趋向于0，但是我将alpha调整为0.251如图12时，曲线还接近alpha为0.3时的曲线，也就是说alpha在0.25的时候会有一次较大的改变。综上所述，我们可以推测，Ke变大缩短上升时间，但是增大系统超调。Kd变大减小系统超调，但是响应速率变慢。Ku过小，系统的动态响应过程变长，Ku过大会导致系统震荡。我们需要综合调整以上三个因子，获得所需要的控制性能。