数据结构——复杂度讲解(2)
作者:几冬雪来
时间:2023年2月22日
内容:数据结构复杂度讲解
目录
前言:
复杂度讲解(2):
1.空间复杂度是什么:
2.空间复杂度讲解:
结尾:
前言:
在这之前我们写了一篇博客,内容是对我们的数据结构的复杂度进行了一个初步的讲解,并通过了几道题对我们的知识进行了巩固。但是我们的数据结构的复杂度讲解并没有就此结束,今天我们将对我们的数据结构的复杂度进行进一步的分析说明。
复杂度讲解(2):
在我们上一篇的数据结构的讲解中,我们对我们复杂度中的时间复杂度进行了一个大致的说明,但是我们也说过,我们的时间复杂度只是我们算法效率的其中一个复杂度,因此今天我们将对另一个复杂度——空间复杂度进行讲解。
1.空间复杂度是什么:
在上一篇博客我们讲到,要衡量我们算法的效率可以从时间和空间两个维度进行讲解,时间复杂度是我们的代码大概运行的次数,那么我们的另一个维度,空间复杂度是什么呢?在我们的数据结构中,我们的空间复杂度也是一个数学表达式。它是对一个算法在运行过程中临时占用存储空间大小的量度。
它在这里并不是计算我们的字节大小,而是计算变量的个数。 其次我们的空间复杂度的计算也是使用我们的大O的渐进表示法。它和我们时间复杂度的计算原理十分相似。
2.空间复杂度讲解:
我们依旧写题进行举例,来计算我们的空间复杂度。就例如我们下面这个冒泡排序的空间复杂度的计算。
但是对于我们这个代码的空间复杂度出现了两种不一样的看法。
有点人认为我们这里创造了3个临时变量,有人则认为我们这里的临时变量要更多,那是为什么呢? 首先是我们的最明显的三个临时变量,这个大家应该都是没有争议的。
到这里有人就下结论了,我们这里的变量的个数是一个常数,因此我们这里的空间复杂度应该被写为O(1)。但是有人就有不一样的看法,有人就看到了我们这个代码的参数,我们这里使用传址调用传递了我们一个数组的地址,而我们的数组中有n个值,所以我们这里的空间复杂度应该是O(N)。
那么这里就引申了一个问题,在我们的这个冒泡排序中,到底有没有计算我们这个数组的空间?
这里就要结合我们上面的定义,这里我们的数组并不是为了计算我们的数组所创建的,它是我们数据源的提供。因为我们要对我们的数组进行冒泡排序,所以我们才引进了这一个数组,所以我们这里数组的个数并未算入其中,所以我们这里就只创造了三个临时变量,我们的空间复杂度为O(1)。
那么搞懂了这道题之后,接下来我们再写一道题。
这是我们的斐波那契函数,不同的是,这里我们并不是计算我们数组第n项的值,而是计算我们的前n项。 所以这里我们通过我们的malloc函数开辟了一块n+1大小的空间,而且这里我们的这块数组和我们的冒泡排序的题不一样,这里是为了计算我们的斐波那契前n项所额外开辟的一个数组,因此我们这个代码的空间复杂度是O(N)。
通过这两个代码,其实我们可以看出我们的空间复杂度并没有时间复杂度那么复杂。
接下来我们再做几道题目来巩固一下知识。
在上面上面求出了冒泡排序和斐波那契函数的空间复杂度,那么接下来我们就再来求一求我们递归函数的空间复杂度。
这里我们如果简单来看,我们这个函数并没有建立什么临时变量,因此我们的空间复杂度是O(1)。 但是其实这里我们运用到了递归的知识,而递归则要建立栈帧。而在这里,我们要建立N+1层栈帧。
这里我们就累计创建了N+1层栈帧,所以我们的空间复杂度是O(N)。这是为了运行我们的算法所而外开辟的空间。
下来我们再看一道题。
这道题我们之前讲过它的时间复杂度,我们这个代码的时间复杂度是O(2^N)。 你瞒我瞒这个代码的空间复杂度也是O(2^N)吗?其实不是,我们这个代码的空间复杂度其实是O(N)。为什么?这里就涉及一个问题,递归调用是怎么样调用的?
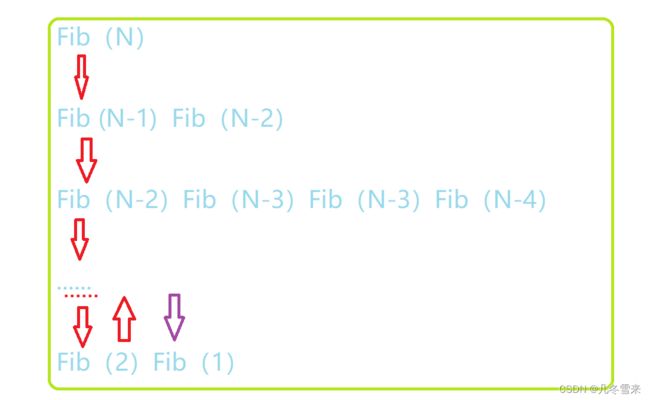
这里我们斐波那契函数从N开始,一开始我们调用的是N-1,接下来我们并不是调用同一行的N-2,我们是会继续往下执行,调用我们下方的N-2。 当我们最左边的斐波那契函数调用到不能再调用的时候我们就往回返回,接下来我们才继续往右边继续调用。
而且在这里我们的第一次调用结束的Fib(2)和我们返回后再次向下调用的Fib(1)是同一块空间。
这里就是我们的大概的运行过程。这里我们通过对比时间复杂度和空间复杂度也可以知道一个道理。
时间一去不复返,不可以重复利用
空间用了之后归还,可以重复利用
到这里,除了一部分比较复杂的空间复杂度,我们的空间复杂度到这里就基本讲解完了。通过以上用例,我们可以看出对比起我们的时间维度,我们的空间维度的例题讲解就相对较少。但是从我们后面的两道题目的讲解来看,我们算法效率的空间复杂度并不是那么简单的。最后一题如果没有进行讲解的话,可能大部分人都会掉到坑里,大多数人以为空间销毁就是指这块空间消失了,其实我们空间的销毁实际上可以理解为是将我们这块空间的使用权还给我们的操作系统。
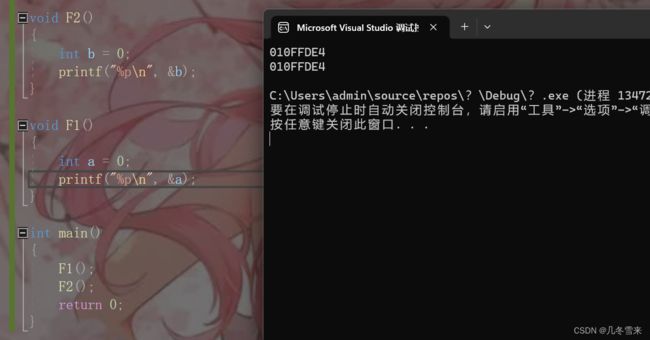
类似我们的这个代码,就能大概解释我们上面的两道题。
在我们这里一开始我们就调用了F1,调用完了F1之后,我们这里没有后续的操作,那么我们这里的F1运行结束,结束完了之后我们的栈帧就要进行销毁,空间销毁可以说是我们把使用权还给操作系统。 接下来我们要调用F2,因为在F1调用之后,我们将这块空间还给了操作系统,所以在创建F2的时候,我们又要向操作系统申请空间。这里操作系统就会给我们开辟一块空间命名为F2,在F2中我们又定义一个变量为b,因为我们的a和b执行的指令和内容基本一致,因此我们这块空间又被取了一个b的名字,这就导致了我们这里a和b的地址是一样的。
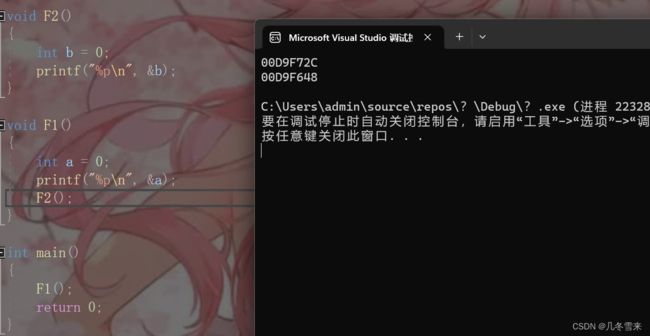
如果这里我们不想让它们共用同一块空间,和上面的代码不一样,在上面那个代码中,我们是调用完了F1之后再调用F2,而在这个代码中,我们是先调用F1,然后再在F1中调用F2,这是一种链式调用。
在我们第一种代码中的F1或者F2中多几个变量,也可能导致地址不一样。
结尾:
这篇博客基本将我们的数据结构的时间复杂度和空间复杂度都讲解完了,但是这并不意味着我们的算法效率那部分内容到这里就彻彻底底的结束了,在我们后面学习其他内容又或者是写题的时候,有的时候我们或多或少也会再次接触到我们的时间和空间复杂度,这篇博客是我返校上课的第一篇博客,可能是我个人没有适应学校的这种环境,导致我感觉自己写的博客有点乱,后面我会调整一下自己,希望这篇博客对大家能有所帮助。