详解C++如何取随机数以及处理各种随机问题
文章目录
- C++取均匀随机数的方法
-
- 1、c语言中简单的rand()--范围有限0~32767
- 2、mt19937方法--范围无限
- C++关于均匀随机数的应用
-
- 1、在圆内随机生成点(取值范围不是条形)
- 2、非重叠矩阵中的随机点(找准取值范围)
- C++带权重的随机选择算法(取值范围变形)
-
- 前缀和+二分搜索搞定取值范围变形
- 对于左右都闭的二分搜索,选择最左还是最右的技巧
- 对于lower_bound和upper_bound的区别
- C++常数时间删除/查找数组中的任意元素
-
- 1、数组的常数时间删除并随机返回元素
- 2、黑名单的随机数(不能像圆内随机那样,重复调用随机函数)
-
- 前缀和+二分查找
- 哈希映射
- C++在无限序列中随机抽取元素
-
- 水塘抽样算法
- 1、 链表随机节点
- 2、随机数索引
-
- 哈希秒杀
- 水塘抽样---超时了竟然
C++取均匀随机数的方法
1、c语言中简单的rand()–范围有限0~32767
对于题目中取值范围小的可用rand(),省去了各类定义的麻烦
其用法为:随机取[n,m)之间的数,其调用方法为:rand()%(m-n+1) + n
int ans = rand() % 5 +1; //范围指从1开始有5个--1,2,3,4,5
int ans = rand() %5;//范围指从0开始有5个--0,1,2,3,4
2、mt19937方法–范围无限
1、随机数发生器。mt指的是Mersenne Twister算法,是伪随机数发生器之一,其主要作用是生成伪随机数。而19937是因为其产生随机数的速度快、周期长,范围能到2^19937-1。其用法与rand()函数类似。
2、随机数发生器的种子。现有的随机数函数都存在一个问题:在利用循环多次获取随机数时,如果程序运行过快或者使用了多线程等方法,容易使种子重复从而随机数重复。因此可以利用C++11中的真随机数发生器产生的数做种子—random_device。(不直接用它是因为他的速度很慢)
3、取数器。rand()是用%来框定随机的取值范围,而mt19937需要搭配一个专门的函数来限定取随机数的范围:
//题目中均匀随机的要求可就是从这里实现的.注意real是浮点数,而int是整型
template <class IntType = int> class uniform_int_distribution(a,b);
template <class IntType = double> class uniform_real_distribution(a,b);//想0-1取概论就从这里出发
他会根据发生器,以均匀的概率产生a到b之间的数[a,b],这是闭区间!
因此,组合在一起就是一下模板:
mt19937 gen{random_device{}()};//声明:产生器+种子。
//--上面这俩需要#includeC++关于均匀随机数的应用
1、在圆内随机生成点(取值范围不是条形)
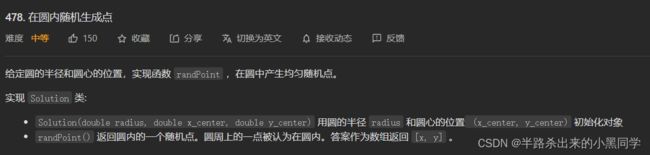
从上面我们所写的随机数模板也可以知道,产生的随机数都是一个条形的范围,那么如果使其变为圆形呢,其实完全可以取两个条形的范围组成一个矩形的范围,然后再加个判断,当去到圆外时,就重新取即可!
class Solution {
private:
mt19937 gen{random_device{}()};
uniform_real_distribution<double> dis;
//无法直接就定义好,需在调用函数时,在函数体的冒号初始化下,进行括号赋予范围!
double xc, yc, r;
public:
Solution(double radius, double x_center, double y_center): dis(-radius, radius), xc(x_center), yc(y_center), r(radius) {}
vector<double> randPoint() {
//靠这个wile(true)来不断尝试,直至随机出圆内的点再返回
while (true) {
double x = dis(gen), y = dis(gen);
if (x * x + y * y <= r * r) {
return {xc + x, yc + y};
}
}
}
};
2、非重叠矩阵中的随机点(找准取值范围)


其核心是随机所有点,因此创造均匀分布的数的范围应该是所有矩形覆盖的整数点(即把所有矩形都拆成一个个像素组成的条,就是个降维的操作,二向箔嘿嘿~)。其计算公式就是(x-a+1)*(y-b+1)
而一个矩形中的所有像素点的相对坐标为(必背):
//当前点在这个矩形中的相对左下角的相对坐标
int x = idx%rowPoints;
int y = idx/rowPoints;
本质就是前缀和解决,只不过由随机数找前缀和的过程是用二分法的!!!但是,二分查找记得要用右对齐的right_bound二分查找来找到正好比其少的地方,随后+1就是该随机到的像素点,所在的矩阵情况。
【原因】当目标元素 target 不存在数组 nums 中时,搜索左侧边界的二分搜索的返回值可以做以下几种解读:
1、返回的这个值是 nums 中大于等于 target 的最小元素索引。
2、返回的这个值是 target 应该插入在 nums 中的索引位置。
3、返回的这个值是 nums 中小于 target 的元素个数。
比如在有序数组 nums = [2,3,5,7] 中搜索 target = 4,搜索左边界的二分算法会返回 2(也就是指向5),你带入上面的说法,都是对的。而搜索右边界的二分算法就会返回1(也就是指向3)。
【技巧】随机数取 [1, sum[w]] 对应找左边界,如果 [0, sum[w] - 1] 会使最左边多占一份,而最右边少占一份;
随机数取 [0, sum[w] - 1] 对应找右边界+1,如果 [1, sum[w]] 会使最左边少占一份,最右索引溢出。
class Solution {
public:
int n=0;
vector<int> sum_point;//前缀和
mt19937 gen{random_device{}()};
vector<vector<int>>rects;
Solution(vector<vector<int>>& rects): rects{rects} {
n = rects.size();
sum_point.resize(n,0);
//baseline可前万别忘了~!
sum_point[0] = (rects[0][2] - rects[0][0] + 1) * (rects[0][3] - rects[0][1] + 1);
for(int i=1;i<n;++i)
{
int length = rects[i][2]-rects[i][0]+1;
int height = rects[i][3]-rects[i][1]+1;
sum_point[i] = height*length+sum_point[i-1];
}
}
vector<int> pick() {
uniform_int_distribution<int> dis_point(0,sum_point[n-1]-1);
int point = dis_point(gen);
int lp=0,rp=n-1;
while(lp<=rp)
{
int mid = lp+(rp-lp)/2;
if(sum_point[mid]>point) rp=mid-1;
else lp = mid+1;
}
int num = rp+1;
if (num > 0) point -= sum_point[num-1];
int length = rects[num][2]-rects[num][0]+1;
int x = point % length;
int y = point / length;
return{rects[num][0]+x,rects[num][1]+y};
}
};
C++带权重的随机选择算法(取值范围变形)
前缀和+二分搜索搞定取值范围变形
有了上节的第2题,其实我们可以用相同的方法,把这类带权重的化成均匀抽取的,例如下面的W=[1,3]例子,我们就可以看作是在[0,1,1,1]上均匀抽取。因此方法依旧是老样子,前缀和+二分搜索,具体可分为以下几步:
1、根据权重生成前缀和数组
2、生成一个在前缀和数组内的随机数
3、通过二分搜索的左侧边界搜索(原因上面也提到了)找到这个随机数的最小元素索引。

对于左右都闭的二分搜索,选择最左还是最右的技巧
【技巧】随机数取 [1, sum[w]] 对应找左边界,如果 [0, sum[w] - 1] 会使最左边多占一份,而最右边少占一份;
随机数取 [0, sum[w] - 1] 对应找右边界+1,如果 [1, sum[w]] 会使最左边少占一份,最右索引溢出。
class Solution {
public:
vector<int>add_num;
mt19937 gen{random_device{}()};
Solution(vector<int>& w) {
int tem=0;
for(auto a:w)
{
tem+=a;
add_num.push_back(tem);
}
}
int pickIndex() {
uniform_int_distribution<int> dis(1,add_num.back());
int x = dis(gen);
int lp = 0,rp = add_num.size()-1;
while(lp<=rp)
{
int mid = lp+(rp-lp)/2;
if(add_num[mid]>=x) rp = mid-1;
else lp = mid+1;
}
return lp;
}
};
让我们再用STL函数优化一下:
class Solution {
private:
mt19937 gen{random_device{}()};
uniform_int_distribution<int> dis;
vector<int> add_num;
public:
//accumulate 头文件在中,求特定范围内所有元素的和。
Solution(vector<int>& w):dis(1, accumulate(w.begin(), w.end(), 0)) {
partial_sum(w.begin(), w.end(), back_inserter(pre));
//back_inserter函数头文件,用于在末尾插入元素。
}
//spartial_sum函数的头文件在,对(first, last)内的元素逐个求累计和,放在result容器内
int pickIndex() {
int x = dis(gen);
return lower_bound(pre.begin(), pre.end(), x) - pre.begin();
//lower_bound头文件在,用于找出范围内不小于num的第一个元素的迭代器,也是因此,减去.begin()的迭代器就是下标了!妙啊妙啊!!这也是迭代器快速得到下标的一个方法,学到了!
}
};
对于lower_bound和upper_bound的区别
其实一个是大于等于,一个大于,这个的区别:
当目标值存在时,upper_bound-1(要减1哦)就是相当于找最右区间的二分查找的right指针。lower_bound就是相当于找最左区间的二分查找的left指针。
当目标值不存在时,这两个函数的返回值相同,其都是最左区间的二分查找的left指针的效果(指向第一个大于目标值的地方)
C++常数时间删除/查找数组中的任意元素
1、数组的常数时间删除并随机返回元素

1、想要插入和删除元素在线性的时间内,那么就两个数据结构可以做到,一个是哈希表还有一个就是紧凑的数组。而哈希表对于随机取数,由于各种解决哈希冲突的机制,其无法做到O(1)时间随机获取,因此就是用数组。我们就可以直接生成随机数作为索引,从数组中取出该随机索引对应的元素,作为随机元素。
2、那么数组该怎么变紧凑从而实现快速插入删除呢,插入好说,删除的话就只能与尾部进行交换然后pop掉。因此就需要用一个哈希表来记录每个每个元素对应的索引。
class RandomizedSet {
public:
RandomizedSet() {
}
bool insert(int val)
{
if(!record.count(val))
{
record[val] = ans.size();
ans.push_back(val);
return true;
}
else return false;
}
bool remove(int val) {
if(record.count(val))
{
int i = record[val];
record[ans.back()] = i;
swap(ans[i],ans.back());
ans.pop_back();
record.erase(val);
return true;
}
else return false;
}
int getRandom() {
uniform_int_distribution<int>dis(0,ans.size()-1);
int x = dis(gen);
return ans[x];
}
private:
unordered_map<int,int>record;
vector<int>ans;
mt19937 gen{random_device{}()};
};
2、黑名单的随机数(不能像圆内随机那样,重复调用随机函数)
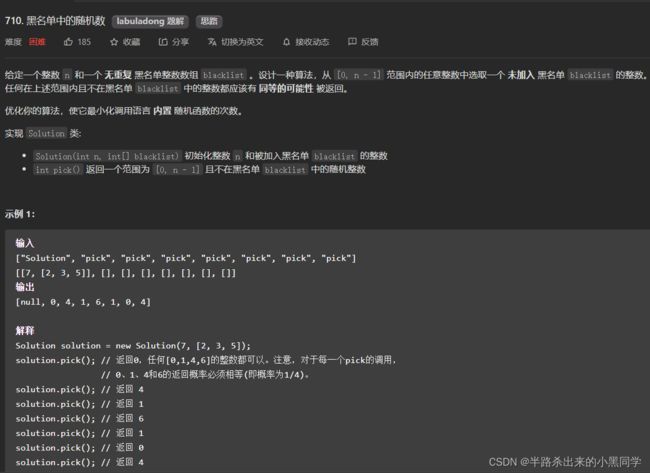
题目中有一句话**优化你的算法,使它最小化调用语言 内置 随机函数的次数。**这句话就简单直接地说明了不能像圆那样,重复调用随机函数。
其实本题有两个解决方法!
前缀和+二分查找
【第一种】仍然是前缀和+二分查找,只要去掉黑名单的数字,依旧是那样
class Solution
{
public:
using T = pair<int, int>;
vector<T> m; // 存放各个区间
vector<int> s; // 存放前缀和, 即m各个区间长度的前缀和
Solution(int n, vector<int>& blacklist)
{
sort(blacklist.begin(), blacklist.end()); // 首先对黑名单区间排序
int b_n = blacklist.size();
int st = 0; // st表示一个新区间的左端点, 默认为0
s.push_back(0);
for(auto v : blacklist)
{
if(v == st) // 若该区间的待加入区间的左端点是黑名单的数则++
{
++st;
continue;
}
m.push_back({st, v - 1}); // 加入一个新区间
s.push_back(s.back() + v - st); // (v - 1) - st + 1 表示该新区间的长度
st = v + 1;
}
// 最后一个区间的加入 st ~ n - 1, 但要注意判断是否可加入
if(st != n)
{
m.push_back({st, n - 1});
s.push_back(s.back() + n - st);
}
}
int pick()
{
int N = s.back();
int t = rand() % N + 1; // 总线段得到一个随机数, 因为区间长度至少为1, 所以需要+1, 从1开始
// 二分查找, 找 t 是落在那个区间上的
int l = 1, r = s.size() - 1;
while(r >= l)
{
int mid = l + r >> 1;
if(s[mid] >= t) r = mid-1;
else l = mid + 1;
}
auto iter = m[l - 1]; // 注意 r - 1, 因为m的区间是从0下标开始存储的
int n = iter.second - iter.first + 1; // 得到本次随机到区间的长度
return iter.first + rand() % n; // 该区间的(左端点数值 + 随机数) 即为最终答案
}
};
哈希映射
可以利用哈希表巧妙处理映射关系,让数组在逻辑上是紧凑的,方便随机取元素。就是把黑名单的数组映射到后n个去,然后把前n个当作白名单,随机取数字的时候,只在前n个里面取就ok了。
class Solution {
public:
Solution(int n, vector<int>& blacklist) {
sort(blacklist.begin(),blacklist.end(),greater<int>());
//先排序,这样防止一次循环不够
int num = blacklist.size();
range = n-num-1;//确定白名单和黑名单的界限
int last = n-1;//从界限从最后开始推
for(auto black:blacklist)
{
if(black>range)//这是黑名单本来就在黑名单区域的情况
{
list_map[black] = black;
continue;
}
//防止黑名单已在的区域占位
while(list_map.count(last)) --last;
list_map[black] = last--;
}
}
int pick() {
uniform_int_distribution<int>dis(0,range);
int x = dis(gen);
//碰到黑名单的,就映射即可
if (list_map.count(x)) return list_map[x];
else return x;
}
private:
unordered_map<int,int>list_map;
mt19937 gen{random_device{}()};
int range;
};
C++在无限序列中随机抽取元素
上面的几个主题,几乎可以通过前缀和和二分查找都搞定,但是对于无线序列,可没有办法通过一个0,n的范围来找去随机数!
让我们回到这个问题,假设一个问题这样:
一个未知长度的链表,请你设计一个算法,只能遍历一次,随机地均匀返回链表中的一个节点。
水塘抽样算法
其实就是动态地进行随机选择,其应该遵循以下规则(可以自行搜索证明过程,是符合数学推理的):
【对于一个一个地动态选择时】当你遇到第 i 个元素时,应该有 1/i 的概率选择该元素,1 - 1/i 的概率保持原有的选择。
【对于多个数一次一次地动态选择时】如果要随机选择 k 个数,只要在第 i 个元素处以 k/i 的概率选择该元素,以 1 - k/i 的概率保持原有选择即可
让我们直接实战操作一下:
1、 链表随机节点
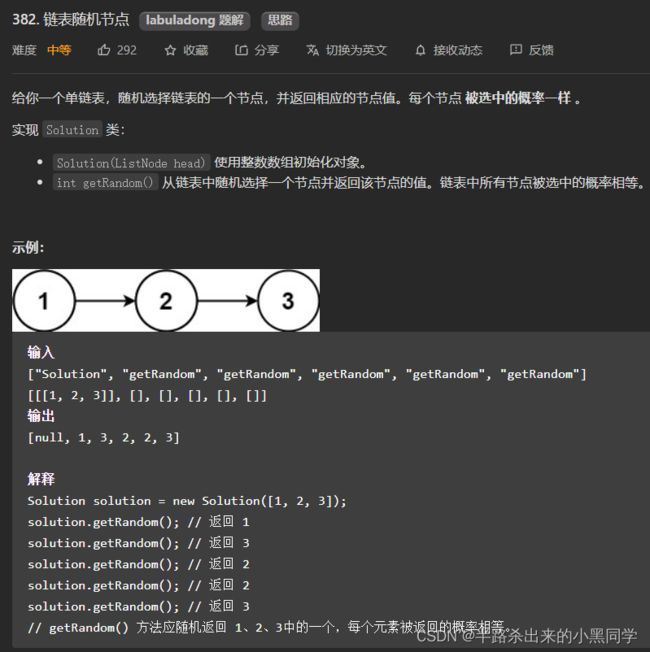
【分析】链表和数组可不一样,一开始时不知道它有多长的,因此我们可以用水塘抽样算法。
class Solution {
public:
Solution(ListNode* head) {
this -> head = head;
}
int getRandom() {
ListNode* root = head;
//注意这里跟head区别开,否则调用一次head永远为空
int ans=0;i=0;
while(root!=nullptr)
{
i++;//注意这个i可是从1开始的,0可没法成为分母
uniform_int_distribution<int>dis(0,i-1);
//因为有0,所以i个是从0~i-1
//由于本题规定val小于10的四次方,其实可以用rand()%i来判断快速解决
if(dis(gen) == 0) ans = root->val;
root = root->next;
}
return ans;
}
private:
mt19937 gen{random_device{}()};
ListNode* head;
int i;
};
2、随机数索引
本题由于1 <= nums.length <= 2 * 10的4次方,小于30000,因此就直接用小范围的rand()偷个懒了。
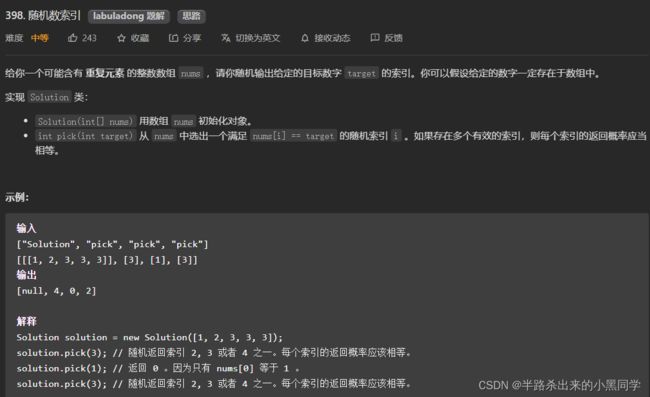
【分析】首先本题可以直接用哈希表来秒杀,一个记录值,另一个数组存放每个值的下标。对于pick,可以直接取出数组,直接随机下标。
哈希秒杀
class Solution {
public:
unordered_map<int,vector<int>> record;
Solution(vector<int>& nums) {
for(int i=0;i<nums.size();++i)
{
record[nums[i]].push_back(i);
}
}
int pick(int target) {
vector<int> ans = record[target];
int n = ans.size();
return ans[rand()%n];//偷个懒其实没问题
}
};
水塘抽样—超时了竟然
这个没啥可说的,只不过等到遍历到nums中等于target的值时再去求概率,竟然超时了,没办法,还是哈希秒杀吧~不过可以学学应用。
class Solution {
public:
vector<int> nums;
Solution(vector<int>& nums) {
this -> nums = nums;
}
int pick(int target) {
int i = 0,ans = 0;
for(int index = 0;index<nums.size();++index)
{
if(nums[index] == target)
{
++i;
if(rand()%i==0) ans = index;
}
}
return ans;
}
};