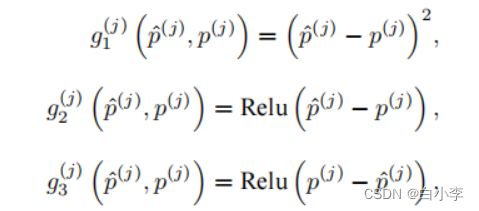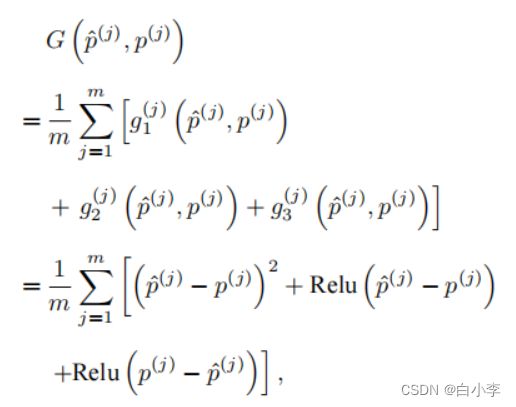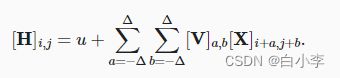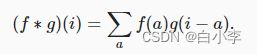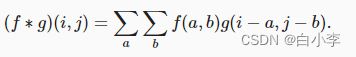对于CNN的文献阅读和识别手写数字的复现

摘要

一、文献阅读

1、题目

2、摘要

3、引言

4、CNN模型结构

5、实验过程

6、同GS算法的对比

二、CNN识别手写数字

1、两个性质

2、图像卷积

总结

---

摘要

在论文方面阅读了基于CNN网络对于大气湍流相位的提取，对CNN的结构网络和运行原理进行了学习，对CNN识别手写数字方面展开了编码，采用MINST数据集进行训练模型，并计划通过窗口就行可视化展现。

I read the paper on phase extraction of atmospheric turbulence based on CNN network, and learned the structure network and working principle of CNN from it. In addition, I encode the recognition of handwritten digits by CNN, and train the model through the MINST dataset.At present，I plan to visualize it through a window.

一、文献阅读

1、题目

基于深度卷积神经网络的大气湍流相位提取

DOI链接：DOI: 10.7498/aps.69.20190982

2、摘要

光束在自由空间中传播时容易受到大气湍流的影响, 其对传输光束的影响相当于附加一个随机噪声相位, 导致传输光束质量下降。本文提出了一种基于深度卷积神经网络 (convolutional neural network, CNN) 的 湍流相位信息提取方法, 该方法采用受湍流影响的光强图为特征提取对象, 经过对海量样本进行自主学习后, CNN 的损失函数值收敛到 0.02 左右, 其在测试集上的平均损失函数值低于 0.03。训练好的 CNN 模型具有很好的泛化能力 , 可以直接根据输入的光强图准确提取出湍流相位。利用 I5-8500CPU, 预测下列三种湍流强度。

这三种湍流强度的湍流相位所需要的平均时间低至5 × 10−3 s 。此外, CNN 的湍流相位提取能力可以通过提高计算能力或者优化模型结构来进一步提升。这些结果表明, 基于 CNN 的湍流相位提取方法能够有效的提取湍流相位, 在湍流补偿、大气湍流特性研究和图像重构等方面具有重要的应用价值。

3、引言

传统的湍流相位提取方法多采用 Gerchberg-Saxton (GS)算法 , Fu 等利用CCD相机采集受大气湍流影响的高斯光束的强度分布, 利用GS算法最终可以得到影响高斯光束的湍流相位。但是, 传统的GS算法无记忆性, 即每次预测都需要重新设置初始相位进行多次迭代, 并且容易出现迭代停滞。另外, 利用随机并行梯度下降算法的自适应光学技术补偿大气湍流效应也是一种可行的方法, 但是随机并行梯度下降算法收敛效果和速度易受增益系数的影响。若增益系数选择不正确易使优化曲线陷入局部极值, 增加了湍流补偿系统的不稳定性。

提出一种基于深度 CNN 的大气湍流湍流提取方法. 利用 CNN 出色的图像处理能力, 将标准高斯光束和受湍流影响的畸变高斯光束共同作为CNN 的输入, 湍流相位作为输出。经过海量样本集的有监督式的训练学习后, 最终可以得到一个具有强泛化能力、能自动提取湍流相位的 CNN 模型。

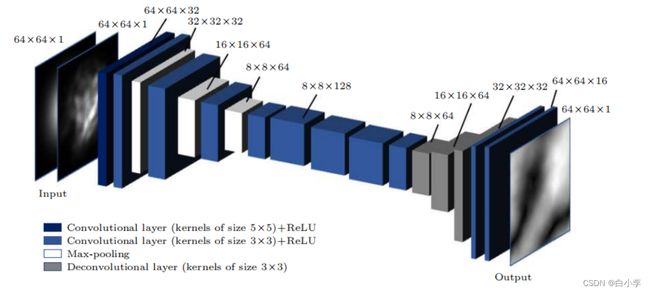
4、CNN模型结构

在此论文中所采用的CNN模型共包含19层模型，输出输入各一层，11层卷积层、3层池化层、3层反卷积层。在输入层中，是两幅单通道的二维图像, 一幅是标准的高斯光束, 另一幅是受大气湍流影响的高斯光束。两幅图像尺寸大小都被缩小到64✖64 。 经过卷积核大小为5✖5的第一层卷积层（Conv1）后得到32个大小为64✖64的特征图；第二层还是卷积层 (Conv2), 通过3✖3的卷积核后得到了 32 个大小为64✖64的特征图; 第三层是池化层 (Pool1), 采用的是最大池化操作, 池化核尺寸为32✖32 , 步长为 2, 非重叠池化, 所以输出特征图尺寸减半, 即此时特征图大小为32✖32 , 但特征图的数量没有变, 仍然是 32 个. 之后再经过两次相同的卷积层和池化层交替设置的结构后, 得到 64 个大小为8✖8的特征图, 再经过 5 层纯粹的卷积层, 所用的卷积核大小都为3✖3。 在第十三层至第十五层添加了反卷积层, 卷积核大小都是3✖3 , 这里设置反卷积层的目的是为了还原湍流相位. 经过三层的反卷积层后再经过 2 层卷积核大小为3✖3的卷积层后就可以得到尺寸大小为64✖64的输出图像。

 这里所用的评估索引为 j 的样本误差损失函数为

对于给定的训练集, 这个误差只与模型的训练参数 (卷积核 和标量偏差b) 有关, 然后再将训练集中所有样本误差的平均来衡量模型预测的质量,即：

其中，m为采集的样本数。

 

5、实验过程

对3三种湍流强度分别设置了70000个训练集，3000个测试集，2600个校验集。训练集用于对CNN模型进行训练,在训练过程中最小化损失函数来不断优化模型参数, 校验集用于将训练过程可视化, 呈现不同训练迭代次数时 CNN 对湍流相位的预测效果. 训练好的 CNN 模型用测试集进行测试, 一个良好的 CNN 模型不仅追求训练误差小, 而且要求测试误差尽可能小。

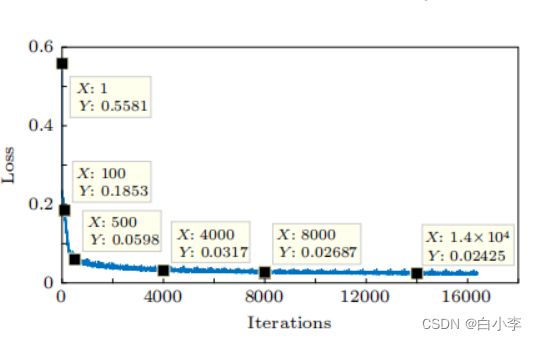
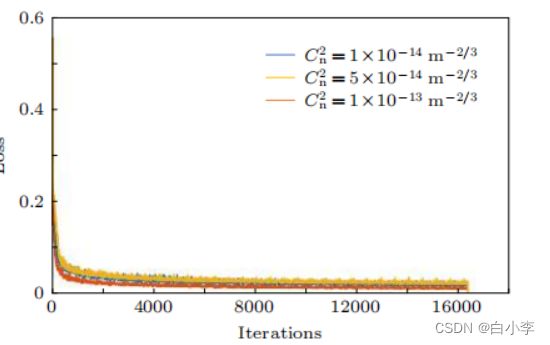
湍流强度为 的训练损失函数的变化曲线如下图所示。

各湍流强度损失函数曲线

 从下图可以看出CNN输出的预测湍流相位和理想输出湍流相位在相位振幅分布和图像细节方面都高度吻合。而且提取效果并没有随湍流强度的变化而出现波动, 从而证明了基于深度 CNN 提取受湍流影响高斯光束的湍流相位这一方法是十分有效的, 并且还原效果并没有随着湍流强度的增强而出现显著恶化, 证明了该方法的普遍适用性。

6、同GS算法的对比

GS 算法提取湍流相位的第一步是对初始高斯光束做快速傅里叶变换 (fast Fourier transform, FFT), 以确定相应光场函数的像平面分布. 然后其频域振幅由携带湍流相位的高斯光束的频域振幅代替。 接着经过快速傅里叶逆变换(inverse fast Fouriertransform, IFFT), 这时的空域振幅再用入射高斯光振幅代替, 最后对其作 FFT。

CNN 与 GS 算法提取湍流相位效果对比如下所示，(a), (b), (c) 受湍流强度为 影响的高斯光束; (d), (e), (f) 实际湍流相位; (g), (h), (i) 基于 CNN 模型提取的湍流相位; (j), (k), (l) GS 算法提取的湍流相位 。

利用 GS 算法提取的湍流相位无论在相位振幅分 布 还 是 图 像 细 节 方 面 都 远 不 如 基 于 深 度CNN 模型输出的结果。

在时间对比上也是CNN模型占优。训练好的 CNN 模型预测一个湍流相位所耗时间在毫秒量级, 并且几乎与湍流强度无关。而 GS 算法一般都需要进行 70 次的迭代才可以得到比较好的输出 , 这意味着对于每一个相位的预测都需要花费 0.4 s 左右的时间, 其所花费的时间大约是 CNN的100 倍。

优化方向：

1、增加网络层数

2、稀疏化编码

二、CNN识别手写数字

1、两个性质

1、平移不变性（translation invariance）：不管检测对象出现在图像中的哪个位置，神经网络的前面几层应该对相同的图像区域具有相似的反应，即为“平移不变性”。

平移不变性。 这意味着检测对象在输入X中的平移，应该仅导致隐藏表示H中的平移。即V和U实际上不依赖（i,j）的值，也就是说[V]i,j,a,b=[V]a,b，并且U作为一个常数。即H的定义为以下：

2、局部性（locality）：神经网络的前面几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系，这就是“局部性”原则。最终，可以聚合这些局部特征，以在整个图像级别进行预测。

为了收集用来训练参数[H]i,j的相关信息，我们不应偏离到距(i,j)很远的地方。这意味着在|a|>Δ或|b|>Δ的范围之外，我们可以设置[V]a,b=0。因此，我们可以将[H]i,j重写为

 

卷积是当把一个函数“翻转”并移位x时，测量f和g之间的重叠。 当为离散对象时，积分就变成求和。例如：对于由索引为Z的、平方可和的、无限维向量集合中抽取的向量，我们得到以下定义：

 

对于二维张量，则为f的索引(a,b)和g的索引(i−a,j−b)上的对应加和：

图像不是二维张量，而是一个由高度、宽度和颜色组成的三维张量，比如包含1024×1024×3个像素。 前两个轴与像素的空间位置有关，而第三个轴可以看作是每个像素的多维表示。输入图像是三维的，即H也应该采用三维张量，可以把隐藏表示H想象为一系列具有二维张量的通道（channel）。 这些通道有时也被称为特征映射（feature maps），因为每个通道都向后续层提供一组空间化的学习特征。 直观上你可以想象在靠近输入的底层，一些通道专门识别边缘，而一些通道专门识别纹理。因此H重写为：

 

2、图像卷积

在CNN识别手写数字模型中，神经网络主要为8层，2个卷积层、2个池化层、2个全连接层，3个全连接层，1个扁平化层。卷积核设大小为3×3，输入向量大小为28×28，通道数为1。激活函数为ReLU函数。池化层窗口大小设置为2✖2。在全连接层进行降维，张量大小从120->84->10-，之后进行输出。神经网络代码如下：

model = tf.keras.models.Sequential([
    # 第一层卷积层
    tf.keras.layers.Conv2D(filters=6, kernel_size=(5,5), padding='valid', activation=tf.nn.relu, input_shape=(28,28,1)),
    # 第一池化层
    tf.keras.layers.AveragePooling2D(pool_size=(2,2), strides=(2,2), padding='same'),
    # 第二卷积层
    tf.keras.layers.Conv2D(filters=16, kernel_size=(5,5), padding='valid', activation=tf.nn.relu),
    # 第二池化层
    tf.keras.layers.AveragePooling2D(pool_size=(2,2), strides=(2,2), padding='same'),
    # 扁平化层，将多维数据转换为一维数据。
    tf.keras.layers.Flatten(),
    # 全连接层
    tf.keras.layers.Dense(units=120, activation=tf.nn.relu),
    # 全连接层
    tf.keras.layers.Dense(units=84, activation=tf.nn.relu),
    # 输出层，全连接
    tf.keras.layers.Dense(units=10, activation=tf.nn.softmax)
])

加载MNIST数据集

def load_data_mnist(batch_size, resize=None):   #@save

    mnist_train, mnist_test = tf.keras.datasets.mnist.load_data()
    process = lambda X, y: (tf.expand_dims(X, axis=3) / 255,
                            tf.cast(y, dtype='int32'))
    resize_fn = lambda X, y: (
        tf.image.resize_with_pad(X, resize, resize) if resize else X, y)
    return (
        tf.data.Dataset.from_tensor_slices(process(*mnist_train)).batch(
            batch_size).shuffle(len(mnist_train[0])).map(resize_fn),
        tf.data.Dataset.from_tensor_slices(process(*mnist_test)).batch(
            batch_size).map(resize_fn))


train_iter, test_iter = load_data_mnist(128)

优化器设置为内置的随机梯度下降，学习率为0.1，损失函数为交叉熵，训练10次

model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1), loss=tf.losses.sparse_categorical_crossentropy, metrics = ['accuracy'])
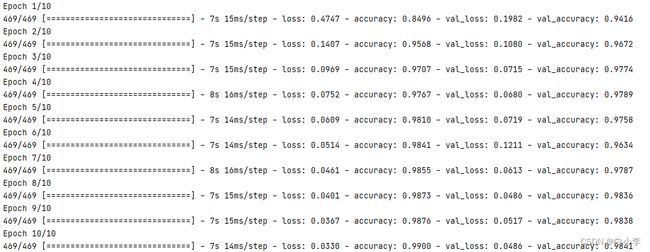
result = model.fit(train_iter, epochs=10, validation_data=test_iter)
model.save('MNIST.h5')
print(result.history)

可视化展示

import tensorflow as tf
import matplotlib.pyplot as plt
import cv2

(_, _), (x, y) = tf.keras.datasets.mnist.load_data()
model = tf.keras.models.load_model('MNIST.h5')
image = cv2.imread('num9.png', cv2.IMREAD_GRAYSCALE)
image = cv2.resize(image, (28, 28)) / 255
image = 1 - image
# print(image)
# print(x[0] / 255)

out = model.predict(tf.reshape(tf.constant(image, dtype=float), (1, 28, 28, 1)))
print(out[0].argmax())
plt.imshow(image)
plt.show()

最后训练跑出来的结果。由此可见随着次数的增加，损失值Loss逐步降低，准确值Acc是一步步升高的。

 

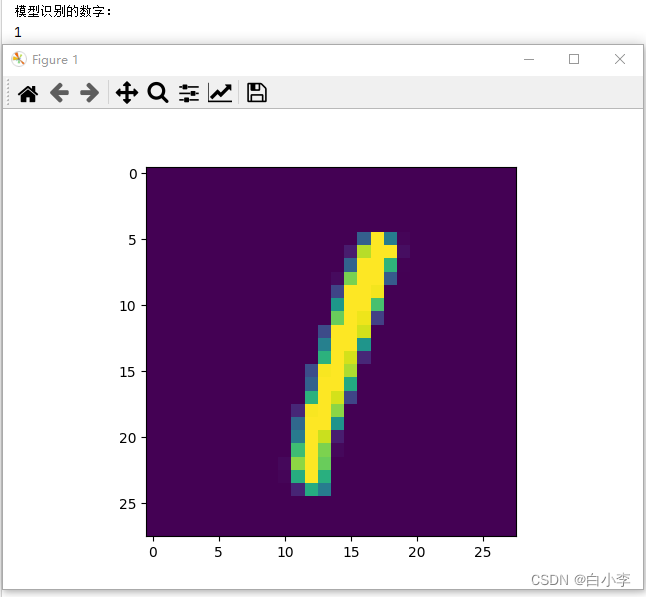
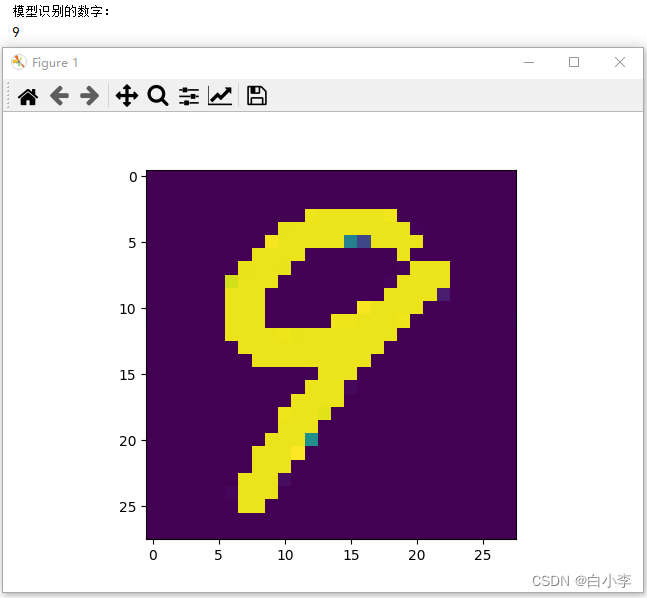
 在可视化展示中，测试了MNIST数据集和自己手写的数据图片。

MNIST数据集

 自己手写的数字图片：

总结

本周阅读了《基于深度卷积神经网络的大气湍流相位提取》论文，学习了卷积神经网络在大气方面的应用相较于其它方法的不同和优势，以及对于卷积数学原理方面进行了学习。同时对于CNN识别手写数字进行了代码复现。