CF1552C Maximize the Intersections 题解 思维

Maximize the Intersections

传送门

On a circle lie $2n$ distinct points, with the following property: however you choose $3$ chords that connect $3$ disjoint pairs of points, no point strictly inside the circle belongs to all $3$ chords. The points are numbered $1,2,\dots ,2n$ in clockwise order.

Initially, $k$ chords connect $k$ pairs of points, in such a way that all the $2k$ endpoints of these chords are distinct.

You want to draw $n-k$ additional chords that connect the remaining $2(n-k)$ points (each point must be an endpoint of exactly one chord).

In the end, let $x$ be the total number of intersections among all $n$ chords. Compute the maximum value that $x$ can attain if you choose the $n-k$ chords optimally.

Note that the exact position of the $2n$ points is not relevant, as long as the property stated in the first paragraph holds.

Input

The first line contains a single integer $t$ ($1\le t\le 100$) — the number of test cases. Then $t$ test cases follow.

The first line of each test case contains two integers $n$ and $k$ ($1\le n\le 100$, $0\le k\le n$) — half the number of points and the number of chords initially drawn.

Then $k$ lines follow. The $i$-th of them contains two integers $x_i$ and $y_i$ ($1\le x_i,y_i\le 2n$, $x_i\ne y_i$) — the endpoints of the $i$-th chord. It is guaranteed that the $2k$ numbers $x_1,y_1,x_2,y_2,\dots ,x_k,y_k$ are all distinct.

Output

For each test case, output the maximum number of intersections that can be obtained by drawing $n-k$ additional chords.

Example

input

4
4 2
8 2
1 5
1 1
2 1
2 0
10 6
14 6
2 20
9 10
13 18
15 12
11 7

output

4
0
1
14

Note

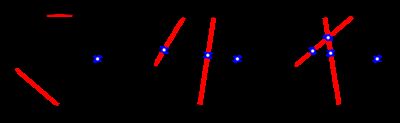
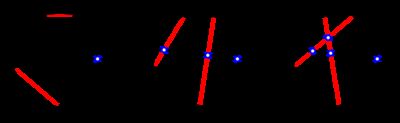
In the first test case, there are three ways to draw the $2$ additional chords, shown below (black chords are the ones initially drawn, while red chords are the new ones):

We see that the third way gives the maximum number of intersections, namely $4$.

In the second test case, there are no more chords to draw. Of course, with only one chord present there are no intersections.

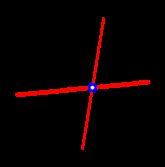
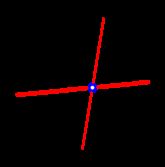
In the third test case, we can make at most one intersection by drawing chords $1-3$ and $2-4$, as shown below:

题目翻译

在一个圆上有 $2n$ 个不同的点，这些点具有以下性质：无论你如何选择连接 $3$ 对不相交点的 $3$ 条弦，严格意义上，圆内没有点属于所有 $3$ 条弦。这些点按顺时针顺序编号为 $1,2,\dots ,2n$ 。

最初， $k$ 条弦连接 $k$ 对点，使得这些弦的所有 $2k$ 端点都是不同的。

您希望绘制连接其余 $2(n-k)$ 个点的 $n-k$ 条额外的弦（每个点必须是一条弦的端点）。

最后，假设 $x$ 是所有 $n$ 条弦的交点总数。计算如果最优化地选择 $n-k$ 条弦， $x$ 所能达到的最大值。

注意，只要第一段所述的性质成立， $2n$ 点的具体位置并不重要。

输入格式

第一行包含一个整数 $t$ ( $1\le t\le 100$ ) - 测试用例的数量。然后是 $t$ 个测试用例。

每个测试用例的第一行包含两个整数 $n$ 和 $k$ （ $1\le n\le 100$ ， $0\le k\le n$ ）–最初绘制的点数和和弦数的一半。

然后是 $k$ 行。其中的 $i$ /th包含两个整数 $x_i$ 和 $y_i$ （ $1\le x_i,y_i\le 2n$ ， $x_i\ne y_i$ ）-- $i$ /th弦的端点。可以保证 $2k$ 个数字 $x_1,y_1,x_2,y_2,\dots ,x_k,y_k$ 都是不同的。

输出格式

对于每个测试用例，输出绘制 $n-k$ 条额外弦线所能获得的最大交叉点数量。

提示

在第一个测试案例中，有三种绘制 $2$ 附加和弦的方法，如下图所示（黑色和弦为最初绘制的和弦，红色和弦为新绘制的和弦）：

我们可以看到，第三种方法得到的交点数最多，即 $4$ 。

在第二个测试案例中，没有更多的弦需要绘制。当然，如果只有一条弦，就没有交点。

在第三种测试情况中，我们最多可以通过绘制弦 $1-3$ 和 $2-4$ 来得到一个交点，如下图所示：

$以上来自$CodeForces$，翻译：DeepL$

解题思路

• 考虑新连上去的弦的相交。把这些点重新编号为 $1$ 至 $2(n-k)$，此时，将 $i$ 和 $i+n-k$ 相连就是最优解的了。
  为什么呢？因为在此时无论交换哪两个端点都只能使两条弦变得不相交，从而减少交点。
• 考虑这些弦和原来已有的弦的相交。可以发现，这样的安排也是最优的，因为交换同样不能让它有更多的交点。

构造好后，判断交点即可。

AC Code

#include
using namespace std;
#define int long long
int n, k;
int ans;
inline bool check_and_done(pair<int, int> x, pair<int, int> y);
inline void solve();
inline void work() {
	int T;
	cin >> T;
	while (T--)solve();
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	work();
}
inline bool check_and_done(pair<int, int> x, pair<int, int> y) {
	if (x.first > y.first)swap(x, y);
	return x.second > y.first && x.second < y.second;
}
inline void solve() {
	cin >> n >> k;
	vector<pair<int, int> > storage_member;
	vector<bool> vis(2 * n + 1);
	for (int i = 1, x, y; i <= k; i++) {
		cin >> x >> y;
		if (x > y)swap(x, y);
		storage_member.push_back(make_pair(x, y));
		vis[x] = vis[y] = 1;
	}
	vector<int> unvis_member_temp;
	for (int i = 1; i <= 2 * n; i++)if (!vis[i])unvis_member_temp.push_back(i);
	for (int i = 0; i < n - k; i++)storage_member.push_back(make_pair(unvis_member_temp[i], unvis_member_temp[i + n - k]));
	ans = 0;
	for (int i = 0; i < n; i++)for (int j = i + 1; j < n; j++)if (check_and_done(storage_member[i], storage_member[j]))ans += 1;
	cout << ans << endl;
}

温馨提示

此题洛谷评分：$普及+/提高$，是不是非常简单？

粉丝福利

还在为 $CodeForces$，全英文而苦恼吗？还在为洛谷的()()翻译而苦恼吗？翻译插件这不就来了吗。